Введение
Настоящая работа является продолжением исследований автора, которые наиболее полно изложены в работе [1]. Как следует из этой работы (стр.94), лагранжиан F вариационной задачи в пограничном слое ![]() имеет вид
имеет вид
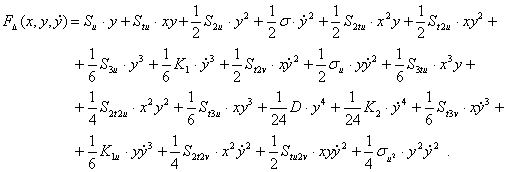 (1)
(1)
В этой формуле константы перед аргументом x, переменными ![]() определяются из постановки задачи и могут быть найдены согласно работам [1, 2].
определяются из постановки задачи и могут быть найдены согласно работам [1, 2].
Уравнение Эйлера—Лагранжа для интегранта ![]() представляется выражением
представляется выражением
![]() (2)
(2)
Начальные условия для нелинейного обыкновенного дифференциального уравнения (ОДУ) второго порядка (2) следующие:
![]() (3)
(3)
Из уравнения (2) и формул (1), (3) следует вид уравнения Эйлера–Лагранжа в пограничном слое:
![]() (4)
(4)
Функции ![]() определяются следующим образом:
определяются следующим образом:
![]()
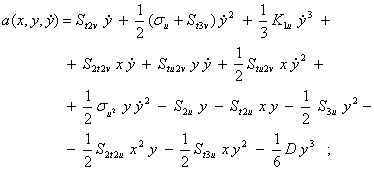
![]()
где
![]()
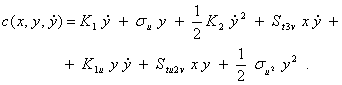
Гомоморфизм
Стандартным образом введем понятие гомоморфизма: каждому элементу и каждому отношению между элементами первой системы соответствует один элемент и одно отношение второй системы (но не наоборот) [3].
Сходство модели с оригиналом всегда неполное. Модель лишь приближенно отражает некоторые свойства оригинала. Причем реальная система может иметь различные гомоморфные ей модели [4].
Часто математические задачи, возникающие на основе различных математических моделей, явлений бывают одинаковыми. Приведем примеры: основная задача линейного программирования, обыкновенное дифференциальное уравнение колебательной системы, как и уравнение Эйлера-Лагранжа для пограничного слоя (4), отражают ситуации различной природы. Это дает обоснование считать эти различные математические модели гомоморфными по отношению к математическим задачам, к которым эти модели приводятся. Такие типичные математические задачи исследуются как самостоятельный объект, абстрагируясь от изучаемых явлений.
Уравнению (4) соответствуют следующие задачи [1]: моделирование движения тела переменной массы, моделирование задач теории оптимальных аэродинамических форм вблизи особой точки, представление плоских кривых вблизи точки возврата.
Гомоморфизм является фундаментальным теоретическим обоснованием моделирования.
На всех этапах исследования математическая теория, физический и численный эксперимент за компьютером должны применяться совместно и согласованно.
Структура алгебры уравнения
Согласно формуле (1) введем множество [5]
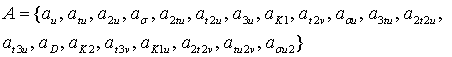 , (5)
, (5)
где:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . (6)
. (6)
Введем обозначения для констант:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() . (7)
. (7)
На основании формул (1), (5) – (7) определим множество B следующей формулой:
![]() .
.
В этой формуле индекс ζ принимает значения индексов формул (6), (7).
Таким образом, построили алгебру [6] ![]() типа (2,1), где «+» – бинарная операция [7], «-» – унарная операция [6,7].
типа (2,1), где «+» – бинарная операция [7], «-» – унарная операция [6,7].
СПИСОК ЛИТЕРАТУРЫ:
- Святсков В.А. Уравнение Эйлера-Лагранжа в пограничном слое и его приложения. – Чебоксары: ЧГПУ, 2000. – 165с.
- Святсков В.А. Исследование первых интегралов уравнения Эйлера–Лагранжа в пограничном слое // Известия РАЕН. Дифференциальные уравнения. Рязань: Изд-во РГПУ, 2001. №4. С. 85-95.
- Лопатников Л.И. Экономико-матема-тический словарь. – М.: Наука, 1987. – 509 с.
- Святсков В.А. О гомоморфизме математических моделей // Современные проблемы науки и образования. М.: Изд-во РАЕ, 2006. №1. С.91-92.
- Святсков В.А. Структура алгебры элементов уравнения Эйлера–Лагранжа для пограничного слоя. // Инновации в образовательном процессе: Сборник трудов Межрегиональной научно-практической конференции. – М.: Изд-во МГОУ, 2007. – Вып.5. - С.193-194.
- Матрос Д.Ш., Поднебесова Г.Б. Элементы абстрактной и компьютерной алгебры. – М.: Изд.центр «Академия», 2004. – 240 с.
- Воеводин В.В., Воеводин Вл. В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. – СПб.: БХВ-Петербург, 2006. – 544 с.



