Система координат выбирается так, что ось z направлена вертикально вверх, а плоскость z = 0 совпадает с поверхностью раздела свободной жидкости и пористой среды, насыщенной жидкостью. Толщины плоских слоев пористой среды и свободной жидкости равны h1 и h2 соответственно. Величины, относящиеся к насыщенной пористой среде, обозначим индексом 1, а к свободной жидкости – 2.
Уравнения движения жидкости в пористой среде запишем в виде [1, 2]
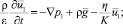
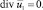 (1)
(1)
Здесь ? – пористость матрицы; ?, ? – плотность и динамическая вязкость жидкости; K – коэффициент проницаемости; 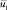 – макроскопическая скорость фильтрации; p1 – давление;
– макроскопическая скорость фильтрации; p1 – давление; 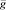 – ускорение свободного падения.
– ускорение свободного падения.
Потенциал скорости 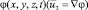 в слое свободной жидкости удовлетворяет уравнению Лапласа [2]
в слое свободной жидкости удовлетворяет уравнению Лапласа [2]
?? = 0. (2)
Применяя к первому уравнению (1) операцию rot rot и проецируя получившееся уравнение на ось z, получим уравнение для вертикальной компоненты скорости u1z
 (3)
(3)
Граничные условия на поверхностях раздела имеют вид (1), (4)
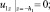
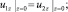 (4)
(4)
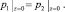
При 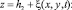
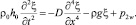 (4?)
(4?)
Здесь ? – смещение точек пластины в вертикальном направлении; 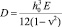 – цилиндрическая жесткость пластины; ?0 – плотность материала пластины; h0 – толщина пластины; E – модуль Юнга; ? – коэффициент Пуассона.
– цилиндрическая жесткость пластины; ?0 – плотность материала пластины; h0 – толщина пластины; E – модуль Юнга; ? – коэффициент Пуассона.
Первое из условий (4) – это условие непротекания на твердой стенке, ограничивающей снизу пористую среду; второе – условие непрерывности расхода на границе раздела жидкость – пористая среда, насыщенная жидкостью; третье – непрерывность давления на этой же границе; четвертое условие является следствием непрерывности давления на свободной возмущенной поверхности слоя жидкости с учетом линеаризованного интеграла Кош – Лагранжа [3] и кинематического условия
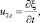
где ?(x, y, t) – смещение точек свободной поверхности в вертикальном направлении.
Решение уравнений (2), (3) с граничными условиями (4) и (4?) ищем в виде
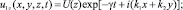 (5)
(5)
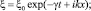
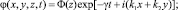
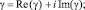
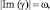
где k1, k2 – вещественные волновые числа, характеризующие периодичность волновых решений (5) по направлениям x и y; ? – частота колебаний; Re(?) = ? – декремент затухания колебаний.
Подставляя (5) в (2), (3), находим
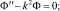 (6)
(6)
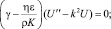
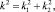
где штрих означает дифференцирование по z.
Граничные условия (4) и (4?) для амплитуд U(x), ?(z) имеют вид
U(z) = 0 (z = –h1); U(z) = ??(z) (z = 0); (7)
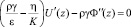 (z = 0);
(z = 0);
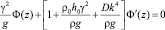 (z = h2).
(z = h2).
Решением системы дифференциальных уравнений (6) являются функции
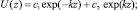 (8)
(8)
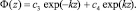
Граничные условия (7) с учетом (8) приводят к однородной системе алгебраических уравнений
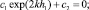
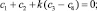 (9)
(9)
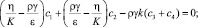
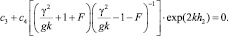
Приравнивая определитель системы (9) к нулю, находим дисперсионное уравнение для поверхностных волн
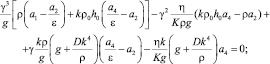 (10)
(10)
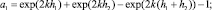
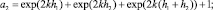
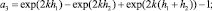
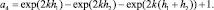
Уравнение (10) кубическое относительно ? с действительными коэффициентами, которое может быть приведено к «неполному» кубическому уравнению [5]. Запишем для этого уравнение (10) в виде
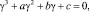 (11)
(11)
где коэффициенты a, b, c – действительные числа, причем
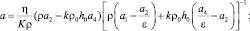
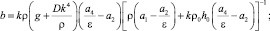 (12)
(12)
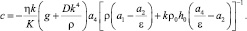
Величину ? представим в виде 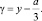 Тогда получим уравнение относительно неизвестного y, которое не содержит квадрата этого неизвестного:
Тогда получим уравнение относительно неизвестного y, которое не содержит квадрата этого неизвестного:
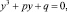 (13)
(13)
где 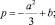
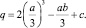
Выражение
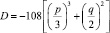 (14)
(14)
называется дискриминантом уравнения (13). При условии D < 0 в формуле Кардано [5] под знаком каждого из кубичных радикалов оказывается действительное число. Кубический корень из действительного числа имеет одно действительное и два комплексно-сопряженных числа. В этом случае существует колебательное движение жидкости.
При условии D ? 0 комплексно-сопряженных корней нет, т.е. в этом случае колебательное движение отсутствует, поэтому этот случай не рассматривается при решении уравнения (13), т.к. при этом волны отсутствуют.
На рис. 1 приведены графики рассчитанных зависимостей декремента затухания ? от волнового числа k при фиксированной толщине пористого слоя h1 = 10 см и толщине тонкой упругой пластины h0 = 0,1 см для различных значений толщины свободной жидкости h2 = 5, 10, 25, 50.
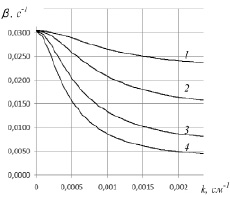
Рис. 1. Зависимость ? от k при h1 = 10 см, h0 = 0,1 см и различных значениях толщины свободной жидкости: 1 – h2 = 5 см; 2 – h2 = 10 см; 3 – h2 = 25 см; 4 – h2 = 50 см
Из рис. 1 видно, что при увеличении волнового числа k при заданном значении h2 модуль декремента затухания уменьшается, т.е. более длинные волны затухают быстрее коротких.
На рис. 2 приведены графики рассчитанных зависимостей частоты ? от волнового числа k при фиксированной толщине пористого слоя h1 = 10 см и толщине тонкой упругой пластины h0 = 0,1 см для различных значений толщины свободной жидкости h2 = 5, 10, 25, 50.
Из рис. 2 видно, что при увеличении волнового числа k при заданном значении частота увеличивается.
На рис. 3 приведены графики рассчитанных зависимостей декремента затухания ? от волнового числа k при фиксированной толщине пористого слоя h2 = 10 см и толщине тонкой упругой пластины h0 = 0,1 см для различных значений толщины свободной жидкости h1 = 5, 10, 25, 50.
Из рис. 3 видно, что при увеличении волнового числа k при заданном значении h1 модуль декремента затухания увеличивается, т.е. более короткие волны затухают быстрее длинных.
На рис. 4 приведены графики рассчитанных зависимостей частоты ? от волнового числа k при фиксированной толщине пористого слоя h2 = 10 см и толщине тонкой упругой пластины h0 = 0,1 см для различных значений толщины свободной жидкости h1 = 5, 10, 25, 50.
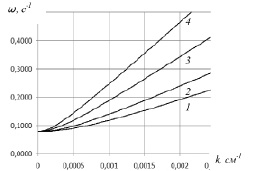
Рис. 2. Зависимость ? от k при h1 = 10 см, h0 = 0,1 см и различных значениях толщины свободной жидкости: 1 – h2 = 5 см; 2 – h2 = 10 см; 3 – h2 = 25 см; 4 – h2 = 50 см
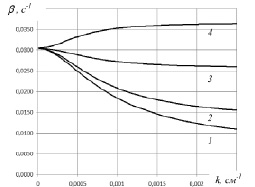
Рис. 3. Зависимость ? от k при h2 = 10 см, h0 = 0,1 см и различных значениях толщины свободной жидкости: 1 – h1 = 5 см; 2 – h1 = 10 см; 3 – h1 = 25 см; 4 – h1 = 50 см
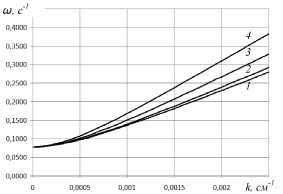
Рис. 4. Зависимость ? от k при h2 = 10 см, h0 = 0,1 см и различных значениях толщины свободной жидкости: 1 – h1 = 5 см; 2 – h1 = 10 см; 3 – h1 = 25 см; 4 – h1 = 50 см
Из рис. 4 видно, что при увеличении волнового числа k при заданном значении h1 частота увеличивается.
Таким образом, исследовано распространение поверхностных волн в слое жидкости, покрытой тонкой упругой пластиной, находящейся на пористом основании. Получено дисперсионное уравнение распространения волн, построены графики изменения декремента затухания и частоты в зависимости от толщины слоя жидкости и пористого основания.
Работа выполнена в рамках гранта на проведение научно-исследовательских работ по приоритетным направлениям научной деятельности вузов-партнёров по сетевому взаимодействию (ФГБОУ ВПО ЧГПУ и МордГПИ) по теме: «Математическое моделирование поверхностных волн в средах, взаимодействующих с магнитным и электрическим полями».
Рецензенты:
Свешников В.К., д.т.н., профессор кафедры физики и методики обучения физике, ФГБОУ ВПО «Мордовский государственный педагогический институт имени М.Е. Евсевьева», г. Саранск;
Тактаров Н.Г., д.ф.-м.н., профессор кафедры математики и методики обучения математике, ФГБОУ ВПО «Мордовский государственный педагогический институт имени М.Е. Евсевьева», г. Саранск.



