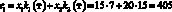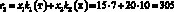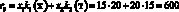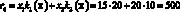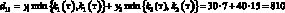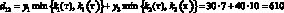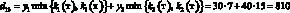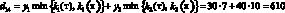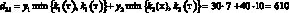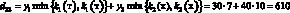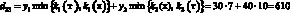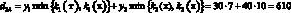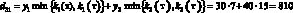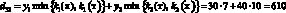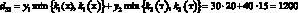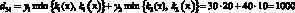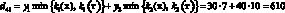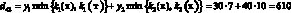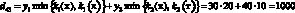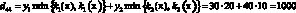Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

На современном этапе экономики аптечного рынка наблюдается значительный рост конкуренции фармацевтических фирм, который вызвал к жизни интенсивное развитие различных аспектов их функционирования [1, 2, 4]. В деятельность фармацевтических фирм внедряется маркетинговая информация об изучении спроса и управлении рынком лекарственных средств, новые рекламные проекты, разработка самостоятельной ценовой политики, ориентированной не только на прибыль, но и на успешное выполнение социальной функции фирмы по обеспечению населения качественными и доступными по цене лекарственными препаратами, расширение сервисных услуг населению и др. [6].

В данной статье анонсируются результаты по моделированию производства и реализации лекарственных препаратов фармацевтической фирмы на основе применения теоретико-игрового аппарата.

Задача

Фирма Лайффарма производит медикаменты. Спрос на лекарственные препараты в большинстве случаев изменяется в зависимости от сезонного периода. В данной задаче будем рассматривать два таких периода: осенне-зимний и весенне-летний.

Сезонность в теории спроса определяется как календарно зависимое циклическое изменение спроса [5]. Точнее, если в результате анализа о продажах не менее чем за три года колебания спроса постоянны в определенные периоды года и составляют не менее 20 % объема продаж, то это свидетельствует о наличии сезонности спроса на этот товар. В данной статье мы употребляем «сезонность» в более широком обиходном смысле для обозначения особенностей поведения рынка, привязанных к двум временным периодам года.

Увеличение спроса в осенне-зимний период подъема респираторных, инфекционных заболеваний и гриппа приходится на противовирусные, анальгезирующие, жаропонижающие и противовоспалительные препараты, а также антибиотики.

В весенне-летний период обострения хронических заболеваний желудочно-кишечного тракта, сердечно-сосудистых заболеваний, гипертонии, вегето-сосудистой дистонии, аллергии приводят к повышению спроса на лекарства для лечения дисбактериоза, противомикробные, анацидные, сердечно-сосудистые и антигистаминные препараты.

Препараты, на которые увеличивается спрос в осенне-зимний и весенне-летний период, будем считать препаратами соответственно первой и второй группы.

Затраты на изготовление 1 условного препарата (уп) первой и второй группы составляют соответственно 15 и 20 условных денежных единиц (уде).

По данным наблюдений за несколько последних лет службой маркетинга фирмы установлено, что она может реализовать в течение осенне-зимнего периода в условиях теплой и холодной погоды соответственно 7 тыс. и 20 тыс. уп, а в течение весенне-летнего периода в условиях теплой и холодной погоды соответственно 15 тыс. и 10 тыс. уп.

Анализ климатических данных, выполненный в Гидрометцентре России, позволяет сделать вывод о том, что в краткосрочный период вероятности П1 (тт) – теплой погоды в оба периода; П2(тх) – теплой погоды в осенне-зимний период и холодной в весенне-летний, П3(хт) – холодной погоды в осенне-зимний период и теплой в весенне-летний; П4(хх) – холодной погоды в оба периода колеблются соответственно в пределах

0,20 < q1 <0,31; 0,15 < q2 < 0,36;

0,10 < q3 < 0,75 и 0,15 < q4 < 0,40. (1)

При определении количества производимых лекарственных препаратов, предназначенных для реализации в последующие осенне-зимний и весенне-летний периоды, фирма, учитывая долгосрочные прогнозы погоды (от 10 суток до 3 месяцев), руководствуется спросом для наиболее полного его удовлетворения и одной из четырех обладающих ею стратегий, исходя из следующих своих предположений: A1(тт) – будет теплая погода в оба периода; A2(тх) – теплая погода в осенне-зимний период и холодная в весенне-летний период; A3(хт) – холодная погода в осенне-зимний период и теплая в весенне-летний период; A4(хх) – холодная погода в оба периода. По результатам анализа за последние годы предположения фирмы A1(тт), A2(тх), A3(хт), A4(хх) оправдываются соответственно с вероятностями p1 = 0,35; p2 = 0,30; p3 = 0,15; p4 = 0,20.

В связи с возможными изменениями погоды ставится задача определения фирмой вероятностей состояний погоды П1(тт), П2(тх), П3(хт), П4(хх) из заданных промежутков, оптимальных в смысле наибольшей средней прибыли от реализации лекарственных препаратов при цене продажи 30 уде за 1 уп первой группы и 40 уде за 1 уп второй группы.

Математическая модель – «Игра с природой»

В теории и на практике многократного принятия финансово-экономических решений в условиях риска часто пользуются математической моделью «Игра с природой» ([3], гл. 1), в которой предполагается известным вектор q = (q1, q2, ..., qn), n ? 2, вероятностей qj состояний природы Пj, удовлетворяющих условиям

qj > 0, j = 1, 2, ..., n, 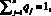(2)

а эффективность смешанных стратегий понимается в смысле выигрыш-критерия Байеса ([3], гл. 2, §§ 2.1, 2.2). Предположение о положительности вероятностей qj, j = 1, 2, ..., n, состояний природы не умаляет общности, поскольку состояние природы с нулевой вероятностью не играет существенной роли в анализе ситуации и потому его можно исключить из рассмотрения.

Напомним определение выигрыш-критерия Байеса и некоторые связанные с ним понятия.

Пусть A – игрок в игре с природой, осознанно принимающий решения о выборе одной из возможных чистых стратегий A1, A2, ..., Am, m ? 2. Смешанной стратегией P = (p1, p2, ..., pm) игрока A называется действие, состоящее в случайном выборе чистой стратегии Ai с вероятностью pi ? 0, i = 1, 2, ..., m, где 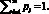Через aij обозначим выигрыши игрока A в игровой ситуации (Ai, Пj), когда он выбирает чистую стратегию Ai, а природа находится в состоянии Пj. Массив выигрышей aij, i = 1, 2, ..., m; j = 1, 2, ..., n, представляется в виде матрицы выигрышей (платежной матрицы)

Через

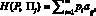j = 1, 2, ..., n

обозначим выигрыш игрока A в игровой ситуации (P, ?j), когда игрок A действует в соответствии со смешанной стратегией P = (p1, p2, ..., pm), а природа находится в состоянии ?j. Показатель эффективности смешанной стратегии P определяется по формуле

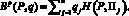[1].

Пусть Bp(P) – множество показателей эффективности Bp(P, q) фиксированной смешанной стратегии P при всевозможных векторах вероятностей состояний природы q = (q1, q2, ..., qn), удовлетворяющих условиям (2).

Так как показатель эффективности Bp(P, q) является выпуклой комбинацией выигрышей H(P, ?j), j = 1, 2, ..., n, с коэффициентами qj, j = 1, 2, ..., n, то

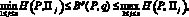(3)

при любом векторе q вероятностей состояний природы, удовлетворяющем условиям (2).

Теорема 1. Для того чтобы при любом векторе вероятностей состояний природы q = (q1, q2, ..., qn), удовлетворяющем условиям (2), левое (правое) неравенство (3) было равенством

;

,

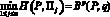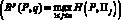необходимо и достаточно, чтобы все выигрыши при стратегии P и при каждом состоянии природы равнялись между собой:

H(P, ?1) = H(P, ?2) = ... H(P, ?n).

Из неравенства (3) и теоремы 1 непосредственно вытекает следующее утверждение.

Теорема 2. Для справедливости строгого неравенства

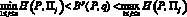
при любом векторе вероятностей состояний природы q = (q1, q2, ..., qn), удовлетворяющем условиям (2), необходимо и достаточно, чтобы не все выигрыши при стратегии P были равны между собой.

Теорема 3. Пусть не все выигрыши при смешанной стратегии P равны между собой и ? > 0 – произвольное число. Пусть

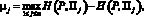
j = 1, 2, ..., n; (4)

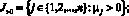
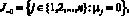(5)

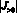где и 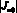 – количества номеров соответственно множеств 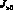и ,

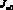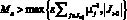(6)

– произвольное число.

Тогда вектор 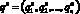с координатами

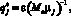при ,

и

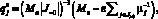
при 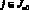, (7)

может служить вектором вероятностей состояний природы и показатель эффективности Bp(P, q(?)) стратегии P будет отличаться от верхней границы 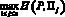множества Bp(P) меньше, чем на ?:

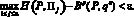
Следствие 1. В условиях теоремы 3 справедливо неравенство

,

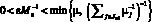где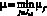

Следствие 2. Если в условиях теоремы 3 число ? удовлетворяет неравенству

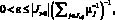
то число M? можно выбрать независящим от ?, например, следующим образом:

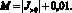(8)

Следствие 3. Неравенство

,

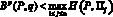справедливое при любом векторе вероятностей состояний природы q = (q1, q2, ..., qn), удовлетворяющем условиям (2), по достаточной части теоремы 2, когда не все выигрыши при стратегии P равны между собой, является точным, т.е. его правая часть представляет собой точную верхнюю границу множества Bp(P):

.

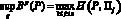Следствие 4. Если не все выигрыши при стратегии P равны между собой, то

,

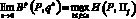где координаты вектора 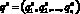определяются равенствами (7) с использованием (4), (5) и (6).

Следствие 5. В условиях теоремы 3 и следствия 2 показатель Bp(P, q(?)) эффективности смешанной стратегии P как функция от 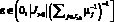монотонно возрастает при ? ? 0.

Предположим, что в игре с природой известны не вероятности qj, j = 1, 2, ..., n, состояний природы ?j, j = 1, 2, ..., n, а лишь промежутки их изменений для каждого состояния природы: 0 < ?j ? qj ? ?j ? 1, j = 1, 2, ..., n. Пусть M, ?j, j = 1, 2, ..., n, и 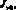 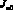 – определяется соответственно равенствами (8), (4) и (5). Рассмотрим множества

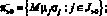
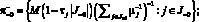
?– = {0};

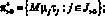
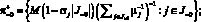
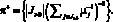
Пусть ? – наибольший элемент объединения

: ,

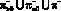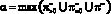а ? – наименьший элемент объединения

:

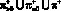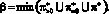
Теорема 4. Если в условиях теоремы 3 справедливо неравенство ? ? ?, то для любого ? ? [?, ?] координаты вектора 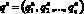, определяемые формулой (7), являются вероятностями состояний природы и принадлежат соответствующим промежуткам [?j, ?j], а показатель эффективности Bp(P, q(?)) отличается от верхней границы 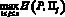множества Bp(P) меньше, чем на ?.

Аналогичные результаты можно получить и для нижней границы .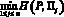

Теоретико-игровая формализация задачи

Для удобства обозрения все данные в условии задачи сведем в табл. 1.

Таблица 1

Таблица 2

Издержки на производство уп при выборе фирмой чистых стратегий

Таблица 3

Доход от продажи уп при выборе фирмой чистых стратегий и при нахождении природы в своих состояниях

Для анализа задачи в качестве модели используем игру с природой, в которой роль игрока A исполняет фирма Лайффарма, а природой является погода, находящаяся в одном из своих состояний: ?1(тт), ?2(тх), ?3(хт), ?4(хх). Игрок A обладает четырьмя чистыми стратегиями A1(тт), A2(тх), A3(хт), A4(хх). В следующей таблице указаны формулы и результаты вычисления расходов на производство уп при выборе фирмой своих чистых стратегий.

В следующей таблице указаны формулы и результаты подсчета дохода от продажи уп при выборе фирмой чистых стратегий и при нахождении природы в своих состояниях.

Например, доход d12 в случае, когда фирма при производстве продукции руководствуется стратегией A1(тт), а погода находится в состоянии ?2(тх), подсчитывается следующим образом. При такой стратегии фирма считает, что погода в оба сезона будет теплой и потому (табл. 1) производит k1(т) = 7 тыс. уп 1-й группы и k2(т) = 15 тыс. уп 2-й группы. При состоянии ?2(тх) погода оказалась теплой в осенне-зимний период и, следовательно, (табл. 1), все k1(т) = 7 тыс. уп будут реализованы, а в весенне-летний период погода оказалась холодной, и, следовательно (табл. 1), из k2(т) = 15 тыс. уп будут реализованы лишь k2(х) = 10 тыс. Таким образом, доход

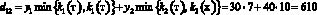
(табл. 3, вторая строчка).

Роль выигрышей в модели будет играть прибыль, равная разности дохода и издержек, в соответствующих игровых ситуациях, когда игрок A выбирает одну из возможных чистых стратегий A1(тт), A2(тх), A3(хт), A4(хх), а природа находится в одном из своих состояний ?1(тт), ?2(тх), ?3(хт), ?4(хх). Подсчитанные выигрыши составляют элементы платежной матрицы

Решение задачи

По условиям задачи смешанная стратегия P = (0,30; 0,35; 0,15; 0,20) является для фирмы приемлемой. Подсчитаем выигрыши 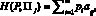j = 1, 2, 3, 4, при этой смешанной стратегии:

H(P, ?1) = 281,75; H(P, ?2) = 191,75;

H(P, ?3) = 418,25; H(P, ?4) = 328,25. (9)

Отсюда видно, 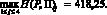Тогда из (9) по формуле (4):

?1 = 136,5; ?2 = 226,5; ?3 = 0; ?4 = 90. (10)

Следовательно, 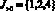, 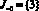и 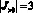, 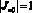. Далее из (10) имеем

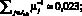
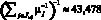
и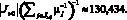

В соответствии со следствием 5 будем предполагать, что 0 < ? < 130,434 и тогда можно считать, что число M = 3,001 не зависит от числа ? в указанных пределах.

Так как левые и правые концы данных промежутков (1): ?1 = 0,20; ?2 = 0,15, ?3 = 0,10, ?4 = 0,15; ?1 = 0,31; ?2 = 0,36; ?3 = 0,75; ?4 = 0,40, то, используя (10), бу дем иметь

M?1?1 = 81,927; M?2?2 = 101,959;

M?4?4 = 40,514;

;

M?1?1 = 126,987; M?2?2 = 244,702;

M?4?4 = 108,036;

Таким образом,

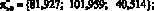
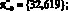?– = {0},

откуда

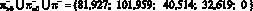
и

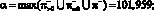
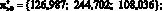
?+ = {117,430}; ?+ = {130,434},

откуда

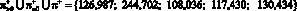
и

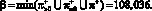
Таким образом, справедливо неравенство ? < ?, означающее, что пересечение промежутков [81,927; 126,987], [101,959; 244,702], [32,619; 117,430], [40,514; 108,036] и (0, 130,434] не пусто и совпадает с отрезком [101,959; 108,036].

Для любого ? ? [101,959; 108,036], используя значения (10) и равенство M? = M = 3,001, найдем по формулам (7) вероятности состояний природы 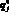, j = 1, 2, 3, 4:

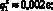
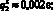
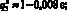
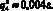(11)

Вероятности (11) обладают свойствами (2) и по теореме 4 принадлежат соответственно заданным промежуткам [0,20; 0;31], [0,15; 0,36], [0,10; 0,75], [0,15; 0,40] их изменения[2], в чем можно убедиться и непосредственно. Например, покажем, что 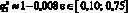. Имеем: 101,959 ? ? ? 108,036. Умножая все части этого двойного неравенства на (–0,008) и прибавляя к каждой из них по 1, получим неравенство 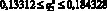, из которого следует требуемое.

Подсчитав по формулам (11) векторы вероятностей состояний природы при ? = 101,959 и ? = 108,036, получим

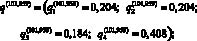
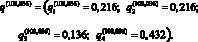
Используя вычисленные выигрыши (9) и векторы вероятностей состояний природы q(101,959) и q(108,036), найдем показатели эффективности Bp(P, q(?)) смешанной стратегии P = (0,30; 0,35; 0,15; 0,20) при ? = 101,959 и ? = 108,036:

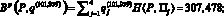
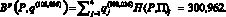
Заключение

Таким образом, при убывании управляющего параметра ? от 108,036 до 101,959 показатель эффективности Bp(P, q(?)) смешанной стратегии P = (0,30; 0,35; 0,15; 0,20) в соответствии со следствием 5 монотонно возрастает от 300,962 до 307,478. Поэтому если фирма Лайффарма будет производить лекарственные препараты в соответствии со стратегией P = (0,30; 0,35; 0,15; 0,20), то при крайне оптимистическом прогнозе фирма может считать, что вектором вероятностей состояний природы является вектор q(101,959), и в этом случае средневзвешенная прибыль, выражаемая показателем Bp(P, q(101,959)) эффективности стратегии P = (0,30; 0,35; 0,15; 0,20), будет наибольшей из возможных, равной 307,478 уде. При крайне пессимистическом подходе фирма в качестве вектора вероятностей состояний природы может выбрать вектор q(108,036), при котором средневзвешенная прибыль Bp(P, q(108,036)) будет наименьшей из возможных, равной 300,962 уде.