Постановка вопроса. Ставится задача построить схему программной локализации (и приближенного вычисления) нулей и экстремумов функций одной и более переменных в произвольной области на плоскости. Аналогичная задача ставится для разностных приближений решений систем обыкновенных дифференциальных уравнений (ОДУ), при этом число уравнений и длина промежутка изменения независимой переменной могут быть произвольными. Помимо того, рассматриваемую схему требуется перенести на вычисление нулей многочленов с учетом их кратности, включая нули характеристического многочлена матрицы. Схему предполагается применить для компьютерного анализа устойчивости по Ляпунову системы ОДУ как в случае асимптотической, так и неасимптотической устойчивости на основе параллельного метода нахождения собственных значений матрицы постоянных коэффициентов системы линейных ОДУ произвольного порядка.
Базовая схема сортировки и локализации экстремумов функции. Пусть вначале требуется локализовать и приближенно вычислить все минимумы действительной функции одной действительной переменной
y = f(x) (1)
на промежутке [x(0), x(N)] в области ее определения. Строится равномерная сетка:
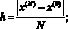x? = x(0) + ?h, ? = 0, 1, ..., N.
На сетке считываются значения функции (1)
c[i] = f(xi–1), i = 1, 2, ..., N. (2)
Элементы массива (2) сортируются. Используется быстрая сортировка, основанная на адресном слиянии двух упорядоченных массивов по матрице сравнений, детально описанная в [3–5]. К выходу сортировки подсоединяется условный оператор, осуществляющий локализацию каждого минимума в окрестности произвольно заданного радиуса ? среди элементов (2), при условии, что ? меньше половины расстояния между любыми двумя соседними минимумами. Такой оператор можно представить соотношением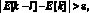 
l = 1, 2, ..., k – 1. Индексы E[k] входных элементов располагаются на выходе в порядке элементов отсортированного массива. Смысл оператора в том, что в ?-окрестности входного элемента с индексом E[k] нет элемента в отсортированном массиве, превосходящего по значению элемент с этим индексом. Данный оператор ниже называется оператором локализации минимума. После локализации минимума выполняется спуск к наименьшему значению в окрестности локализованной точки. Он осуществляется выбором наименьшего значения в сужаемой окрестности c фиксированным числом элементов равномерной сетки, пока не достигается требуемая точность.
Например, все минимумы функции y = sin(x) на [–30, 30] в результате работы программы, листинг которой представлен в [7, 15], примут значения
Достигнутая точность приближения характерна для излагаемого метода.
Инвариантность метода относительно длины промежутка достигается путем смещения базового промежутка с числом узлов N на расстояние, равное его длине. Во избежание ложных экстремумов отсекаются обе границы текущего промежутка, проверка его границ на экстремумы производится с помощью сортировки. Эта сортировка локализует экстремумы по ранее описанной схеме для элементов массива, образуемых значениями функции (1) слева от правой границы и справа от левой границы. В результате достигается инвариантность схемы относительно размеров области поиска экстремумов. По построению схема инвариантна относительно вида функции (2), на которую не накладывается математических ограничений. Функция, в частности, может быть задана таблично, при этом спуск окажется излишним.
Вычисление всех локальных максимумов в области с произвольно заданными границами можно произвести, если условие локализации минимума заменить на условие локализации максимума путем обратного направления просмотра элементов отсортированного массива: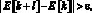 
l = 1, 2, ..., n – k.
Вычисление нулей функции одной действительной переменной. Для локализации и вычисления нулей функции (1) достаточно на вход сортировки подать абсолютные величины ее значений на равномерной сетке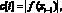 
i = 1, 2, ..., n, и искать минимумы описанным выше способом. Например, та же программа локализует и вычислит все нули многочлена
P = P1?P2?P3,
где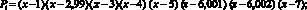 
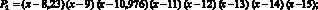
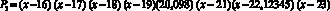
в виде
1.00000000000000000E+0000 0.00000000000000E+0000
3.00000000000000000E+0000 0.00000000000000E+0000
…………………………………………………
2.21234500000000000E+0001 0.00000000000000E+0000
2.30000000000000000E+0001 0.00000000000000E+0000
Схема локализации и вычисления экстремумов функции двух действительных переменных. Для нахождения всех экстремумов действительной функции двух действительных переменных
z = f(x, y) (3)
в области ее определения первоначально задаются текущие промежутки с границами [x(0), x(N)] и [y(0), y(M)]. Внутри ограниченных ими прямоугольников строится равномерная прямоугольная сетка:
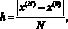x? = x(0) + ?h,
? = 0, 1, ..., N; y? = y(0) + ?h, ? = 0, 1, ..., M.
Для нахождения минимумов функции (3) выполняется проход в направлении оси OY вдоль j-го столбца прямоугольной сетки, во время которого находится минимальное по строкам значение c[j] = min f(xj, yi) (1 ? i ? M), этот минимум заносится на вход сортировки как j-й элемент сортируемого одномерного массива. К выходу процедуры подсоединяется оператор локализации минимума. Спуск к наименьшему значению в окрестности локализованной точки осуществляется с помощью выбора наименьшего значения в сужаемой окрестности c фиксированным числом элементов в сетке, причем по обеим переменным, пока не будет достигнута требуемая точность. Такой спуск повторяется дважды [4] с целью повышения точности приближения. Локализация максимума производится аналогично одномерному случаю.
Таким образом, первоначально изложенная схема переносится на случай функции двух действительных переменных. С ее помощью автоматически программно локализуются и вычисляются экстремумы произвольной функции в произвольной прямоугольной области на плоскости, входящей в область определения функции.
Вычисление нулей функции двух переменных. Нули функции (3) вычисляются по описанной для минимумов схеме, если на вход метода подать
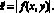(4)
Все локализованные минимумы модуля исследуемой функции будут включать ее нули. Их можно идентифицировать по значению функции. Если других минимумов нет, то будут локализованы и вычислены именно нули в произвольно заданной и зафиксированной области на плоскости. В частности, так вычисляются все нули многочленов с комплексными коэффициентами [1, 13]. Изложенная выше схема отличается от известных построением на основе сортировки, «автоматизмом» и отмеченной инвариантностью программной локализации нулей и экстремумов. В отличие от схем, ориентированных только на вычисление нулей, по изложенной схеме вычисляются как нули, так и произвольные экстремумы в произвольной области на плоскости.
Программной особенностью схемы является ее инвариантность относительно размеров области, не требующая объявления динамических массивов. Схема обладает параллелизмом на основе разбиения области на взаимно независимые фрагменты, а также на основе параллелизма использованных сортировок.
Представленная схема переносится на случай функции трех переменных, но при этом требует существенных затрат машинного времени. По этой причине для трех переменных на персональном компьютере реализована только локализация экстремумов без спуска к локализованному значению. В качестве привязки используется программно вычисляемый минимум (аналогично максимум) этой функции, который вначале берется по двум переменным при фиксировании третьей, а затем по одной переменной при фиксировании двух других. Экстремумы по фиксируемым переменным после их использования в качестве привязок локализуются программно с помощью описанной выше схемы.
Вычисление нулей многочленов с учетом кратности производится при помощи модифицированной схемы, изложенной в [12, 13]. Численный эксперимент вычисления нулей многочлена с учетом кратности по предложенной схеме выявляет ее устойчивость, а также повышенную точность для многочленов более высокой степени, чем в Mathcad.
Схема локализации и вычисления экстремальных значений и нулей решений систем обыкновенных дифференциальных уравнений. Пусть рассматривается задача Коши для уравнения
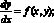y(x0) = y0. (5)
На промежутке [x0, xn] строится равномерная сетка, приближенное решение задачи (5) вычисляется по разностной схеме. Пусть для определенности выбран метод Эйлера:
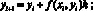xi = x0 + ih,
i = 1, 2, ..., n,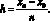 
(6)
Значения (6) принимаются за элементы сортируемого массива
c[i] = yi–1, i = 1, 2, ..., n. (7)
Элементы (7) сортируются. Присоединение условия локализации минимумов (максимумов) к программе сортировки элементов (7) влечет устойчивую локализацию и вычисление экстремумов приближенного решения задачи (5) [3, 15]. На промежутке с произвольно заданными границами [X00, Xnn] для исключения ложных экстремумов, как и выше, на концах текущих промежутков используется процедура сортировки с соответственным условием локализации экстремумов. Для случая системы дифференциальных уравнений схема применяется к каждому уравнению в отдельности. Детальное описание и другие примеры на случай системы приводятся в [7]. Для локализации нулей достаточно на вход сортировки подать абсолютные величины значений приближенного решения на равномерной сетке.
Локализация и вычисление собственных значений матриц. Собственные значения матрицы
вычисляются по описанной схеме как нули характеристического многочлена
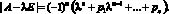
Его коэффициенты предварительно определяются по методу Леверье: решается система уравнений Ньютона:
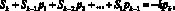
где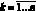 
, Sk = Sp(Ak) – след матрицы Ak. Многочлен 
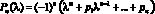(? = x + Iy) задан своими коэффициентами, для формирования соответственной многочлену функции f(x, y), которая подается на вход метода, используется биномиальное разложение [13] или значение многочлена умножается на комплексно-сопряженное значение. В результате
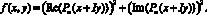
Если коэффициенты характеристического многочлена вычислены достаточно точно, то предложенный метод вычисления собственных значений матриц оказывается устойчивым ввиду фактически верного вычисления нулей многочленов с учетом кратности.
Приложение метода к анализу устойчивости. Метод анализа устойчивости линейной системы ОДУ с матрицей постоянных коэффициентов базируется на известных утверждениях: система устойчива тогда и только тогда, когда все характеристические нули матрицы правой части обладают неположительными вещественными частями, причем характеристические нули, имеющие нулевые вещественные части, допускают лишь простые элементарные делители. Система асимптотически устойчива тогда и только тогда, когда все характеристические нули матрицы правой части имеют отрицательные вещественные части. Алгоритм анализа устойчивости строится путем соединения этих утверждений с компьютерным методом идентификации нулей характеристического многочлена с учетом кратности на основе сортировки, инвариантным относительно области поиска нулей:
1. Вычисляются (локализуются с наперед заданной точностью) все нули характеристического многочлена без учета кратности.
2. Если среди них хоть один имеет положительную вещественную часть, то система неустойчива и анализ закончен. Иначе выполняется переход к п. 3.
3. Если число нулей с неположительной вещественной частью равно n, то они все различны и система устойчива. Анализ закончен. Иначе выполняется переход к п. 4.
4. Выполняется проверка кратности нулей с отрицательной вещественной частью. Если общее число нулей есть n, то характеристические нули с нулевой вещественной частью все различны, система устойчива, анализ закончен. Если общее число нулей меньше n, то среди нулей с нулевой вещественной частью имеются кратные, система неустойчива.
5. Конец алгоритма.
Вопрос об асимптотической устойчивости решается в один этап: если все нули имеют отрицательную вещественную часть, то система асимптотически устойчива, иначе система не является асимптотически устойчивой [1, 13].
Компьютерный анализ устойчивости можно дополнить методами из [3], распространяемыми на случай нелинейных систем.
Приложения к анализу экстремальных особенностей сигналов и изображений. Массив оцифрованных сигналов подается на вход сортировки в виде числовой последовательности. С некоторым радиусом локализации (радиус зависит от предметной области и природы сигналов) в этой последовательности идентифицируются все локальные экстремумы. Идентифицированные по значению и местоположению экстремумы интерпретируются как первичные экстремальные признаки объекта, который требуется выделить. Далее, выделяются все экстремумы в окрестности индекса каждого первичного экстремального признака. Полученное сочетание экстремумов интерпретируется в содержательном смысле исследуемой предметной области и выделяемого объекта. На этой основе удается частично автоматизировать диагностику электрокардиограмм [10], выделить объект по данным гидроакустической локации [9]. Наиболее существенные экстремумы (экстремальные признаки) можно найти автоматически, задав в программе итерации с возрастающим радиусом локализации до фиксированного числа повторений идентифицированных экстремумов. Так удается найти существенные признаки распознаваемого изображения [14], выделить тренд графического анализа, определить его тенденцию и точку разворота [11]. При этом целесообразно использовать преобразование последовательности первичных экстремумов как новой последовательности на вход метода, на этой основе удается выделить целочисленные идентификаторы для распознавания достаточно сложных изображений.
Заключение
Изложена схема программной идентификации нулей и экстремумов функций одной и более переменных в произвольной области. Дано приложение к разностным решениям систем ОДУ. Схема переносится на вычисление нулей многочленов с учетом их кратности, включая нули характеристического многочлена матрицы. Видоизменение этой же схемы применяется для компьютерного анализа устойчивости по Ляпунову системы ОДУ на основе метода Леверье и параллельного вычисления собственных значений матрицы постоянных коэффициентов системы линейных ОДУ. С дополнительным видоизменением схема распространяется на выделение объектов по экстремальным признакам оцифрованных сигналов и на распознавание растровых изображений.
Необходимо отметить, что изложенные схемы вычислений и распознавания исключают накопление погрешности в той своей части, где выполняется сортировка и сравнение индексов. На этой основе достигается высокая точность приближений. Поэтому для идентификации характера устойчивости линейных систем достаточно выбрать радиус локализации корней характеристического многочлена, сохраняющий только знак действительной части корня, что существенно ускоряет компьютерный анализ. В этом аспекте целесообразно принять во внимание параллелизм представленных схем.