ANALYSIS OF NORMAL STRESSES AT THE AREAS OF CONTACT OF PARTS OF THE MECHANISMS WITH A CLOSED SYSTEM OF ROLLING ELEMENTS, FOCUSED ON THE INNER RING AND ENTER THE AMENDMENT ON RADIUS OF THE SAME ELEMENT
Merko M.A. 1
Mesnyankin M.V. 1
Kayser Y.F. 1
Merko I.S. 1
Lysyannikov A.V. 1
Kolotov A.V. 1
Mityaev A.E. 1
Lysyannikova N.N. 1
Rabetskaya O.I. 1
Merko A.M. 1
1 Siberian Federal University
The analysis of the problem. The solution of the problem of determining the normal stress at the sites of contact units mechanisms with the closed system of the rolling elements with diameters of different sizes in the leading inner ring for any kind of symmetrical structural scheme.The formulas for calculating the normal stresses in the contact zones and reduced radius of curvature of the contacting surfaces of links of mechanisms of this type.Set a range of possible values when entering amendments in the calculation of the nominal values of geometrical parameters on the radius of the raceway of the inner ring. The results allow shaping of the drive of technological equipment on the basis of mechanisms with a closed system of rolling elements having the required load capacity. Developed software complex «Eccentric» registered in the Registry of computer programs of the Federal service for intellectual property of Russia (ROSPATENT), allowing to improve the effectiveness as the research, engineering developments.
rolling body closed system
mechanism with rolling body closed system
rolling body
cage
raceway
sliding speed
the area of contact
contact platform
normal voltage
1. Merko M.A. Kinematicheskie i geometricheskie harakteristiki jekscentrikovogo mehanizma kachenija: avtoref. dis. ... kand. tehn. nauk: 05.02.02. Krasnojarsk, 2002. 26 р.
2. Merko M.A., Mesnjankin M.V., Kajzer Ju.F., Kolotov A.V., Mitjaev A.E., Lysjannikov A.V., Kuznecov A.V. Peredatochnye otnoshenija planetarnyh mehanizmov s ZSTK s diametrami ravnoj velichiny pri vedushhem vnutrennem kolce i vvode popravki po radiusu dorozhki kachenija jetogo zhe zvena // Sovremennye problemy nauki i obrazovanija. 2014. no. 1; URL: www.science-education.ru/115-12219.
3. Merko M.A., Mesnjankin M.V., Kolotov A.V.,
Kajzer Ju.F., Lysjannikov A.V. Korrektirovka rascheta geometricheskih parametrov mehanizmov s ZSTK po radiusu dorozhki kachenija vnutrennego kolca // Sovremennye problemy nauki i obrazovanija. 2013. no. 6. URL: www.science-education.ru/113-11778.
4. Merko M.A., Mesnjankin M.V., Merko I.S., Mi-
tjaev A.E., Kolotov A.V., Kajzer Ju.F., Lysjannikov A.V., Lysjannikov N.N. Raspredelenie staticheskih sil po tochkam kontakta zvenev mehanizmov s zamknutoj sistemoj tel kachenija v zone minimalnyh diametrov // Sovremennye problemy nauki i obrazovanija. 2014. no. 6; URL: www.science-education.ru/120-15346.
5. Merko M.A., Mesnjankin M.V., Mitjaev A.E., Kolotov A.V. Raspredelenie staticheskih sil po tochkam kontakta zvenev mehanizmov s zamknutoj sistemoj tel kachenija v zone maksimalnyh diametrov // Sovremennye problemy nauki i obrazovanija. 2014. no. 3; URL: www.science-education.ru/117-13473
6. Mesnjankin A. V., Merko M. A., Kolotov A. V., Mitjaev A.E. Opredelenie granic oblastej sushhestvovanija mehanizmov-prototipov JeMK pri vvode popravki v raschet po dorozhke kachenija vnutrennego kolca // Vestnik KrasGAU. Krasnojarsk, 2012. no. 12. рр. 138–141.
7. Mesnjankin M.V., Merko M.A., Kolotov A.V., Mitjaev A.E. Rezultaty reshenija zadachi o polozhenijah zvenev JeMK pri vedushhem vnutrennem kolce // Vestnik Tadzhikskogo tehnicheskogo universiteta. 2013. no. 1. рр. 35–41.
8. Mesnjankin M.V., Merko M.A., Kolotov A.V., Mitjaev A.E. Skorosti skolzhenija tochek kontakta zvenev meanizmov s ZSTK s diametrami raznoj velichiny pri vedushhem naruzhnom kolce i vvode popravki po radiusu dorozhki kachenija jetogo zhe zvena // Sovremennye problemy nauki i obrazovanija. 2014. no. 2. URL: www.science-education.ru/116-12979.
9. Mesnjankin M.V., Merko M.A., Kolotov A.V., Mitjaev A.E. Uslovija simmetrii mehanizmov s zamknutoj sistemoj tel kachenija // Vestnik Tadzhikskogo tehnicheskogo universiteta. 2013. no. 3. рр. 29–34.
Обеспечение радиальной грузоподъемности при снижении габаритных размеров и массы механизмов приводов технологического оборудования является приоритетным направлением модернизации предприятий России в условиях импортозамещения. Грузоподъемность механизмов качения оценивается напряженно-деформированным состоянием контактирующих звеньев, содержащихся в структуре механизма. Данное состояние является следствием возникновения роста концентрации нормальных напряжений, вызванных упругими деформациями, приводящими к образованию площадок контакта между звеньями механизма, что является следствием действия радиальной нагрузки на его ведущее звено. Напряженно-деформированное состояние вызывает усталостное старение материалов, из которых изготовлены звенья механизма, и создает предпосылки для образования областей повышенных напряжений на рабочих поверхностях контактирующих звеньев. Данные явления значительно снижают грузоподъемность механизма и отрицательно влияют на большинство его показателей качества. Исключение указанных отрицательных явлений обеспечивается использованием многопоточных механизмов, обладающих новой структурой при минимально возможном числе подвижных звеньев. Эти обстоятельства выводят на новый этап развития науки и техники механизмы с замкнутой системой тел качения (ЗСТК). Структура механизмов данного вида образована совокупностью двух колец с дорожками качения, сепаратором (водило) и замкнутой системой тел качения с диаметрами как разной (эксцентриковые) [1–5, 7, 8], так и равной величины (соосные) [6, 9]. Тела качения могут обладать гладкими рабочими поверхностями (фрикционные) или поверхностями с выступами (зубчатые). Для механизмов с ЗСТК с диаметрами разной величины характерно наличие нескольких видов симметричных структурных схем (рис. 1), каждая из которых может реализоваться как с зазором между телами качения, так и при отсутствии в структуре данного параметра.
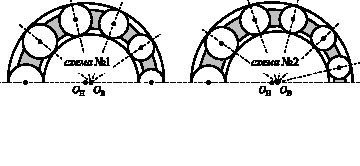
а б
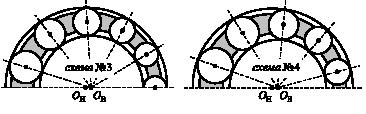
в г
Рис. 1 Виды симметричных структурных схем механизмов с ЗСТК
Коллектив авторов проводит исследования геометрических, кинематических и силовых параметров приводов технологического оборудования, разработанных на базе механизмов с ЗСТК. В ходе исследований авторами установлено: задача определения номинальных величин геометрических параметров механизмов с ЗСТК должна решаться при начальных условиях, что исходные параметры являются постоянными величинами больше нуля [1, 3, 6]. Дальнейшие исследования показали, что для решения задачи по определению номинальных величин геометрических параметров при данных условиях необходим ввод поправки в расчет, считая один из исходных параметров величиной переменной. Вариация значениями радиуса тел качения и зазора между ними не позволяет достичь требуемого результата. В этом случае получаем, что решение задачи имеет два возможных направления ввода поправки: либо по радиусу дорожки качения наружного кольца, либо по радиусу дорожки качения внутреннего кольца.
Настоящее исследование проводится с целью разработки алгоритма определения нормальных напряжений на площадках контакта звеньев механизмов с ЗСТК с диаметрами разной величины при ведущем внутреннем кольце для любого вида симметричной структурной схемы и вводе поправки в расчет номинальных величин геометрических параметров по радиусу дорожки качения этого же звена. Полученные результаты позволят формировать приводы технологического оборудования на базе механизмов с ЗСТК, обладающих требуемой радиальной грузоподъемностью.
Методы исследования, применяемые в настоящей работе, основаны на принципах силового анализа и методах определения грузоподъемности механизмов при использовании положений геометрии.
Рассмотрим определение нормальных напряжений на площадках контакта звеньев на примере механизма с ЗСТК с диаметрами разной величины при ведущем внутреннем кольце для любого вида симметричной структурной схемы и вводе поправки в расчет номинальных величин геометрических параметров по радиусу дорожки качения этого же звена. Внешняя радиальная нагрузка приложена к ведущему звену механизма. В этом случае для обеспечения работоспособности механизма данного вида необходимо, чтобы нормальные напряжения не превышали допускаемой величины, что возможно при выполнении условия прочности, которое имеет общеизвестный вид
?max ? [?Н], (1)
где ?max и [?Н] - максимальное и допускаемое нормальные напряжения.
Для механизма с ЗСТК рассматриваемого вида имеет место контакт тел качения, выполненных в виде роликов, с дорожками качения обоих колец, имеющих цилиндрическую форму, следовательно, условие прочности (1) может быть представлено как
?i(В, Н) ? [?Н], (2)
где ?i(В, Н) - нормальные напряжения на площадках контакта i-го тела качения с дорожками качения внутреннего и наружного колец.
Нормальные напряжения на площадках контакта i-го тела качения с дорожками качения внутреннего и наружного колец найдем по формуле
здесь Fi(В, Н) - сила, действующая в зоне контакта i-го тела качения с дорожкой качения внутреннего или наружного колец; Ei, Eд(В, Н), ?i и ?д(В, Н) - модули упругости и коэффициенты Пуассона материалов i-го тела качения и внутреннего или наружного колец; lpi - длина рабочей части i-го тела качения; ?i(В, Н) - приведенный радиус кривизны контактирующих поверхностей i-го тела качения с дорожкой качения внутреннего или наружного колец.
Приведенный радиус кривизны контактирующих поверхностей i-го тела качения с дорожкой качения определим по выражениям:
– для внутреннего кольца
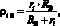 (4)
(4)
– для наружного кольца
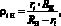 (5)
(5)
где ri, RВ, RН - радиусы i-го тела качения и дорожек качения внутреннего и наружного колец соответственно.
Анализ формулы (3) показывает, что большинство ее составляющих учитывают свойства материалов контактирующих звеньев механизма с ЗСТК. Это означает, что для удобства дальнейшего анализа формулу (3) приведем к виду
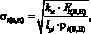 (6)
(6)
здесь kм - коэффициент, учитывающий свойства материалов звеньев механизма с ЗСТК, определяемый по равенству
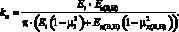 (7)
(7)
Анализируя формулу (6), видим, что нормальные напряжения на площадках контакта i-го тела качения с дорожками качения обоих колец зависят от нормальной силы, длины рабочей части тел качения и приведённого радиуса кривизны. В работах [4, 5] авторами предложен алгоритм определения статических сил, возникающих в точках контакта звеньев механизма с ЗСТК, где показано, что на тела качения, расположенные в зоне нагружения от внешней суммарной радиальной нагрузки, действуют силы не одинаковой величины.
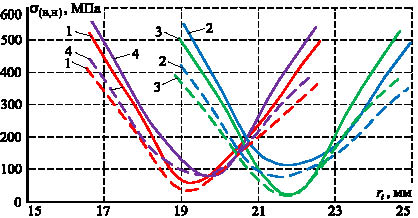
Используя формулы (4)–(7) выполняем расчет величин нормальных напряжений на площадках контакта тела качения с дорожкой качения обоих колец для всех видов симметричных структурных схем (рис. 1) и вводе поправки в расчет геометрических параметров по радиусу дорожки качения внутреннего кольца. При вычислениях считаем, что внешняя суммарная радиальная нагрузка действует на ведущее внутреннее кольцо и равна Q = 10 кН. Коэффициенты Пуассона и модули упругости материалов звеньев соответственно равны ?i = ?д(В, Н) = 0,3; Ei = Eд(В, Н) = 2,1?105 МПа. Механизмы с ЗСТК обладают геометрическими параметрами: радиусы дорожек качения наружного (RН = 100 мм) и внутреннего (RВ = 50 мм) колец, эксцентриситет е = 6 мм, зазор между телами качения с = 6 мм. Длина рабочей части тел качения lpi = 20 мм. С целью повышения эффективности процесса вычислений авторами разработано программное обеспечение в виде программного комплекса «Эксцентрик», зарегистрированного в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности Российской Федерации (РОСПАТЕНТ № 2012614197). По результатам вычислений выполняем синтез диаграммы нормальных напряжений для всех видов симметричных структурных схем механизмов с ЗСТК с диаметрами разной величины (рис. 1) при ведущем внутреннем кольце (рис. 2).
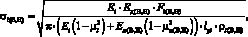 (3)
(3)
Анализ диаграммы (рис. 2) показывает, что все полученные кривые нормальных напряжений имеют параболический вид. При этом для любого вида симметричной структурной схемы механизма с ЗСТК (рис. 1) нормальные напряжения принимают большие значения на площадках контакта тел качения с дорожкой качения внутреннего кольца. Это является следствием меньшей величины приведенного радиуса кривизны контактирующих поверхностей. Дальнейший анализ диаграммы показывает, что также для любого вида симметричной структурной схемы минимальные значения нормальных напряжений имеют место на площадках контакта тел качения, не расположенных на линии действия вектора внешней суммарной радиальной нагрузки. Максимальные величины для рассматриваемых напряжений наблюдаются на площадках контакта дорожек качения колец с телами качения минимального и максимального диаметров. При принятых условиях расчета максимальные контактные напряжения имеют для симметричных структурных схем механизмов с ЗСТК, представленных на рис. 1, б, г. В то же время для любого вида симметричной структурной схемы механизма рассматриваемого вида максимальные напряжения имеют место всегда на площадке контакта дорожек качения обоих колец с минимальным телом качения, находящегося на линии действия вектора внешней суммарной радиальной нагрузки. Данное явление означает, что радиальную грузоподъемность механизма с ЗСТК с диаметрами разной величины необходимо определять по нормальным напряжениям, которые имеют место на площадке контакта тела качения с минимальным диаметром при его контакте с внутренним кольцом.
Получены формулы для расчета нормальных напряжений на площадках контакта звеньев механизмов с ЗСТК с диаметрами разной величины при ведущем внутреннем кольце для любого вида симметричной структурной схемы. Определены диапазоны возможных значений нормальных напряжений рассматриваемого вида при вводе поправки в расчет номинальных величин геометрических параметров по радиусу дорожки качения внутреннего кольца, удовлетворяющих условию прочности (2). Установлено, что радиальная грузоподъемность механизма с ЗСТК с диаметрами разной величины необходимо определять по нормальным напряжениям, которые имеют место на площадке контакта тела качения с минимальным радиусом. Полученные результаты позволят формировать приводы технологического оборудования на базе механизмов с ЗСТК, обладающих требуемой радиальной грузоподъемностью.






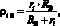 (4)
(4)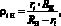 (5)
(5)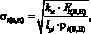 (6)
(6)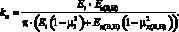 (7)
(7)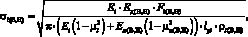 (3)
(3)
 внутреннего и
внутреннего и  наружного колец
наружного колец