В последнее время значительная часть исследований в робототехнике посвящена вопросам применения мобильных роботов: показывается перспективность их использования в задачах автоматизации технологических процессов, мониторинга, исследования окружающей местности и многих других приложениях. В этой связи особый интерес представляет взаимодействие агентов в группах мобильных роботов, так как использование мобильных роботов в составе группы позволяет увеличить надежность в целом, сократить время выполнения поставленной задачи и гарантировать ее выполнение даже при выходе из строя отдельных роботов. Поэтому не теряет актуальности одна из фундаментальных проблем робототехники: планирование оптимальных маршрутов движения мобильных роботов, одновременно функционирующих в пределах единого рабочего пространства. Сложность решения проблемы определяется недетерминированностью окружающей обстановки; повышенными требованиями к бортовой системе управления: необходимо принятие решений в реальном масштабе времени при наличии дефицита ресурсов. Поэтому известные системы планирования группами роботов часто строятся с использованием различных методов искусственного интеллекта [5–7].
Как показывают результаты сравнительного анализа эффективности интеллектуальных алгоритмов, используемых для решения рассматриваемой задачи, результаты их работы в большей мере зависят от требуемого уровня детализации маршрута, количества роботов в группе, наличия и объема сенсорной информации [1]. Также большое влияние на результат работы имеют некоторые специфические особенности применяемых методов: генетические алгоритмы (ГА) позволяют избежать появления локальных экстремумов; нейросети могут быть реализованы с использованием нейроускорителей, а также обладают способностью быстрой адаптации с организацией пере- или дообучения в реальном времени, нечеткие алгоритмы (НА) нетребовательны к аппаратным ресурсам при достаточно высокой скорости обработки.
Поэтому при планировании траекторий движения в группах мобильных роботов представляется актуальным применение гибридных интеллектуальных систем, построенных с одновременным использованием нескольких методов: одновременная работа компенсирует недостатки одного преимуществами другого, тем самым позволяя находить решения, недоступные отдельным интеллектуальным методам.
Гибридная архитектура системы планирования
Гибридная система будет эффективна в условиях, когда возможности систем технического зрения (СТЗ) не позволяют в полной мере обеспечить расчет безопасных траекторий, что связано с малыми габаритами объектов в рабочем пространстве или в больших по площади рабочих зонах [3]. Когда разрешающей способности СТЗ недостаточно для синтеза безопасных траекторий движения, выполняемое при этом планирование движений может быть отнесено к грубому планированию. Благодаря низкому уровню детализации алгоритмы грубого планирования отличаются быстросчетностью и позволяют легко решать оптимизационную задачу в соответствии с одновременно задаваемыми критериями: минимальной длиной маршрута, минимизацией времени перемещения и т.д. Однако это не снимает необходимости и в точном планировании траекторий: для исключения столкновений в рабочей зоне, обеспечения безопасных расстояний относительно препятствий и других роботов. Недостаточная разрешающая способность СТЗ в этом случае компенсируется бортовыми сенсорными системами роботов (ближняя локация). При одновременном использовании этих методов система планирования будет иметь гибридную архитектуру (рис. 1).
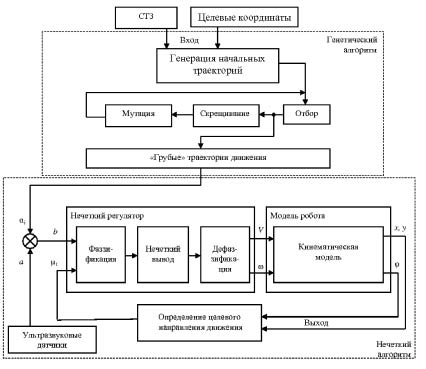
Рис. 1. Архитектура гибридной интеллектуальной системы планирования траекторий мобильных роботов
Подсистема грубого планирования
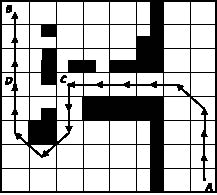
Гибридная архитектура системы позволяет формировать оптимальную траекторию в двух приближениях: грубом и точном. На этапе грубого планирования формируется модель внешней среды для поиска приближенной траектории с использованием ГА. В качестве базового метода поиска используется метод планирования для группы мобильных роботов [4], в котором:
? изменены используемые критерии качества;
? изменен набор генетических операторов;
? увеличен шаг дискретизации.
Это позволяет сократить наиболее затратные в вычислительном плане математические операции и увеличить общее быстродействие алгоритма. Получаемое при этом некоторое снижение качества траектории компенсируется подсистемой точного планирования.
Как и в базовом методе, для описания модели внешней среды используются матрицы размерностью Sx?Sy, элементы которых принимают логические значения «0» или «1» в зависимости от того, свободна или занята препятствием соответствующая ячейка сетки. Количество матриц N выбирается в зависимости от шага квантования по времени и характеризует период, в течение которого движение препятствий (других роботов) в рабочей области задано, определяя максимальную глубину планирования по времени. В качестве индивидуумов рассматриваются маршруты движения по ячейкам сеток, а хромосома представляет собой последовательность N узлов, образующих траекторию движения. Первый узел является стартовой точкой маршрута, а последний узел – конечной. В качестве функции пригодности служит следующий функционал:
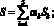
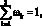
где ?k = const ? [0, 1] – весовые коэффициенты; Sk – нормированные значения функций соответствия, вычисляемых для проверки степени близости потенциального решения по заданному k-му критерию к оптимальному маршруту.
Функция соответствия S1 характеризует критерий оптимальности по длине траектории:
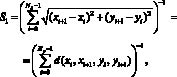
где xi и yi – координаты текущей точки, xi + 1 и yi + 1 – координаты следующей точки, d(xi, xi + 1, yi, yi + 1) = 1 при перемещении в соседнюю ячейку по горизонтали и вертикали, и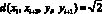 
– по диагонали.
Функция соответствия S2 характеризует критерий оптимальности по времени, затраченному на движение по маршруту:
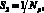
где Np – длина хромосомы.
Использование двух функций S1 и S2 позволяет выбирать из популяции оптимальный маршрут независимо от скорости движения робота вдоль пути.
После процедуры отбора из популяции наиболее приспособленных особей на их базе осуществляется процесс генерации новых поколений. Новое поколение хромосом генерируется посредством двух классических операций: скрещивания и мутации, которые подобны традиционным схемам «размножения», используемым в классических ГА. Полученное на этом этапе решение является приближенным, окончательный вид траектории формируется уже подсистемой точного планирования.
Подсистема точного планирования
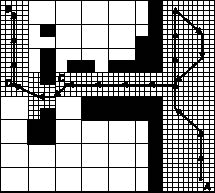
При перемещении вдоль найденной грубой траектории движения сенсорные системы ближней локации дополняют модель рабочего пространства, которая была построена с помощью СТЗ. Больший уровень детализации окружающей обстановки, обеспечиваемый бортовыми сенсорными системами, позволяет уменьшить шаг дискретизации модели рабочего пространства и внести коррекцию в отдельные участки спланированной грубой траектории движения.
Подсистема точного планирования основана на НА [2]. В качестве входных сигналов нечёткого регулятора используется следующая информация: A – свободные области рабочей зоны; b – угловое отклонение от цели.
Свободные области рабочей зоны A – это матрица, формируемая на основе информации, поступающей от датчиков, расположенных в каждом из восьми возможных направлений движения (рис. 2, а). Угловое отклонение от цели b – входная переменная, определяющая отклонение курса движения мобильного робота от целевого направления (рис. 2, б).
Выходными сигналами нечеткого регулятора являются линейная скорость мобильного робота V и направление движения мобильного робота ?. Направление движения ? – это выходная переменная, определяющая необходимое угловое смещение робота, при этом значение этого параметра необязательно должно совпадать со значением входной переменной b. Входным и выходным сигналам соответствуют логико-лингвистические переменные, значения которых определяются термами-множествами. На их основе строится база знаний нечеткой системы, состоящая из продукционных правил и отражающая зависимость между входными и выходными термами-множествами. Всего в базе правил определено 72 правила – по девять вложенных правил для каждого из восьми значений углового отклонения робота от цели.
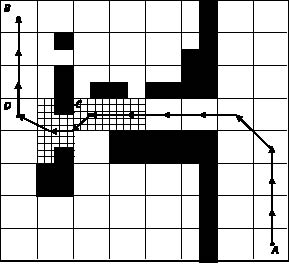
В базе правил поиск выполняется по узловым точкам грубой траектории движения. Если расстояние по найденному маршруту между узловыми точками меньше, чем расстояние, которое проходит робот по начальной грубой траектории, то его дальнейшее движение осуществляется по этому маршруту, поэтому на отдельных участках маршрута робот может двигаться по грубой траектории, а на других – по точной траектории.
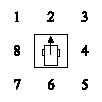
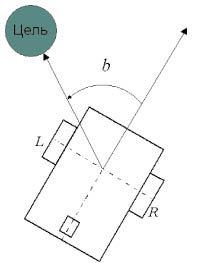
а б
Рис. 2. а – кодировка элементов матрицы; б – угловое отклонение от цели
