Ферромагнитные материалы с памятью формы (ФМПФ) могут контролируемым образом преобразовывать один вид энергии в другой [1]. Это дает возможность использовать эти материалы для выполнения исполнительных и измерительных функций, повысить точность преобразования, упростить конструкцию устройств. В последнее время ведутся исследования и разработки исполнительных и измерительных систем с активными элементами (АЭ) из ФМПФ [6–8]. На использование таких систем, в том числе короткоходных линейных электроприводов, в промышленных системах управления технологическими процессами накладываются повышенные требования к точности определения параметров и надежности. Для проведения функциональной диагностики электропривода, построенного на основе ФМПФ [7], предложены математическая модель привода [2, 3] и методика метрологической оценки результатов испытаний [4], позволяющие прогнозировать параметры системы управления приводом. Однако определение эксплуатационных характеристик АЭ затруднено. Физические свойства АЭ имеют нелинейный характер. Как правило, они являются элементами сложной системы и проявляют свои свойства в полной мере лишь в собранной системе. Одним из путей решения указанной проблемы является синтез эмпирических законов управления электроприводами на основе ФМПФ по результатам натурно-модельных испытаний.
Принцип работы электропривода [7] основан на изменении линейного размера (деформации) АЭ из ФМПФ под воздействием напряженности магнитного поля, вектор которой направлен перпендикулярно плоскости изменения размера. Для обеспечения больших деформаций АЭ создается импульсное магнитное поле с напряженностью до 350 кА/м. Используется магнитная система электропривода, учитывающая эти особенности [5].
Сформулируем следующую задачу управления. Необходимо выполнить деформацию АЭ электропривода на заданную величину при допустимой ошибке управления ? ? 0,5 мкм. Задача сводится к обеспечению приращения длины АЭ из ФМПФ на заданную величину от результирующего воздействия – импульса магнитного поля (или серии импульсов) с определенной амплитудой и длительностью.
Следует учитывать, что при эксплуатации электроприводов предъявляют дополнительное условие к управлению – исключение возможности перерегулирования. Конкретизируем это условие применительно к электроприводам на основе ФМПФ: фактическая длина Lкф АЭ после управляющего воздействия должна быть строго меньше заданного значения конечной длины Lкз на величину допустимой ошибки управления DLоу (ошибки позиционирования) (рис. 1).
Алгоритм управления электроприводом на основе ФМПФ включает выполнение следующих этапов: генерацию управляющего импульса для перемагничивания АЭ; измерение фактической длины Lкф АЭ; вычисление ошибки управления DLоу; анализ полученного результата; определение параметров корректирующего управляющего импульса. Блок-схема алгоритма показана на рис. 2. Его реализация предполагает предварительную разработку эмпирических законов управления. Они представляют собой экспериментально полученные зависимости перемещений АЭ от различных управляющих воздействий при варьируемых начальных условиях, обусловленных наличием начальной деформации АЭ. Различные начальные деформации АЭ воспроизводят результат действия управляющих импульсов на предыдущих итерациях алгоритма управления.
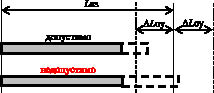
Рис. 1. Иллюстрация дополнительного условия к управлению электроприводом
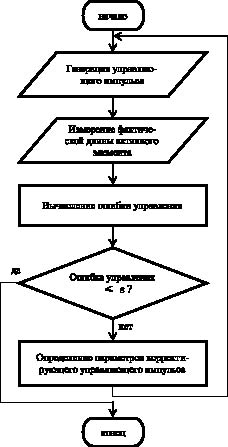
Рис. 2. Блок-схема алгоритма управления электроприводом
Задача разработки эмпирического закона управления формулируется следующим образом. Заданному значению деформации АЭ (заданному значению его конечной длины Lкз) поставить в соответствие значение амплитуды первичного управляющего импульса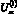 
, а также таблицу значений амплитуды вторичного управляющего импульса 
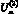как функции от фактической длины активного элемента 
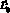после первичного воздействия:
(*)
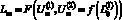Выражение (*), по сути, представляет собой аналитическую запись эмпирического закона управления электроприводом с одним корректирующим воздействием.
В общем случае необходимо несколько корректирующих воздействий. При этом аналитическая запись эмпирического закона управления с несколькими корректирующими воздействиями примет вид
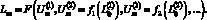
Рассмотрим методику синтеза эмпирических законов управления электроприводом на основе ФМПФ, состоящую из следующих этапов.
Первый этап включает теоретическое определение амплитуды первичного управляющего импульса. При этом на основе математической модели определяется необходимая амплитуда управляющего импульса для достижения заданной конечной длины Lкз АЭ.
На втором этапе экспериментально определяется разброс результатов первичного управляющего воздействия sу. Для этого производится серия экспериментов и определяется разброс значений фактической деформации активного элемента sу (рис. 3).
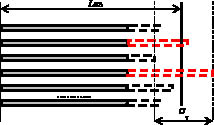
Рис. 3. Разброс значений фактической деформации АЭ
Третий этап предназначен для корректировки амплитуды первичного управляющего импульса с целью исключения ситуаций перерегулирования. При этом амплитуда первичного управляющего импульса с учетом значения sу корректируется (уменьшается) таким образом, чтобы в серии экспериментов максимальная деформация АЭ не привела бы к превышению заданного значения конечной длины активного элемента Lкз.
На четвертом этапе выполняется проверка условия завершения процесса разработки эмпирического закона управления. Проверяется, обеспечивается ли заданная точность управления в результате предыдущих управляющих воздействий и, соответственно, завершено ли формирование закона управления (рис. 4).
На последующих итерациях повторяются действия предыдущих этапов, но уже проводится не одна, а несколько серий экспериментов с условием определенного значения начальной деформации активного элемента для каждой серии. Эти величины начальных деформаций определяются множеством значений фактической конечной длины активного элемента, выявленных в серии экспериментов на первой итерации (после подачи первичного управляющего импульса). При этом все множество упомянутых значений может быть «прорежено» с точностью до допустимой ошибки управления DLоу доп.
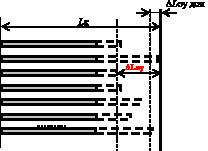
Рис. 4. Условие завершения процесса разработки закона управления электроприводом
Таким образом, на каждой последующей итерации подбираются параметры корректирующих управляющих импульсов, исходя из фактического приращения АЭ на предыдущей итерации.
Вычислительный эксперимент
С целью исследования методики синтеза эмпирических законов управления проводился вычислительный эксперимент. Для его реализации разработан программный модуль в среде графического программирования LabVIEW.
Для ввода данных в программу используется кластерный элемент управления. Задаются значения следующих параметров: количество значений аргумента (амплитуда управляющего сигнала), по которым будут рассчитываться функциональные зависимости; минимальная и максимальная амплитуды управляющего сигнала; теоретически минимальные и максимальные возможные приращения длины АЭ; параметр экспоненты в функциональной зависимости приращения АЭ от амплитуды управляющего сигнала; заданная величина приращения длины АЭ; количество экспериментов, проведенных при одном определенном значении амплитуды управляющего сигнала, определенной на основе теоретической модели для достижения заданной величины приращения длины АЭ; максимально допустимая реальная величина приращения длины АЭ.
В программе используется полученная на основе математического моделирования теоретическая функция величины приращения длины АЭ:
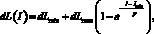
где dLmin – минимально возможное приращение длины активного элемента после управляющего воздействия импульсом с минимальной пороговой амплитудой Imin; dLmax – максимально возможное приращение длины активного элемента; I – амплитуда управляющего импульса; p – параметр показателя экспоненты.
На рис. 6 показаны графики теоретической и действительной зависимости величины приращения длины АЭ от амплитуды управляющего сигнала. На рисунке: 1 – теоретическая зависимость величины приращения длины АЭ от амплитуды управляющего сигнала; 2 – действительная зависимость величины приращения длины АЭ от амплитуды управляющего сигнала; 3 и 4 – диапазон изменения приращения длины АЭ в зависимости от амплитуды управляющего сигнала.
Точка 5 (рис. 5) соответствует заданному значению приращения длины АЭ и, соответственно, определенному исходя из теоретических представлений, необходимой амплитуде управляющего сигнала. Точка 6 соответствует действительному значению приращения длины АЭ после управляющего воздействия импульсом с амплитудой, определенной исходя из теоретических представлений.
Действительная зависимость величины приращения длины АЭ от амплитуды управляющего сигнала и диапазон ее варьирования, отображаемые на графике на рис. 6, формируются в результате обработки данных большого комплекса экспериментов.
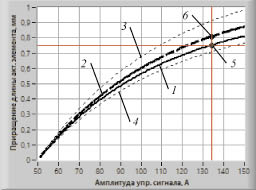
Рис. 5. Графики теоретической и действительной зависимости величины приращения длины АЭ от амплитуды управляющего сигнала
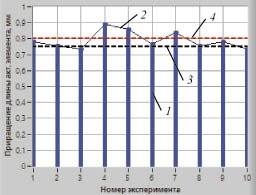
Рис. 6. График множества экспериментально полученных значений приращений длины АЭ после управляющего воздействия с определенной амплитудой
График на рис. 6 содержит следующие элементы: 1 – множество экспериментально полученных значений приращений длины АЭ после управляющего воздействия; 2 – соединительная линия для отображаемых экспериментальных значений приращений длины активного элемента; 3 – заданное значение приращения длины активного элемента после управляющего воздействия; 4 – максимально допустимое приращение длины активного элемента после управляющего воздействия.
Экспериментальный график на рис. 6 соответствует теоретическому, приведенному на рис. 3. Таким образом, разработанный программный модуль является инструментом, обеспечивающим выполнение первого, второго и третьего этапов синтеза эмпирических законов управления электроприводом на основе ФМПФ, описанных выше. Используя графический элемент, показанный на рис. 6, в соответствии с третьим этапом, необходимо скорректировать амплитуду управляющего сигнала таким образом, чтобы избежать ситуации превышения максимально допустимого приращения АЭ.
Анализ полученных результатов показывает, что применение методики синтеза эмпирических законов управления позволяет обеспечить деформацию АЭ электропривода на заданную величину с ошибкой управления ? ? 0,5 мкм.
Выводы
1. Описанный в статье подход, основанный на натурно-модельном принципе управления, когда теоретически полученные математические модели управляемых объектов настраиваются по результатам экспериментальных исследований, позволяет повысить точность управления короткоходными линейными электроприводами на основе ФМПФ.
2. Синтез эмпирических законов управления электроприводами на основе ФМПФ связан с разработкой методик накопления, упорядочивания и систематизации экспериментальных данных, а также с разработкой инструментария, реализующего эти методики в виде компьютерной программы обработки данных. На выходе этой программы будут синтезироваться законы управления электроприводами на основе ФМПФ.
Результаты работы получены при поддержке гранта РФФИ № 14-08-01288 «Разработка теории натурно-модельных испытаний измерительных и исполнительных систем, построенных на основе ферромагнитных материалов с эффектом памяти формы».