MATHEMATICAL MODEL OF PROCESS OF MEMBRANE CONCENTRATION OF STARCH MILK BASED ON TRANSFER FUNCTIONS
Khachatryan L.R. 1
1 Federal State-owned Budgetary Educational Institution of Higher Education «Kemerovo Institute of Food Science and Technology (university)», Kemerovo
This article is dedicated to the development of the mathematical model on the basis of transfer functions that describes the dynamics of process of membrane concentration of starch milk in the ultrafiltration apparatus. The construction and principle of operation of the ultrafiltration apparatus with hydrodynamic elements are described. The main inputs and outputs of object of modeling are revealed. The block diagram of process of membrane concentration is made. The type of inputs is chosen. The type of transfer functions of channels of influence of initial concentration, working pressure and temperature of product upon productivity is determined. The ranges of inputs are experimentally determined during the process of membrane concentration of starch milk. The parameters of transfer functions are found by means of processing of experimental dependences. The mathematical model of process of membrane concentration is realized by software. The results of estimation of adequacy of model to experimental data are given.
mathematical modeling
transfer friction
membrane concentration
ultrafiltration
starch milk
1. Antonov, A.V. Sistemnyj analiz [System analysis] / A.V. Antonov. Moscow, Vysshaja shkola, 2004. 454 p.
2. Volkova, V.N. Osnovy teorii sistem i sistemnogo analiza [Bases of the theory of systems and system analysis] / V.N. Volkova, A.A. Denisov. St. Petersburg, SPbGPU, 1999. 512 p.
3. Erofeev, A.A. Teorija avtomaticheskogo upravlenija [Theory of automatic control] / A.A. Erofeev. St. Petersburg, Politehnika, 2003. 302 p.
4. Lure, B.Ja. Klassicheskie metody avtomaticheskogo upravlenija [Classical methods of automatic control] / B.Ja. Lure, P.Dzh. Jenrajt. St. Petersburg, BHV-Peterburg, 2004. 640 p.
5. Hachatrjan L.R., Kotljarov R.V. Membrannyj apparat [Membrane apparatus]. Patent RF no. 152744, 2015.
6. Hachatrjan L.R. Issledovanie tekhnologicheskih rezhimov raboty membrannogo apparata pri koncentrirovanii krahmalnogo moloka [Research on technological modes of operating of membrane apparatus for starch milk concentration] / L.R. Hachatrjan, R.V. Kotlyarov, B.A. Lobasenko //Food Processing: Techniques and Technology. Kemerovo, 2015. no. 2(37). рр. 61–66.
Математическое моделирование является неотъемлемой частью современного научного исследования. Математическая модель представляет собой эффективный инструмент познания реального объекта и позволяет определить его характеристики, получить оценку показателей эффективности качества, осуществить поиск оптимальной структуры и параметров объекта.
Универсальным методом математического моделирования является использование передаточных функций, которые позволяют описывать динамические свойства системы практически любой структуры и сложности. Передаточная функция представляет собой динамический оператор, характеризующий прохождение сигналов через систему. Совокупность передаточных функций образует математическую модель системы, позволяющую оценивать и прогнозировать процессы, происходящие в ней.
Целью данной статьи является описание этапов моделирования процесса мембранного концентрирования крахмального молока в ультрафильтрационном аппарате с гидродинамическими элементами: анализ объекта моделирования, структурная и параметрическая идентификация математической модели, проверка адекватности модели.
Материалы и методы исследования
Объектом моделирования является процесс мембранного концентрирования крахмального молока в ультрафильтрационном аппарате с гидродинамическими элементами (рис. 1) [5]. Аппарат содержит корпус 1, выполненный в виде цилиндра. С одной стороны корпуса располагается патрубок 2 для подачи исходного потока, с другой – патрубок 3 для отвода конечного продукта в виде концентрата, а также патрубок 4 для отвода фильтрата. Внутри корпуса располагается коаксиально полупроницаемая мембрана 5. В мембране располагается вставка, состоящая из несущего стержня 6, гидродинамических элементов 7 и фиксирующих колец 8.
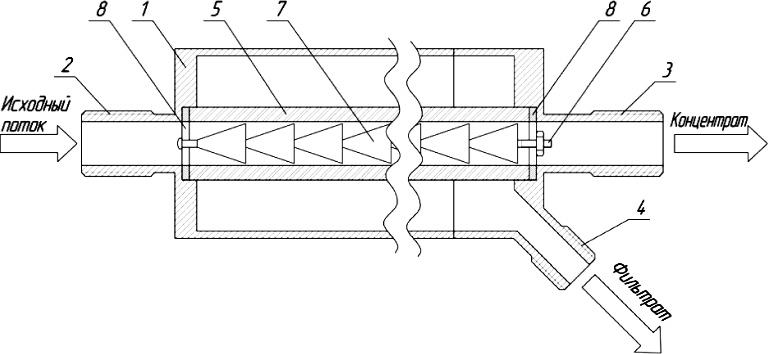
Рис. 1. Ультрафильтрационный аппарат: 1 – корпус; 2 – патрубок для подачи исходного потока; 3 – патрубок для отвода концентрата; 4 – патрубок для отвода фильтрата; 5 – фильтрующий элемент (мембрана); 6 – несущий стержень вставки; 7 – гидродинамические элементы вставки; 8 – фиксирующие кольца
Исходный раствор под давлением подается через патрубок 2 во внутренний канал мембраны 5. В процессе мембранного концентрирования на внутренней поверхности фильтрующего элемента формируется слой осадка, который снижает производительность аппарата. По ходу движения потока внутри мембраны, за счет уменьшающегося зазора между гидродинамичеким элементом 7 и внутренней стенкой мембраны 5, происходит увеличение его скорости. Благодаря этому осуществляется очистка поверхности фильтрующего элемента от образующихся отложений. Прошедший через мембрану фильтрат отводится через патрубок 4. Оставшаяся часть исходного раствора отводится через патрубок 3.
Результаты исследования и их обсуждение
На начальном этапе проведен анализ объекта моделирования [1, 2]. Структурная схема процесса мембранного концентрирования представлена на рис. 2. Входным воздействием является концентрация задерживаемых веществ в исходном растворе С(S), % мас. Выходным параметром является удельная производительность по фильтрату G(S), м3/(м2?с). Основным каналом типа «вход – выход» является канал «исходная концентрация С(S) – удельная производительность G(S)», передаточные свойства которого описывает передаточная функция WС(S).
На процесс также оказывают влияние основные параметры технологического режима: рабочее давление p(S), температура концентрируемого раствора T(S). Передаточные свойства каждого канала системы определяются соответствующей передаточной функцией: канал «температура – удельная производительность» характеризуется передаточной функцией WТ(S), канал «давление – удельная производительность» передаточной функцией WР(S).
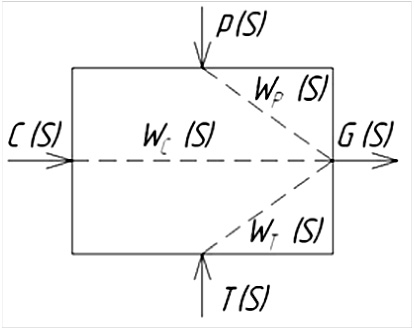
Рис. 2. Структурная схема процесса мембранного концентрирования
На этапе структурной идентификации установлено, что изменение удельной производительности под воздействием исходной концентрации наиболее точно описывает зависимость (1) [3, 4].
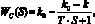 (1)
(1)
где k – коэффициент усиления объекта, м3/(м2·с); Т – постоянная времени объекта, с; k0 – удельная производительность по фильтрату в начальный момент времени, м3/(м2·с).
Изменение удельной производительности под воздействием температуры и давления наиболее точно описывают зависимости (2) и (3) соответственно [3, 4].
WT(S) = kT; (2)
Wp(S) = kp, (3)
где kТ – коэффициент влияния температуры концентрируемого раствора на удельную производительность по фильтрату, м3/(м2?с??С); kp – коэффициент влияния рабочего давления на удельную производительность по фильтрату, м3/(м2?с?МПа).
Вектор входных воздействий системы определен в виде
X(S) = {C(S), T(S), p(S)}. (4)
Характер изменения входного воздействия имеет ступенчатый вид, при этом величина в момент времени t0 мгновенно возрастает от начального Xнач до конечного Xкон постоянного значения и далее остается неизменной [3]. Такому воздействию соответствует функция
 (5)
(5)
На этапе параметрической идентификации по результатам экспериментальных исследований процесса мембранного концентрирования крахмального молока в ультрафильтрационном аппарате [6] установлены значения Xнач и Xкон входных воздействий
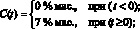 (6)
(6)
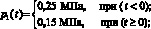 (7)
(7)
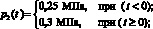 (8)
(8)
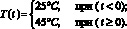 (9)
(9)
Для определения реакции системы на входные воздействия p1(t), p2(t), T(t) необходимо их совместное внесение в систему с воздействием С(t).
Экспериментально установлено, что коэффициент усиления k выражения (1) зависит от концентрации исходного сырья
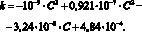 (10)
(10)
Параметрическая идентификация модели процесса мембранного концентрирования в ультрафильтрационном аппарате проводна на основе экспериментальных зависимостей (разгонных характеристик), полученных при внесении в систему выбранных воздействий.
Передаточные свойства канала «исходная концентрация С(S) – удельная производительность G(S)» описывает передаточ ная функция
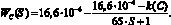 (11)
(11)
В диапазоне изменения давления от 0,15 до 0,25 МПа коэффициент влияния давления на удельную производительность составил
kp1 = –0,0009 % мас./(м2?с?МПа).
В диапазоне изменения давления от 0,25 до 0,3 МПа коэффициент влияния давления на удельную производительность составил
kp2 = 0,0012 % мас./(м2?с?МПа).
Влияние температуры на удельную производительность характеризуется коэффициентом усиления
kТ = 0,000007 % мас./(м2?с?°С).
Итоговая модель процесса мембранного концентрирования имеет вид
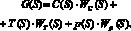 (12)
(12)
На заключительном этапе реализация математической модели программными средствами MatLAB позволила оценить ее адекватность экспериментальным данным. Расхождение экспериментальных и теоретических данных во всем диапазоне изменения технологических параметров процесса не превышает 4,8 %.
Таким образом, математическая модель процесса мембранного концентрирования в ультрафильтрационном аппарате с гидродинамическими элементами, разработанная на основе передаточных функций, с достаточной степенью адекватна экспериментальным данным и может быть использована для моделирования, расчета и прогнозирования работы мембранного оборудования.
Рецензенты:
Карташов В.Я., д.т.н., профессор кафедры прикладной математики, ФГБОУ ВПО «Кемеровский государственный университет», г. Кемерово;
Полтавцев В.И., д.т.н., профессор кафедры общенаучных дисциплин, ФГБОУ ВПО «Кемеровский государственный сельскохозяйственный институт», г. Кемерово.





