NEURAL NETWORK PREDICTIVE CONTROL FOR ROBOT DRIVE BASED ON TWO-MASSES MODEL WITH RESILIENCE
Dyda A.A. 1
Oskin D.A. 2
1 Admiral Nevelskoy Maritime State University
2 Far Eastern Federal University
Robot drive control problem based on two-masses model with resilience is considered in the paper. Considered mathematical model in traditional one and describes, in particular, a manipulator robot drive with resilient kinematics transmissions. Most results on solution of control synthesis problem for such dynamical objects are derived from nonlinear and adaptive control theory. The paper considers the two-masses system direct current drive with resilience and viscous friction. In this paper features of predictive neural network controller are investigated in comparison with conventional PID-regulator. Block diagrams of the electric drive control systems implemented in Simulink Matlab. It was demonstrated that application of predictive neurocontroller can essentially improve transient processes quality. Results of simulations are given and discussed.
industrial robot
two-mass electromechanical system
pid-control
neural network predictive control
1. Burdakov S.F., Djachenko V.A., Timofeev A.N. Proektirovanie manipuljatorov promyshlennyh robotov i robotizirovannyh kompleksov: uchebnoe posobie. M.: Vysshaja shkola, 1986. 264 р.
2. Zmeu K.V., Markov N.A., Notkin B.S. Prognozirujushhee inversnoe nejroupravlenie pozicionno-sledjashhim pnevmoprivodom // Informatika i sistemy upravlenija. 2011. 3(29). рр. 104–117.
3. Zmeu K.V., Markov N.A., Notkin B.S. Prognozirujushhee inversnoe nejroupravlenie pnevmoprivodom v uslovijah nekontroliruemyh vozmushhenij // Informatika i sistemy upravlenija. 2011. 4(30). рр. 116–123.
4. Zmeu K.V., Notkin B.S., Djachenko P.A. Bezmodelnoe prognozirujushhee nejroupravlenie // Mehatronika, avtomatizacija, upravlenie. 2006. no. 9. рр. 8–15.
5. Kljuchev V.I., Terehov V.M. Jelektroprivod i avtomatizacija obshhepromyshlennyh mehanizmov: uchebnik dlja vuzov. M.: Jenergija, 1980. 360 р.
6. Medvedev V.S., Potemkin V.G. Nejronnye seti. MATLAB 6 // pod obshh. red. V.G. Potemkina. M.: DIALOG-MIFI, 2002. 496 р.
7. Jurevich E.I. Osnovy robototehniki. 2-e izd., pererab. i dop. SPb.: BHV-Peterburg, 2005. 416 р.
8. Zmeu K.V., Notkin B.S., Stepaniuk V.V. Predictive Inverse Neurocontrol // Pacific Science Review Vol. 6 (1), 2004, Kokushikan University, Tokyo, Japan, pp. 22–25. ISSN 1229-5450.
Одним из важных направлений развития современной промышленности является создание автоматизированных производств, построенных на базе робототехнических систем. Задача автоматизации наиболее актуальна для технологических операций обработки деталей сложной конфигурации, в частности гидроабразивной резки гибких композитных материалов. Для эффективного решения задач автоматизации процессов обработки важная роль отводится промышленным работам (ПР). Одним из важнейших вопросов при автоматизации операций обработки является обеспечение требуемого качества обработки заготовки. В процессе механической обработки все звенья системы «робот – инструмент – деталь» (РИД) подвергаются воздействию силы резания, упругим колебаниям звеньев ПР, а также деформациям обрабатываемой поверхности, что приводит к колебаниям системы в общем. Наибольший вклад в колебания системы вносят упругие колебания манипулятора ПР, что связано с его большой податливостью. Упругие колебания отрицательно сказываются на работе робототехнического комплекса, вызывая увеличение динамических нагрузок на элементы, снижение быстродействия и точности при отработке программных траекторий, появление незатухающих вибраций, опасных резонансных явлений и т.п. Таким образом, для достижения требуемого качества обработки с точки зрения конструкции манипулятора ПР требуется решение задачи компенсации упругих деформаций манипулятора, возникающих под воздействием силы резания.
Существуют различные способы компенсации упругих деформаций. В литературе подробно описаны наиболее распространенные из них [1, 5, 7]. Одним из подходов является ограничение среднего ускорения электропривода, при этом увеличивается время переходного процесса привода, и это ведет к снижению производительности. Другим, альтернативным подходом является ограничение темпа нарастания динамического момента, при этом недостатки этого способа такие же, как и у первого.
Среди перспективных, активно развивающихся в последнее время подходов к управлению и дающих хорошие результаты можно предложить методы интеллектуального управления, основанные на использовании многослойных нейронных сетей или нечеткой (размытой) логики.
Целью работы являются исследования и сравнительный анализ традиционного управления с ПИД-регулятором и метода прогнозирующего нейроуправления скоростью двухмассового электромеханического объекта.
Математическое описание двухмассовой электромеханической системы
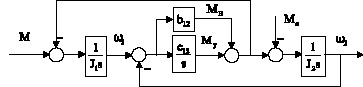
Рис. 1. Структурная схема двухмассовой механической системы
На рис. 1 приведена структурная схема двухмассовой механической части электромеханической системы [5]. На данной схеме все величины приведены к скорости вала двигателя и означают: J1 и J2 – момент инерции двигателя и механической передачи, приведенные к выходу передачи; w1 и w2 – их угловые скорости; c12 и b12 – эквивалентные коэффициенты жёсткости и вязкого трения упругого звена; M – момент двигателя; Mc – момент сопротивления. На структурной схеме обозначены:
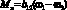 – момент вязкого трения;
– момент вязкого трения;
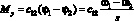 – момент упругой связи.
– момент упругой связи.
Математическое описание такой системы:
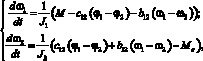 (1)
(1)
где ?1 – угол поворота вала двигателя, приведенный к выходу передачи; ?2 – угол поворота звена.
Прогнозирующее нейроуправление
Одним из развитых методов нейроуправления сложными динамическими объектами, такими как исполнительные устройства ПР, является прогнозирующее нейроуправление – Model Predictive Control (MPC) [2–4, 8]. В его основе лежит использование прогнозирующей модели процесса для прогнозирования (упреждения) поведения объекта управления в будущем. С использованием этой модели выполняется оптимизация программного управления, целью которого служит приближение выхода прогнозирующей модели к заданному.
Управление с прогнозированием использует подход, основанный на формировании управления на основании реакции нейросетевой модели управляемого объекта. Прогнозируемые значения используются программой численной оптимизации для того, чтобы вычислить управляющий сигнал, который минимизирует следующий критерий качества управления:
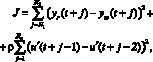 (2)
(2)
где константы N1, N2 и Nu задают пределы, внутри которых вычисляются ошибка слежения и величина управляющего сигнала. Переменная u? описывает пробный управляющий сигнал, yr – желаемая, а ym – истинная реакция модели объекта управления. Величина ? – весовой коэффициент, характеризующий вклад, который вносит управление в критерий качества.
Структурная схема на рис. 2 иллюстрирует процесс управления с прогнозированием. Регулятор состоит из нейросетевой модели управляемого процесса и блока оптимизации. Блок оптимизации определяет значения u?, которые минимизируют критерий качества управления, а соответствующий управляющий сигнал управляет процессом [6].
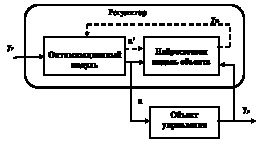
Рис. 2. Процесс управления с прогнозированием
Результаты моделирования
В работе рассмотрена двухмассовая система ЭП постоянного тока с упругой связью и вязким трением. Параметры двигателя (МИ-22): Uном = 60 В; Iном = 5,5 А; Pном = 250 Вт; nном = 2000 об/мин; Rя = 0,36 Ом; Lя = 2 мГн; Ja = 4?10–3 Нм2; Kem = 0,277; Kdv = Kem/Ra; Tdv = La/Ra. Параметры нагрузки, упругого сопротивления и вязкого трения: J2 = 6,67?10–4 Нм2; c12 = 1,1; b12 = 0,02. При постройке замкнутой системы предполагается, что контур регулирования скорости замкнут на первую массу (датчик скорости связан с валом приводного двигателя).
При моделировании настройка регулятора скорости произведена средствами автоматической настройки регулятора в среде Matlab Simulink (использовался ПИД-регулятор с ограничениями, наложенными на выходной сигнал) (рис. 3, а). Содержимое блока Model (модель двухмассовой системы) приведено на рис. 3, в.
Для сравнения с традиционной системой управления, основанной на применении классичесского ПИД-регулятора, рассмотрена нейросетевая прогнозирующая система (NN Predictive Controller) (рис. 3, б). Обучение нейрорегулятора проводилось по предварительно сформированной обучающей выборке (для объекта управления без учета второй массы). Параметры нейронной сети: четыре входных и выходных сигнала с шагом дискретизации 0,05 с, промежуточный слой представлен 10-ю нейронами. При формировании управляющих сигналов в нейрорегуляторе использовались настройки: N2 = 10; Nu = 2; r = 0,005; a = 0,01; Iteration Per Sample Time-2; Minimization Routine – csrchbac (поисковая функция одномерной оптимизации с обратной прогонкой).
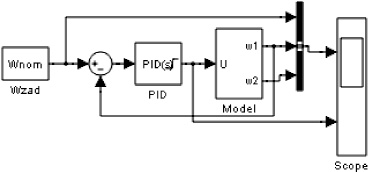
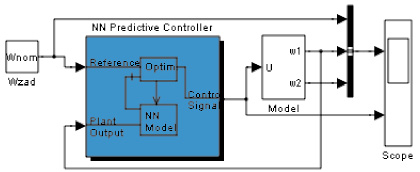
а б
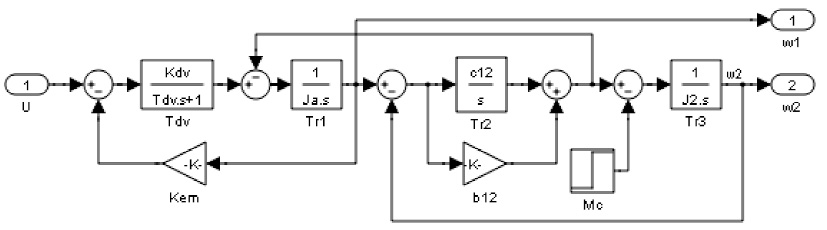
в
Рис. 3. Схемы Matlab Simulink, используемые при моделировании
На рис. 4 приведены управляющие сигналы, сформированные ПИД- и нейросетевым регуляторами. Как видно, нейросетевой регулятор работает в дискретном режиме, последовательно оптимизируя приведенный функционал качества (2).
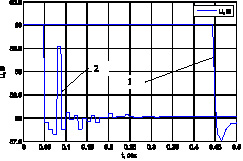
Рис. 4. Управляющий сигнал: 1 – в системе с ПИД-регулятором; 2 – в нейросетевой прогнозирующей системе
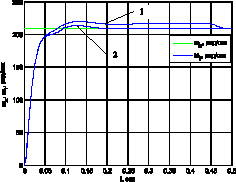
Рис. 5. Переходный процесс набора скорости 1-й массы: 1 – в системе с ПИД-регулятором; 2 – в нейросетевой прогнозирующей системе
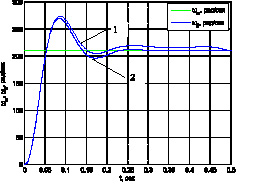
Рис. 6. Переходный процесс набора скорости 2-й массы: 1 – в системе с ПИД-регулятором; 2 – в нейросетевой прогнозирующей системе
Приведенные на рис. 5, 6 переходные процессы разгона первой и второй масс показывают преимущество использования нейрорегулятора, заключающееся в сокращении времени переходного процесса (с 0,475 до 0,2 с для первой массы, с 0,5 до 0,3 с для второй массы) и перерегулировании (с 31 до 28 % для второй массы).
Выводы
Применение прогнозирующего нейросетевого контроллера позволяет улучшить переходные процессы для скоростей двигателя и механизма в двухмассовой системе электропривода звена ПР.
Работа поддержана Министерством науки и образования Российской Федерации, Государственный контракт 02G25.31.0025.
Рецензенты:
Завьялов В.В., д.т.н., профессор кафедры технических средств судовождения, Морской государственный университет имени адмирала Г.И. Невельского, г. Владивосток;
Верёвкин В.Ф., д.т.н., профессор кафедры электрооборудования и автоматики судов, Морской государственный университет имени адмирала Г.И. Невельского, г. Владивосток.





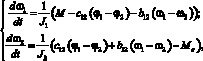 (1)
(1)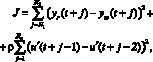 (2)
(2)





