THE NODAL METHOD OF ANALYSIS OF VIRTUAL PRIVATE NETWORKS
Gutkovskaya O.L. 1
Ponomarev D.Y. 1
1 FSBEI HPE «Siberian State Aerospace University named after academician M.F. Reshetnev», Krasnoyarsk
Providing Virtual Private Network (VPN – virtual private network) is an integral part of any telecommunications service provider. This service allows to connect remote branches of the company, as if between the branches was laid dedicated communication channel, in addition, provides quality of service guarantee for different types of network applications and traffic encryption mechanisms. One of the problems in the organization of VPN services is a choice of routes or topologies individual VPN networks, so as to date there is no routing protocol that would be built routes on the basis of quality of service parameters for each type of traffic, not to mention the VPN networks are at the second level of the OSI model. In connection with what the article proposed a method for obtaining the mathematical model of the distribution of traffic between the sites of virtual private networks based on tensor method. A feature of this method is the accounting process-structure interaction in the formation of a mathematical model of the distribution of information flows in VPN networks.
vpn networks
tenzor analysis of networks
traffic engineering
1. Gavlievskiy S. Metody analiza multiservisnyh setey svyazi s neskolkimi klassami obsluzhivaniya Dis. dok. tehn. nauk. [The methods for analysis of multiservice communication networks with multiple classes of service. Dr. techn. sci. diss]. Samara, 2012, 356 p.
2. Kron G. Tenzorniy analiz setey. [The Tensor analysis of networks]. Moscow, Sov.radio Publ., 1978, 719 p.
3. Petrov A. Tenzorniy metod dvoystvennyh setey. [The Method of dual tensor networks]. Moscow, Tsentr informatsionnyh tehnologiy v prirodopolzovanii Publ., 2007, 496 p.
4. Ponomarev D. [Packet networks characteristics research with using nodal method of tensor analysis]. Programmnye produkty i sistemy. 2009 No. 4, P. 65-69. Doi: 10.15827/0236-235X.
5. Roslyakov A. Virtualnye chastnye seti. Osnovy postroeniya i primeneniya. [The Virtual private network. Bases of construction and application]. Moscow, Eko-Trendz Publ., 2006, 304 p.
6. Rossiyskiy I zarubezhnyy rynok VPN i arendy kanalov: tekushee sostoyanie i perspektivy razvitiya [The Russian and foreign markets VPN and leased lines: current state and prospects of development]. (In Russ.). Available at: http://www.slideshare.net/kondrashov/ss-42552957 (accessed 23 June 2011).
Доля телекоммуникационного рынка от предоставления услуг VPN составляет порядка 6 %, а динамика роста данного сегмента рынка показывает ежегодный однопроцентный рост [6]. Основной технологией, в сторону которой осуществляется миграция услуги VPN, являются технология многопротокольной коммутации по меткам MPLS-VPN, а также техника двойной виртуальной локальной сети Q-in-Q и MAC-in-MAC. Применение той или иной технологии обусловлено масштабом VPN сети, для компании, чьи офисы расположены в рамках одного города провайдер, как правило, использует коммутаторы Ethernet второго уровня, что и определяет выбор технологии Q-in-Q или MAC-in-MAC. Филиалы предприятия, разнесенные по разным городам, соединяют между собой, используя технологию MPLS, так как на этом уровне используются, как правило, устройства третьего уровня. Обе технологии поддерживают механизмы качества обслуживания и возможность явного конфигурирования маршрутов. В рамках технологии Q-in-Q для управления потоками трафика можно как вручную задавать маршруты прохождения трафика, внося записи в таблицу коммутации, или же путем изменения параметров протокола STP (MSTP) и механизмов VLAN. В технологии MPLS управление маршрутами происходит путем явного указания маршрутов на граничных маршрутизаторах, а затем, используя протокол резервирования ресурсов RSVP-TE, происходит установка данного маршрута от одного граничного маршрутизатора до другого. Но какая бы технология ни была бы выбрана провайдером для организации VPN, необходим предварительный анализ, а по возможности и управления потоками трафика в сети провайдера с целью определения возможности предоставления услуги VPN с заданным качеством обслуживания.
Текущие методы анализа сетей VPN базируются либо на граф комбинаторных алгоритмов [5], либо на математическом аппарате теории массового обслуживания или сетей Маркова [1]. В данной статье предложен другой подход к получению математической модели сети VPN на основе тензорного анализа, согласно которому сеть можно рассматривать как совокупность геометрических объектов в пространстве, размерность которого определяется топологией сети. Преимуществом данного подхода является простота алгоритма получения математической модели, описывающей состояние сети в виде системы линейных уравнений, решение которых в зависимости от накладываемых ограничений обеспечивает оптимальное распределение трафика между сайтами VPN сети.
Постановка задачи
Исходными данными для анализа VPN сети служит топология сети провайдера, предоставляющего услуги VPN, матрица запросов между отдельными сайтами VPN, потоки между сайтами VPN, как правило, задаются в виде матрицы запросов, представляющей собой матрицу размерности DxD, где элемент dij – показывает интенсивность потока от i-го сайта до j-го сайта одной сети VPN.
Анализируемыми характеристиками являются потоки трафика и загрузка каналов связи при ограничениях на параметры качества обслуживания. В результате анализа будут предложены маршруты прохождения трафика между каждой парой сайтов. Пусть топология сети провайдера представлена в виде ориентированного графа G(N,A), где каждое ребро графа определяет однонаправленный канал связи. Как известно из теории массового обслуживания, в качестве математической модели однонаправленного двухточечного канала связи может выступать одноканальная система массового обслуживания, так как алгоритм обслуживания пакетов в интерфейсе маршрутизатора/коммутатора соответствует модели обслуживания одноканальной СМО. Таким образом, в качестве модели всей сети выступает сеть массового обслуживания. Граф сети массового обслуживания может быть описан матрицей инцидентности I, каждый элемент которой равен –1 или 1 и показывает: входит или выходит ветвь i из узла j.
Общий подход к решению задачи узловым методом тензорного анализа
Основной идеей тензорного метода является то, что все топологии, содержащие одинаковое число ветвей, связаны между собой тензором преобразования, в роли которого может выступать матрица линейно-независимых разрезов или матрица линейно-независимых контуров, или объединенная матрица линейно-независимых контуров и разрезов.
Поскольку все сети с топологией, состоящей из одинакового числа ветвей, связаны между собой тензором преобразования, то среди множества проекций можно выделить так называемую примитивную сеть [2], примитивная сеть состоит из такого же количества ветвей, как и исследуемая сеть, но количество несвязанных компонент в ней также равно числу ветвей, в связи с чем потоки в каждой ветви примитивной сети оказываются независимыми. Топология примитивной узловой сети показана на рис. 1. Как видно, в примитивной узловой сети каждой узловой интенсивности соответствует интенсивность в соответствующей ветви. Под узловой интенсивностью можно понимать сумму потоков, втекающих или вытекающих из узлов.
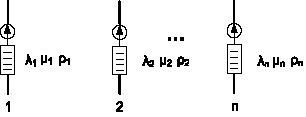
Рис. 1. Примитивная узловая сеть
Если определить математическую модель простейшего элемента сети, которым является одноканальная СМО, как ? = ??, то, согласно постулату обобщения Крона, если известна математическая модель, описывающая поведение простейшего элемента, то и система, состоящая из совокупности простейших элементов, будет описана такой же математической моделью, только в матричном виде. Следовательно, математическая модель примитивной сети имеет тривиальный вид и показывает связь узловых интенсивностей с узловыми временами обслуживания и узловыми загрузками.
(1)
где ?i (i = 1…n) – интенсивность поступления, поступающая на вход, элемента сети; µi (i = 1…n) – интенсивность обслуживания; ?i (i = 1…n) – загрузка i-го элемента.
Или в тензорном виде:
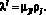(2)
Проблема тензорных преобразований по Г. Крону заключалась в том, что тензор преобразования между топологиями примитивной сети и анализируемой являлся сингулярной матрицей, что невозможно, так как тогда не существует обратного преобразования. В [3] введено понятие двойственных сетей и показано, что тензор преобразования осуществляет переход между парами двойственных сетей, а у Г. Крона рассматривается частный случай преобразований, где не учитывается возможность сингулярности.
Если в качестве базисных элементов для каждой топологии будут использоваться линейно-независимые разрезы, то тензор преобразования устанавливает связь между узловыми загрузками одной сети с узловыми загрузками другой сети, так связь узловых загрузок примитивной сети связана с узловыми загрузками исследуемой сети тензором преобразования А.
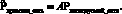
Количество узловых загрузок анализируемой сети определяется коциклическим числом, равным
p = n – 1,
где n – число узлов.
Тензор преобразования A определяется как матрица линейно-независимых разрезов, который в свою очередь равен матрице инцидентности без одной строки. Данный метод предполагает, что анализируемая сеть не содержит контуров, поэтому перед началом исследования сети ее необходимо преобразовать в узловую. Можно предложить два варианта преобразования сети с произвольной топологией в чисто узловую сеть. На рис. 2 показан первый вариант преобразования сети с произвольной топологией в контурную сеть с помощью разрыва узла. При этом необходимо отметить, что от узла отрываются только хорды.
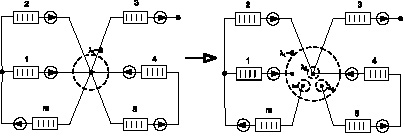
Рис. 2. Разрыв узла (первый вариант)
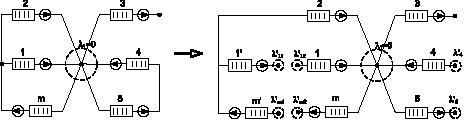
Второй вариант [4] предусматривает добавление дополнительных систем массового обслуживания, интенсивность обслуживания которых необходимо принять равную бесконечности, а интенсивность трафика, проходящего через нее, необходимо оставить такой же, как в той СМО, которую данная СМО дополняет. На рис. 3 показан второй способ преобразования сети в чисто узловую.
Как видно из рис. 3, дополнительные СМО помечены штрихами, количество дополнительных СМО определяется числом хорд графа, которые инцидентны узлам, соединяющим более двух ветвей (рис. 3, а). Необходимо отметить, что преобразование в узловую сеть эквивалентно увеличению размерности матрицы инцидентности, в первом случае добавляются только новые узлы, т.е. добавляются дополнительные строки, а во втором случае добавляются и новые ветви, что эквивалентно еще и добавлением столбцов. Более рациональный подход к преобразованию произвольной сети к чисто узловому виду показан на рис. 3, б, рациональность заключается в том, что контура лучше разрывать в узлах, которым инцидентны только два ребра, так как при этом не добавляются дополнительные СМО, если разрыв необходимо сделать в узле, которому инцидентны более двух ветвей, то в этом случае необходимо добавить дополнительные СМО. Использование первого метода обеспечивает минимум преобразований над сетью, то есть матрица инцидентности, которой была задана исходная сеть, будет преобразована в новую матрицу путем добавления стольких строк, сколько было сделано разрывов. Во втором варианте в матрице инцидентности появляются не только строки, обусловленные появлением новых узлов, но и столбцы, которые отражают появление дополнительных ребер. Но в связи с тем, что число ветвей, инцидентных узлам, принадлежащим не преобразованной сети, остается не неизменным, то после преобразования сумма потоков в узлах, которым инцидентны два и более ребра, остается равной нулю, что приведет к более простому виду матрицы узловых интенсивностей поступления, полученной по формуле (4).
Связь узловых загрузок примитивной сети с исследуемой можно, как уже было сказано, записать следующим образом:
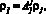(3)
где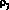 
– узловые загрузки примитивной сети; 
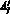– тензор преобразования узловых загрузок исследуемой сети в узловые интенсивности примитивной сети; ?j – значение узловых загрузок исследуемой сети.
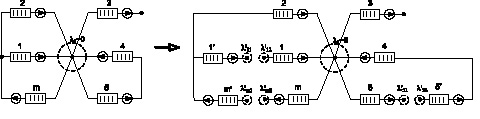
а
б
Рис. 3. Разрыв узла (второй вариант)
С помощью несложных матричных преобразований можно показать, что
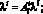(4)
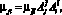(5)
где ?i – вектор узловых интенсивностей поступления исследуемой сети; 
– вектор узловых интенсивностей поступления примитивной сети; ?ji – матрица узловых интенсивностей обслуживания исследуемой сети;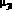 
– матрица узловых интенсивностей обслуживания примитивной сети.
На основании полученных значений узловых интенсивностей поступления и узловых интенсивностей обслуживания значения узловых загрузок исследуемой сети будут определяться как
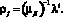(6)
А значение загрузок в каждой ветви можно определить следующим образом:
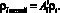(7)
Поскольку для каждой сети VPN известны свои матрицы запросов, проводя тензорный анализ характеристик для каждой VPN сети по отдельности, тем самым получив столько систем уравнений типа (7), сколько существует сетей VPN, затем, просуммировав одноименные строки всех уравнений, получается финальная система уравнений, отражающая зависимость интенсивностей потоков в каждом канале связи от загрузок, создаваемой каждой отдельной сетью VPN. Таким образом, если число сетей VPN равно N, то окончательная система уравнений, определяющая потоки всех VPN сетей в каждой ветви исследуемой сети, будет следующей:
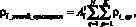(8)
где ?i_qp – вектор узловых загрузок, создаваемая p-м сайтом q-й VPN сети.
Система уравнений (8) содержит n уравнений, где n – число ветвей в анализируемой сети, а число неизвестных равно S?p, где S – общее число сайтов всех VPN сетей. Следовательно, система уравнений (8) имеет бесконечное число решений, это связано с тем, что каждое решение системы уравнений определяет какой-либо маршрут прохождения трафика между сайтами VPN сетей, а поскольку вариантов прохождения маршрутов существует бесконечное множество, то и система уравнений имеет бесконечное число решений. Систему уравнений (8) можно использовать для анализа трафика VPN двумя способами. Первый вариант вытекает из того, что в системе (8) загрузки в каждой ветви выражаются через линейно-независимые интенсивности поступления, поэтому, определив потоки/загрузки только в линейно-независимых ветвях, автоматически определяются и потоки/загрузки в оставшихся ветвях. Второй вариант использования системы уравнений (8) заключается в отыскании какого-либо решения, а не в подборе значений линейно-независимых компонент, при этом полученное решение будет описывать маршруты межу сайтами VPN, но при таком подходе система уравнений (8) должна решаться с рядом обязательных ограничений в виде системы неравенств. Обязательным ограничением для сиcтемы уравнений (8) является не отрицательность потоков создаваемой отдельным сайтом q-ой VPN сети, значение суммарного потока в канале связи не должно превышать величину пропускной способности данного канала, величина потока в ветви n от p-го сайта q-й VPN не должна превышать величину потока создаваемую p-м сайтом q-й VPN сети, а также обеспечить отсутствие появления петлевых маршрутов. Дополнительными ограничениями, накладываемыми на систему уравнений (7), могут быть ограничения сквозной задержки или вероятности потерь каждого типа трафика, создаваемого сайтами VPN сетей.
Таким образом, решая систему уравнений (8) с учетом неотрицательности потоков или другими ограничениями, накладываемыми на качество обслуживания потоков сетей VPN, а также учитывая значения матриц запросов, можно однозначно определять маршруты прохождения трафика между сайтами VPN сетей. В свою очередь, если решение системы уравнений (8) совместно с накладываемыми ограничениями найти не удается, то это означает, что данная сеть не может передать то количество трафика, которое генерируется каждой VPN сетью с требуемым качеством обслуживания.
Численные результаты
В качестве примера проведем анализ сети VPN, приведённой на рис. 4.
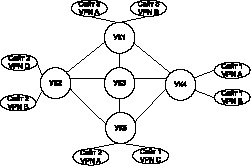
Рис. 4. Пример организации сети VPN
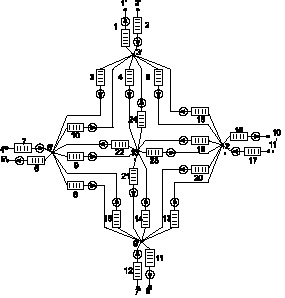
Рис. 5. Сеть массового обслуживания для исследуемой сети
На рис. 4 УК – это узел коммутации, в роли которого, как правило, выступают маршрутизаторы или коммутаторы.
Сеть массового обслуживания как математическая модель анализируемой сети будет иметь вид, представленный на рис. 5.
В соответствии с узловым методом анализа узлы 1?, 2?, 4?, 5?, 7?, 8?, 10?, 11? объединяются в один разрез, после определяется тензор преобразования от структуры исследуемой сети к структуре примитивной сети, который связывает узловые загрузки исследуемой сети с узловыми загрузками примитивной. Затем по формулам (4) и (5) определяются узловые интенсивности поступления и узловые интенсивности обслуживания. После чего определяются узловые загрузки анализируемой сети по формуле (6), затем по формуле (7) определяются загрузки в каждой ветви, создаваемые p-м сайтом q-й VPN, затем по формуле (8) определяются загрузки в каждой ветви, создаваемые всеми сайтами.
Если предположить что матрицы запросов для такой сети будут иметь следующий вид:
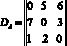– матрица запросов для сайтов VPN A;
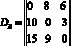– матрица запросов для сайтов VPN B;
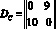– матрица запросов для сайтов VPN C.
Элементы матриц показывают, сколько единиц информации в секунду передается от i-го сайта к j-му, в рамках одной VPN, так элемент матрицы DA, находящийся в первой стоке и втором столбце, показывает что из первого сайта во второй сайт VPN А будет передаваться 5 ед. инф./с. Время обслуживания одной единицы информации принято как 0,01 с или 100 пакетов в секунду. При таких матрицах запросов одним из решений системы уравнений (8) соответствует следующее распределение загрузок по ветвям:
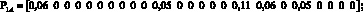
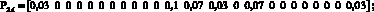
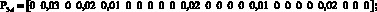
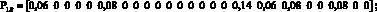
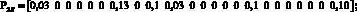
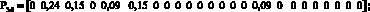
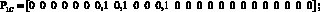
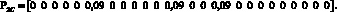
Каждый вектор показывает, какие загрузки в ветвях создаются p-м сайтом VPN_q. Суммарный вектор загрузок для каждой ветви показан ниже:
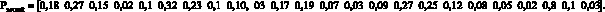
Также при решении данной задачи в качестве ограничений выступало то, что значения элементов векторов ?ij и ?ветвей должны находиться в диапазоне [0; 1). Таким образом, полученное решение удовлетворяет поставленным ограничениям, при этом необходимо отметить, что это одно из множества решений.
Заключение
В данной статье был представлен метод исследования сетей VPN c использованием узлового метода анализа. В связи с тем, что сетевая структура многих организаций строится именно на базе сетей VPN, провайдеры, предоставляющие данный вид услуг, должны обеспечивать гарантии по качеству обслуживания потоков трафика для каждой VPN. Большое количество поддерживаемых сайтов VPN и разветвленная инфраструктура сети провайдера делают задачу управления потоками трафика достаточно рутинной, в свою очередь, предложенный метод анализа очень хорошо описывает распределения трафика в больших системах благодаря хорошо формализованному матричному математическому аппарату, который остается инвариантным к размеру исследуемой топологии. Также необходимо отметить, что арифметические операции, производимые над матрицами, являются хорошо распараллеливаемыми вычислительными операциями, что позволит на многопроцессорных системах сократить время анализа сетей VPN. Преимуществами данного подхода по сравнению с существующими методами является простота получения математической модели, сложность вычисления маршрутов между сайтами VPN растет линейно с увеличением числа каналов в сети провайдера, в случае если необходимо провести анализ возможности организации маршрута по конкретным ветвям сети. Но если стоит задача в поиске произвольного маршрута, который будет являться решением системы уравнения (8), то накладываемое ограничение на отсутствие маршрутных петель в каждом маршруте между сайтами VPN увеличивает сложность задачи. Также необходимо отметить, что вид тензора преобразования узловых загрузок полностью определяется матрицей разрезов исследуемой сети.
Рецензенты:
Петров М.Н., д.т.н., профессор, зав. кафедрой ЭТТ, Сибирский государственный аэрокосмический университет им. акад. М.Ф. Решетнева, г. Красноярск;
Малинкин В.Б., д.т.н., профессор кафедры МЭС и ОС, Сибирский государственный университет телекоммуникаций и информатики, г. Новосибирск.
