В настоящее время, когда финансирование научных исследований и разработок происходит на конкурсной основе, встает задача не только идентификации перспективных научных направлений, но и определение значимости научных результатов тех творческих коллективов, которые могут претендовать на такую поддержку.
Научное (научно-техническое) направление характеризуется совокупностью научных работ, объединенных общностью объекта и методов исследования, общностью тем и их взаимосвязанностью. К научным работам или, более точно, научным результатам (НР) мы относим тезисы докладов, статьи, монографии и учебники, препринты, защищенные диссертации и результаты интеллектуальной деятельности (патенты на изобретения, промышленные образцы, полезные модели и селекционные достижения, свидетельства государственной регистрации на программы для ЭВМ и базы данных).
Стандартная модель жизненного цикла научного направления предполагает четыре этапа своего развития: зарождение, рост, зрелость и насыщение с последующим распадом [3]. Этапы зарождения и роста составляют интенсивную фазу, а этапы зрелости и насыщения – экстенсивную. Во время первой, интенсивной фазы, число ежегодно получаемых принципиально новых научных результатов быстро увеличивается, на экстенсивной – падает. По длительности интенсивная стадия познания заметно короче, чем экстенсивная. На разных этапах жизненного цикла преобладают разные виды научных результатов. Так, на первом этапе развития научного направления преобладают фундаментальные исследования, на второй – прикладные исследования и разработки. В соответствии с этим изменяется основной вид результатов научной деятельности в сторону увеличения патентов и свидетельств.
Объем накопленной в мире научной информации (тезисы, статьи, монографии, патенты и т.д.) оценивается в петабайтах (большие данные, Big Data) и требует специальных методов обработки. Современные мировые базы данных имеют свои собственные классификаторы научных направлений. Использование имеющихся классификаторов также сопряжено с рядом трудностей. Во-первых, эти классификаторы отличаются друг от друга, во-вторых, динамика изменения направления прикладных исследований чрезвычайно высока, и классификаторы не успевают изменяться так быстро, как нужно. В-третьих, появление нового научного направления не всегда бывает замечено и отражено в классификаторах. Например, в [1] приведены результаты исследования списка предметных кодов JEL в электронной библиографии экономической литературы EconLit. По данным 2006–2013 годов выявлены 62 новых направления экономических исследований на пересечении микрообластей классификатора JEL.
Таким образом, решение задачи многомерной классификации на больших объемах научных данных является весьма актуальным.
Состояние вопроса
Постановка задачи классификации выглядит следующим образом.
Пусть есть множество объектов X, заданных в многомерном пространстве признаков, и конечный набор классов {Ci ... Cn}. Известно, что каждый объект x ? X относится к некоторому классу Cj ? {C1, C2, ... Cn}. Таким образом, необходимо построить правило (алгоритм) отображения каждого объекта из Х к своему классу T:X ? {C1, C2, ... Cn} с наибольшей точностью.
Учитывая, что реальное пространство признаков очень велико и разрежено, а самих объектов чрезвычайно много, то подгонка параметров алгоритма (его обучение) проводится по некоторому конечному подмножеству XL ? X, называемому обучающей выборкой.
Для решения задачи построения классификатора наилучшей точности, сохраняющего при этом хорошую обобщающую способность на больших данных, могут быть использованы различные алгоритмы. Рассмотрим несколько алгоритмов, хорошо зарекомендовавших себя при работе с большими данными.
Наивный байесовский классификатор (NA?VE BAYES, NB). Наивный байесовский классификатор объединяет модель с правилом решения. Одно общее правило должно выбрать наиболее вероятную гипотезу; оно известно как апостериорное правило принятия решения (MAP). Соответствующий классификатор – это функция {classify}, определённая следующим образом [2]:
![]()
где f1, f2, …, fn – переменные (характеристики объекта); С – класс.
То есть вероятность принадлежности объекта к конкретному классу рассчитывается как произведение вероятностей независимых событий о равенстве переменных конкретным значениям для класса.
К достоинствам алгоритма относятся такие свойства, как устойчивость к изолированным точкам шума; обработка как количественных, так и дискретных данных, быстрое вычисление и эффективное использование памяти, нечувствительность к нерелевантным переменным. При работе алгоритма возникают проблемы, если условная вероятность равна нулю. Ограничением использования алгоритма является предположение, что переменные независимы.
Дерево решений (DT). Дерево принятия является одним из самых простых, но в то же время прозрачных и эффективных алгоритмов для выполнения классификации. Дерево решений представляет правила в иерархическом и последовательном виде, где каждому атрибуту соответствует свой узел, на основе которого дается решение [2].
К достоинствам данного алгоритма относится то, что он не требует предобработки данных, обладает высокой скоростью работы, высокой точностью и прозрачностью. Недостатком является то, что слишком сложные конструкции могут не отображать реальной картины, ввиду чего точность может оказаться ниже, чем у более простой конструкции
Лес деревьев решений (Random Forest, RF). Само по себе дерево решений не обеспечивает достаточной точности для этой задачи, но отличается быстротой построения. Алгоритм RF обучает k решающих деревьев на параметрах, случайно выбранных для каждого дерева, после чего на каждом из тестов проводится голосование среди обученного ансамбля. В основе построения этого алгоритма лежит идея о том, что если суммировать данные от большого количества различных слабых алгоритмов, сведя их в единый ответ, то результат, скорее всего, будет лучше, чем у одного мощного алгоритма [2].
Подобные алгоритмы обладают способностью эффективно обрабатывать данные с большим числом признаков и классов, мало чувствительны к масштабированию (и вообще к любым монотонным преобразованиям) значений признаков, одинаково хорошо обрабатываются как непрерывные, так и дискретные признаки, обладают внутренней оценкой способности модели к обобщению (тест out-of-bag), возможностью параллельной реализации и масштабируемостью. Существуют методы построения деревьев по данным с пропущенными значениями признаков и оценивания значимости отдельных признаков в модели. В качестве недостатков следует отметить, что алгоритм склонен к переобучению на некоторых задачах, особенно на зашумленных задачах, и требует большого объема памяти для представления полученных результатов. В этом случае требуется O(Nk) памяти для хранения модели, где k – число деревьев.
Совершенствование алгоритма классификации (Adaptive Boosting, AdaBoost).
Увеличение точности простых классификаторов может быть проведено путём комбинирования примитивных слабых классификаторов в один сильный алгоритм AdaBoost (от английских слов адаптивность и усиление) [7]. Под силой классификатора в данном случае подразумевается эффективность (качество) решения задачи классификации. Улучшение (Boosting) – это набор методов для порождения последовательности классификаторов, в которой каждый последующий классификатор пытается исправить ошибки предыдущих. Улучшение применяется к некоторому алгоритму классификации, называемому базовым классификатором (BaseLearner). Этот классификатор часто называют слабым классификатором. На каждом шаге алгоритм изменяет веса записей обучающей выборки, увеличивая веса неверно расклассифицированных записей.
Усиление происходит путем объединения их в комитет. Суть алгоритма заключается в комбинировании слабых классификаторов в один финальный, более мощный [7, 9]. Известно, что в качестве слабых классификаторов могут выступать практически любые, а использование комитетов почти всегда приводит к усилению результата [5]. В процессе обучения финального классификатора акцент делится на эталоны, которые распознаются хуже, т.е. выбирается классификатор, который лучше идентифицирует объекты, неверно распознанные предыдущим классификатором, в этом и заключается адаптивность алгоритма, в процессе обучения он подстраивается под наиболее сложные объекты.
Часто используются следующие способы построения комитетов алгоритмов [2, 4, 8].
1. Голосование по большинству (простое голосование), при котором комитет классификаторов относит объект к тому классу, к которому его отнесли большинство входящих в него алгоритмов.
2. Голосование по старшинству (машина покрывающих множеств). Этот метод предполагает последовательную одноклассовую классификацию. То есть первый алгоритм комитета отвечает за отнесение объекта к классу 1. Если он отказывается от классификации, то объект передается второму алгоритму, который может его отнести к классу 2. Если этого не произошло, объект передается к третьему классификатору и т.д., пока один из алгоритмов не при мет решения.
3. Взвешенное голосование из смеси экспертов. В этом случае голос каждого из классификаторов Ti, входящих в комитет Т, имеет свой вес ?i, зависящий от ошибки данного алгоритма на обучающем множестве:
![]()
В работе [6] приводятся данные, что усложнение правил построения комитетов, от взвешенного голосования до нейронных сетей, не дает значимого эффекта. Наилучший результат, повышение точности на 7–10 %, дает обучение комитета.
К достоинствам алгоритма AdaBoost следует отнести простоту реализации, возможность идентифицировать объекты, являющиеся шумовыми выбросами, хорошую обобщающую способность. В реальных задачах (не всегда, но часто) удаётся строить композиции, превосходящие по качеству базовые алгоритмы. Обобщающая способность может улучшаться (в некоторых задачах) по мере увеличения числа базовых алгоритмов. Время построения композиции практически полностью определяется временем обучения базовых алгоритмов.
К недостаткам алгоритма относятся следующие. Во-первых, AdaBoost склонен к переобучению при наличии значительного уровня шума в данных. Проблема решается путём удаления выбросов или применения менее агрессивных функций потерь. Во-вторых, жадная стратегия последовательного добавления приводит к построению неоптимального набора базовых алгоритмов. Для улучшения композиции можно периодически возвращаться к ранее построенным алгоритмам и обучать их заново. В-третьих, AdaBoost требует достаточно длинных обучающих выборок. Другие методы линейной коррекции, в частности бэггинг, способны строить алгоритмы сопоставимого качества по меньшим выборкам данных. В-четвертых, бустинг может приводить к построению громоздких композиций, состоящих из сотен алгоритмов. Такие композиции исключают возможность содержательной интерпретации, требуют больших объёмов памяти для хранения базовых алгоритмов и существенных затрат времени на вычисление классификаций.
Предлагаемый подход
Исходя из того, что каждый из описанных выше алгоритмов имеет свои плюсы и минусы по точности работы, наиболее рациональным решением можно считать сравнение результатов голосования каждого алгоритма и выбор того решения, за которое проголосовало большее количество алгоритмов.
Если за один класс проголосовало два и более алгоритма, то он признается правильным и фиксируется в системе. Если все алгоритмы проголосовали за разные классы, то приоритет отдается алгоритму лес деревьев по той причине, что он показал наибольшую точность на этапе тестирования алгоритмов (рис. 1).
Последовательность функций предложенного алгоритма следующая:
? загрузка и установка необходимых пакетов для обработки данных;
? импорт выборки данных и ее предобработка;
? выполнение кластеризации данных на основе алгоритма k-means;
? выполнение алгоритма дерево решений;
? выполнение алгоритма лес деревьев решений;
? выполнение алгоритма наивного байесовского классификатора;
? выполнение алгоритма голосующего комитета;
? оценка точности работы всех алгоритмов классификации.
Полученные результаты
Для тестирования алгоритмов классификации были использованы данные компании OttoGroup, которые имели обезличенный вид и находились в свободном доступе. Исходный файл с данными содержал 93 атрибута и 61878 объектов. Для формирования обучающей и тестовой выборки исходная выборка разбивалась в процентном соотношении 70:30.
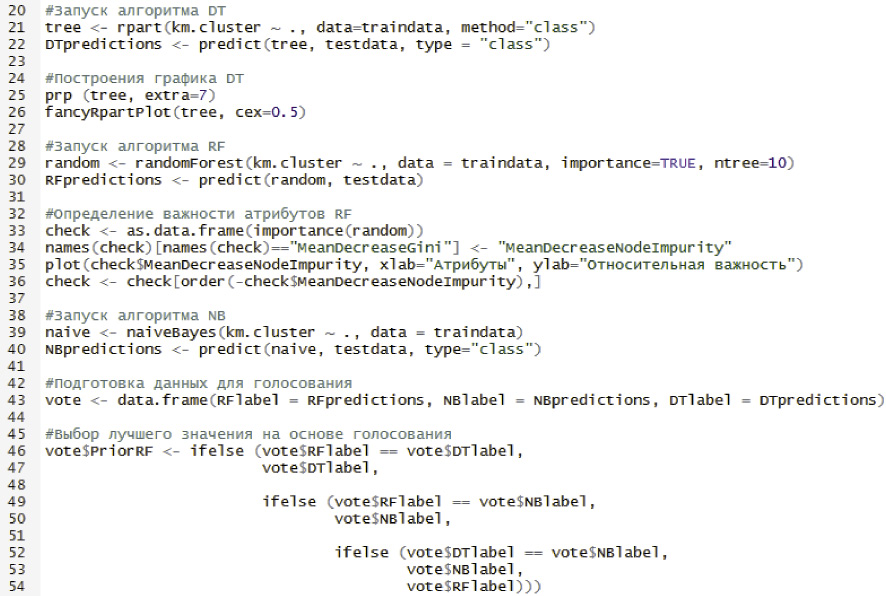
Рис. 1. Алгоритм голосований на языке R
Был проведен ряд экспериментов для определения точности классификации алгоритмов на различных объемах данных и для различных классов.
Параметры для тестирования имели следующий вид. Объем выборки составляли малые наборы (100 и 250), средние наборы (500 и 1500), большие наборы (500 и 15000). Количество классов составляло 4, 6 и 8. На основе указанных данных был проведен полнофакторный эксперимент.
Сводный результат по всем экспериментам представлен в табл. 1. Темным фоном выделены ячейки полученных результатов с большей точностью. Используемые обозначения алгоритмов:
? RF – лес деревьев решений;
? NB – наивный байесовский классификатор;
? DT – дерево решений;
? VT – комитет голосующих алгоритмов.
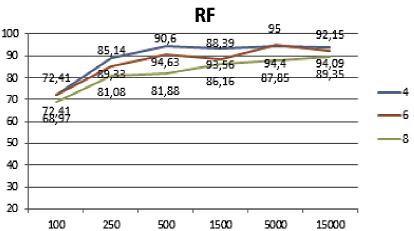
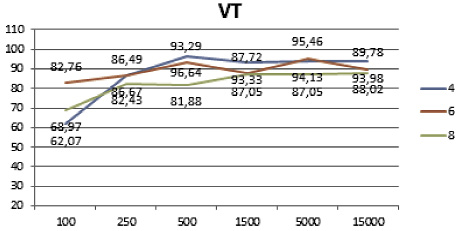
Полученные результаты классификации представлены на рис. 2 и 3. Из визуального представления полученных результатов классификации хорошо видно, что алгоритм лес деревьев решений лучше остальных отработал на большом наборе данных и на малом количестве классов (рис. 2). В свою очередь, комитет голосующих алгоритмов показал лучшие результаты на малых и средних наборах данных, а также на большом количестве классов (рис. 3).
Результаты сравнительного анализа точности полученных решений представлены в табл. 2. Исследование проводилось на выборках объемом 100 и 4 классах.
Таблица 1
Сводная таблица по всем экспериментам
|
DT |
NB |
|||||||
|
Выборка |
Классов |
Выборка |
Классов |
|||||
|
4 |
6 |
8 |
4 |
6 |
8 |
|||
|
100 |
58,62 |
79,31 |
44,83 |
100 |
37,93 |
31,03 |
27,59 |
|
|
250 |
82,67 |
72,97 |
81,08 |
250 |
65,33 |
32,43 |
27,03 |
|
|
500 |
91,28 |
93,96 |
71,81 |
500 |
47,65 |
42,95 |
32,21 |
|
|
1500 |
89,56 |
81,92 |
79,02 |
1500 |
74 |
73,66 |
49,78 |
|
|
5000 |
91,26 |
91,66 |
76,5 |
5000 |
83,52 |
52,37 |
56,48 |
|
|
15000 |
87,49 |
81,13 |
75,73 |
15000 |
85,04 |
67,68 |
61,57 |
|
|
RF |
VT |
|||||||
|
Выборка |
Классов |
Выборка |
Классов |
|||||
|
4 |
6 |
8 |
4 |
6 |
8 |
|||
|
100 |
72,41 |
72,41 |
68,97 |
100 |
62,07 |
82,76 |
68,97 |
|
|
250 |
89,33 |
85,14 |
81,08 |
250 |
86,67 |
86,49 |
82,43 |
|
|
500 |
94,63 |
90,6 |
81,88 |
500 |
96,64 |
93,29 |
81,88 |
|
|
1500 |
93,56 |
88,39 |
86,16 |
1500 |
93,33 |
87,72 |
87,05 |
|
|
5000 |
94,4 |
95 |
87,85 |
5000 |
94,13 |
95,46 |
87,05 |
|
|
15000 |
94,09 |
92,15 |
89,35 |
15000 |
93,98 |
89,78 |
88,02 |
|
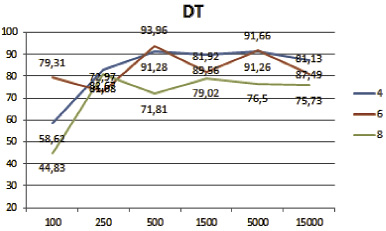
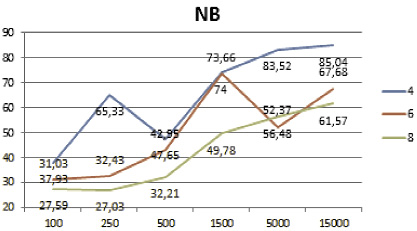
а б
Рис. 2. Результат классификации алгоритма: а – дерево решений; б – наивный байесовский классификатор