Для решения задач контроля всех этапов подготовки пуска, пуска ракет космического назначения (РКН), выведения полезной нагрузки на заданную орбиту и последующего управления КА в орбитальном полете на космодромах Российской Федерации применяются многофункциональные комплексы специальных средств, называемые измерительными комплексами космодрома (ИКК). Измерительный комплекс космодрома представляет собой сложную территориально распределенную организационно-техническую систему и предназначен для организации приема, регистрации, сбора, обработки и выдачи потребителям измерительной информации при подготовке к пускам, пусках и полете РКН, ракетных носителей (РН), запусках космических аппаратов (КА) и разгонных блоков (РБ), а также проведения сеансов управления КА в орбитальном полете.
Если ИКК используется только в целях обеспечения потребителей измерениями при подготовке к пускам, пусках и полете РКН и РН на активном участке траектории (АУТ), то в этом случае он выполняет функции полигонного измерительного комплекса (ПИК). При решении задач обеспечения потребителей измерениями на участке выведения на орбиту космической головной части (КГЧ), при орбитальном полете КА, а также для управления ими на всех этапах полета ИКК выполняет функции наземного комплекса управления (НКУ).
Совокупность бортового (БКУ) и наземного (НКУ) комплексов управления составляет автоматизированную систему управления (АСУ) космическими аппаратами [3]. В процессе активного функционирования КА осуществляется контроль и управление техническим состоянием как бортовых систем, так и наземных средств. Актуальной задачей является разработка математических моделей, позволяющих определять периоды контроля и управления техническим состоянием аппаратно-программных средств АСУ КА, обеспечивающие требуемую готовность к их применению.
Цель исследования – разработка математической модели, позволяющей определять оптимальную временную программу технического обслуживания средств сложной территориально распределенной организационно-технической системы.
Исходные предположения и допущения метода исследования
Процесс применения средств НКУ имеет циклический характер. Каждый цикл может включать в себя работу средства в номинальном режиме и нахождение в выключенном состоянии (режим «отдыха»). Диаграмма процесса применения наземных средств представлена на рис. 1.
Здесь ? – длительность цикла применения средства (например, одни сутки); t1 – длительность работы средства в номинальном режиме с коэффициентом нагрузки k = 1. При этом интенсивность его отказов имеет значение ?1.
На интервале t2 = ? – t1 средство находится в выключенном состоянии. Интенсивность отказов ?2 при этом, согласно [4], будет 0 ? ?2 ?? ?1.
Разработка модели
Для поддержания каждого средства в работоспособном состоянии периодически проводится его техническое обслуживание, на что затрачивается время ?обс. При этом выполняется углубленный контроль состояния в течение времени ?k1, проведение регламентных работ и восстановление работоспособности средства в случае обнаружения отказа, на что расходуется время ?в, а по окончании этих работ проводится контрольная проверка его работоспособности в течение времени ?k2. Контроль технического состояния выполняется в условиях номинального режима работы средства. Поэтому на интервалах времени ?k1 и ?k2 интенсивность отказов будет равной ?1. Для проведения ремонтно-восстановительных работ средство переводится в режим «отдыха», что соответствует интенсивности отказов ?2. В связи с этим общая продолжительность ?обс технического обслуживания выражается следующим образом [5]:
или
(1)
где P(T), P(?k1 + ?k2), P(?в) – вероятность безотказной работы средства на соответствующем интервале времени.
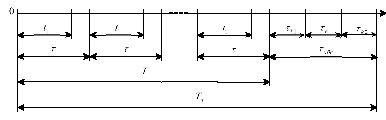
Рис. 1. Диаграмма процесса применения наземных средств
Длительность периода обслуживания T включает в себя множество 
циклов применения наземных средств с длительностью ? каждый, то есть
(2)
где 
(3)
Продолжительность Tц цикла обслуживания средства составляет
(4)
Вероятность безотказной работы средства на интервале времени T выражается так:
(5)
Для средств НКУ справедливо утверждение, что в них преобладают внезапные отказы и применим экспоненциальный закон распределения отказов [4]. При этом имеет место следующее:
(6)
(7)
Время работоспособного состояния средства Tф на интервале времени T определяется по формуле
(8)
Организация эксплуатации предусматривает определение рациональных или оптимальных, в некотором смысле, сроков технического обслуживания, обеспечивающих требуемое качество функционирования средств. Комплексным показателем качества является коэффициент технического использования (аналог коэффициента готовности). Его значение с учетом (4) и (8) выражается следующим соотношением:
(9)
Анализ функции Kг(T) показывает, что при T ? 0 и при T ? ? Kг(T) ? 0. Существует период технического обслуживания T*, при котором коэффициент Kг(T*) достигает максимального значения. Задача определения оптимального периода T* обслуживания средства выражается так:
(10)
Результаты исследования и их обсуждение
Рассмотренный подход целесообразно использовать применительно к отдельным, функционально обособленным средствам. В состав НКУ включается некоторое множество различных по функциональному назначению и безотказности средств. Каждому из этих средств соответствует индивидуальное оптимальное значение периода 
технического обслуживания. Множество значений 
, соответствующее множеству средств, включаемых в состав НКУ, 
, образуют такую совокупность циклов обслуживания, что практическая ее реализация является нерациональной. В связи с этим существует целесообразность упорядочивания этой совокупности путем нахождения компромиссных, близких к оптимальным, значений периода обслуживания всех средств НКУ. Такой компромисс является отражением решающего правила, которое вводится неформально и определяет собой допустимое отклонение значений периодов обслуживания средств от оптимальных 
значений. Конструктивной, с точки зрения упорядочивания сроков обслуживания средств является кратность периодов их обслуживания [5]. Различные средства (или группы средств) будут обслуживаться с различной периодичностью:
где 
– оптимальное значение периода обслуживания наименее надежного средства.
Решающее правило определения периода обслуживания каждого средства представляется так:
(11)
Условие (11) трансформируется в выбор для каждого средства некоторого допустимого значения коэффициента готовности 
, которое обеспечивает выполнение требования минимизации (11) и определяет границы допустимого значения 
периода обслуживания. Значение 
определяется из того, что коэффициент готовности средства будет не менее некоторого допустимого значения, то есть 
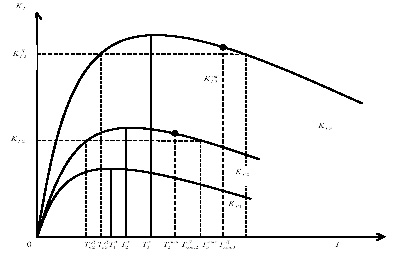
Рис. 2. Результаты численного эксперимента зависимости K?(T)
На рис. 2 в качестве примера показаны результаты численного эксперимента зависимости K?(T) для трех разнонадежных средств. Из данного примера видно, что некоторое отклонение значения K?i от максимального 
позволяет расширить область допустимых значений 
периода обслуживания. Значение 
можно определить как некоторую часть 0 < ? ? 1 от максимального значения, то есть 
. При этом 
не ограничивается только оптимальным значением 
, а будет находиться в интервале 
, где 
. Это позволяет вычислить значения периодов обслуживания 
средств, обеспечивающие функционирование этих средств с коэффициентом готовности 
. Предпочтительной для определения 
является область значений 
, ограниченная оптимальным значением 
и максимально допустимым 
, то есть 
. В этой области достигается требуемая готовность при большей периодичности обслуживания. Поскольку периоды обслуживания отдельных средств находятся из условия кратности, то этим обеспечивается рациональное в организационном плане обслуживание средств комплекса.
Выводы
В статье рассмотрены вопросы разработки математической модели определения оптимальных периодов управления техническим состоянием средств сложной организационно-технической системы. Система включает в себя совокупность средств, находящихся в связях, образующих целостность, единство. Существует план применения, включающий интервалы времени задействования системы по назначению и интервалы, в которых средства системы свободны от их применения (интервалы простоя). Организация эксплуатации предусматривает определение рациональных или оптимальных сроков технического обслуживания, обеспечивающих максимально возможную готовность средств к применению. Количественные показатели сложности, надежности и ремонтопригодности средств различны, поэтому и оптимальные периоды их обслуживания разные. В заявленной статье предложена математическая модель, позволяющая определять оптимальную временную программу технического обслуживания средств системы.
Рецензенты:
Миронов А.Н., д.т.н., профессор кафедры «Конструкции ракет-носителей и ракетных двигателей», ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского», г. Санкт-Петербург;
Павлов А.Н., д.т.н., доцент, профессор кафедры «Автоматизированные системы управления космических комплексов», ФГКВОУ ВПО «Военно-космическая академия имени А.Ф. Можайского», г. Санкт-Петербург.