Метод искусственных нейронных сетей является универсальным методом аппроксимации различных функций. Согласно теореме А.Н. Колмогорова [1], в которой утверждается, что каждая непрерывная функция n переменных, заданная на единичном кубе n-мерного пространства, представима в виде
(1)
где gi(y) – непрерывная функция; hi,j(xj) – непрерывная и стандартная функция, 
, 
, не зависящая от выбора аппроксимирующей функции f(x1, ..., xn)», практически любая функция может быть аппроксимирована нейронной сетью. В настоящей работе рассматривается использование метода искусственных нейронных сетей для решения задачи синтеза управления. Решением задачи синтеза управления для любого объекта является многомерная функция, определяющая значение вектора управления в зависимости от значения вектора состояния объекта управления.
Рассмотрим формальную постановку задачи синтеза управления [2].
Задана математическая модель объекта управления
(2)
где xi – компонента i вектора состояния x = [x1...xn]T; uj – компонента вектора управления u = [u1...um]T, m ? n.
Заданы ограничения на управление
(3)
Задано множество начальных состояний
(4)
Задана цель управления в виде терминального n–r-мерного многообразия
(5)
где tf – время управления, определяемое выполнением условия
(6)
t+ – заданное максимальное время процесса управления; ? – заданная малая положительная величина.
Задан критерий качества управления
(7)
где x(t, x0,j) – решение системы (2) с начальными условиями x0,j, 1 ? j ? M.
Необходимо найти управление с учетом ограничений (3) в виде
(8)
где
(9)
hi(x1, ..., xn) – искомая функция управления, 
.
Для решения задачи используем аппроксимацию искомой синтезирующей функции (9) многослойной искусственной нейронной сетью
(10)
(11)
(12)
(13)
…;
(14)
(15)
где
Q(k) – матрица весовых коэффициентов на слое k размерностью l(k)?p(k); 
N – число слоев в нейронной сети, p(1) = r; 
– функция активации нейронной сети на выходе i слоя k, 
Для обучения нейронной сети используем критерий (7). В процессе обучения необходимо найти
(16)
параметров.
Рассмотрим пример синтеза управления для нелинейной системы управления
(17)
(18)
Для системы (17), (18) задано множество начальных значений:
(19)
Заданы ограничения на управление:
–1 ? u ? 1. (20)
Задана цель управления в виде терминального многообразия:
(21)
(22)
где 
Задан критерий качества управления:
(23)
где 
j = 1, 2, 3, 4, t+ = 3 с, ? = 0,01. (24)
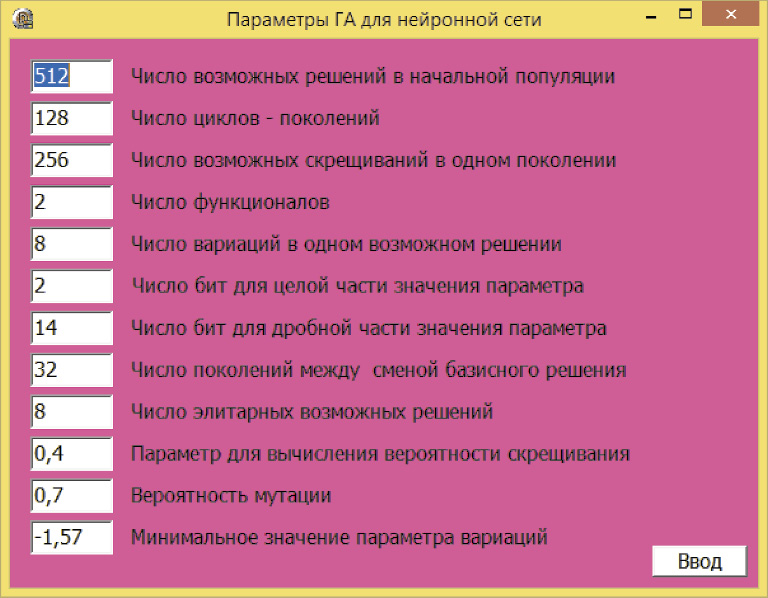
Рис. 1. Параметры вариационного генетического алгоритма для обучения нейронной сети
Для обучения нейронной сети используем вариационный генетический алгоритм [3]. Параметры генетического алгоритма приведены на рис. 1.
В результате была получена трехслойная нейронная сеть со следующими параметрами:
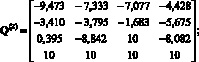
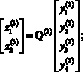
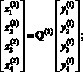
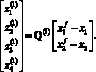
В процессе поиска нейронной сети при каждом вычислении функционала модель объекта управления (16), (17) интегрировалась улучшенным методом Эйлера второго порядка с шагом интегрирования 0,001 с.
На рис. 2 приведены решения замкнутой системы управления с полученной нейронной сетью в обратной связи и с учетом ограничений (8), (20).
На рис. 3 приведены решения замкнутой системы управления с полученной нейронной сетью в обратной связи для новых начальных условий, не используемых на этапе синтеза: x0,5 = [0 –1]T; x0,6 = [0 1]T; x0,7 = [1 0]T; x0,8 = [–1 0]T.
На рис. 4 приведены решения замкнутой системы управления с полученной нейронной сетью в обратной связи для начальных условий, расположенных дальше от терминальных условий, чем условия, используемые при синтезе: x0,9 = [–2 –2]T, x0,10 = [2 –2]T, x0,11 = [–2 2]T, x0,12 = [2 2]T.
На рис. 5 приведены решения замкнутой системы управления с полученной нейронной сетью в обратной связи для начальных условий, расположенных дальше от терминальных условий, чем условия, используемые при синтезе: x0,13 = [–2 0]T, x0,14 = [2 0]T, x0,15 = [0 –2]T, x0,16 = [0 2]T.
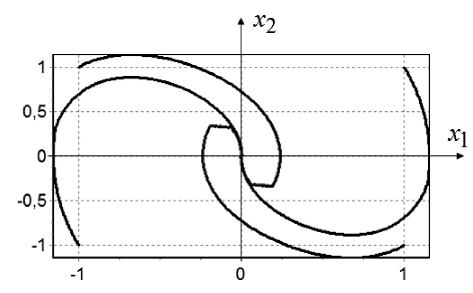
Рис. 2. Решения замкнутой системы Дуффинга для четырех начальных условий
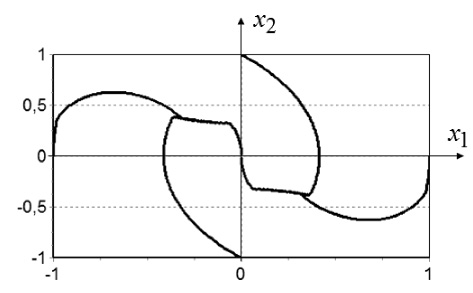
Рис. 3. Решения замкнутой системы Дуффинга для четырех не используемых при синтезе начальных условий
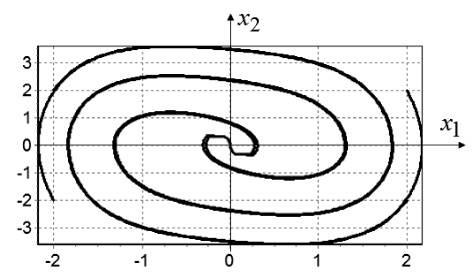
Рис. 4. Решения замкнутой системы Дуффинга для четырех не используемых при синтезе начальных условий: x0,9 = [–2 –2]T, x0,10 = [2 –2]T, x0,11 = [–2 2]T, x0,12 = [2 2]T
Как видно из графиков, представленных на рис. 2–5, полученная функция управления, аппроксимированная нейронной сетью, обеспечивает достижение терминального состояния из различных начальных условий.
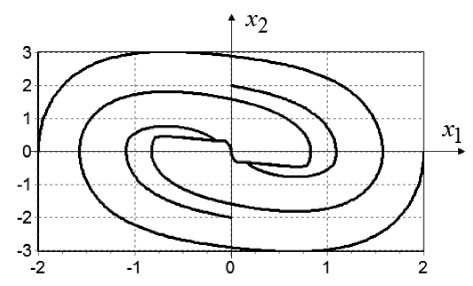
Рис. 5. Решения замкнутой системы Дуффинга для четырех не используемых при синтезе начальных условий: x0,13 = [–2 0]T, x0,14 = [2 0]T, x0,15 = [0 –2]T, x0,16 = [0 2]T
В таблице приведены значения времени и точности достижения терминального состояния для различных начальных условий модели объекта.
Параметры качества управления
|
x1(0) |
x2(0) |
tf |
|
|
–1 |
–1 |
2,346 |
0,009253 |
|
–1 |
1 |
2,585 |
0,009776 |
|
1 |
1 |
2,346 |
0,009253 |
|
1 |
–1 |
2,585 |
0,009776 |
|
0 |
–1 |
2,254 |
0,009293 |
|
0 |
1 |
2,254 |
0,009293 |
|
1 |
0 |
2,481 |
0,009246 |
|
–1 |
0 |
2,481 |
0,009246 |
|
–2 |
–2 |
5,73 |
0,009905 |
|
2 |
–2 |
5,805 |
0,009868 |
|
–2 |
2 |
5,805 |
0,009868 |
|
2 |
2 |
5,73 |
0,009905 |
|
–2 |
0 |
5,901 |
0,009408 |
|
2 |
0 |
5,901 |
0,009408 |
|
0 |
–2 |
3,205 |
0,009114 |
|
0 |
2 |
3,205 |
0,009114 |
Значения в таблице показывают, что объект управления достигает терминального состояния с заданной точностью, не превышающей 0,001.
На рис. 6–9 приведены графики значений управления для различных начальных состояний.
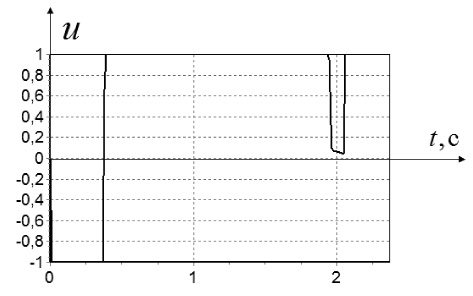
Рис. 6. Значение управления при начальных условиях: x0,3 = [1 1]T
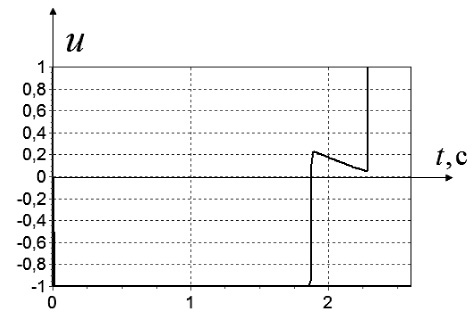
Рис. 7. Значение управления при начальных условиях: x0,2 = [–1 1]T
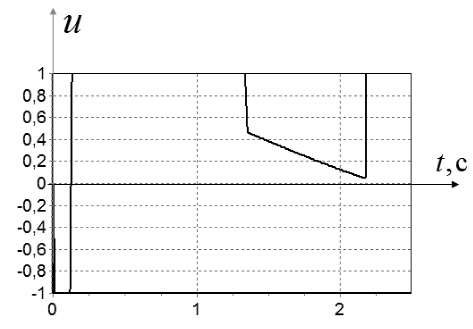
Рис. 8. Значение управления при начальных условиях: x0,7 = [1 0]T
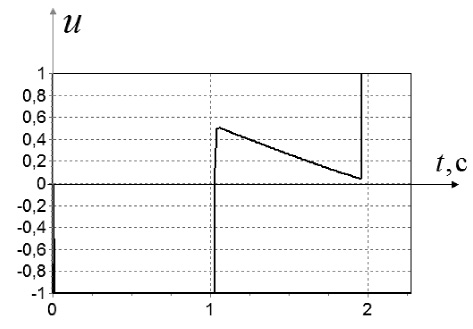
Рис. 9. Значение управления при начальных условиях: x0,6 = [0 1]T
Из рис. 6–9 видно, что управление носит обычный для задач быстродействия переключающий характер между предельными значениями.
Рецензенты:
Беляев В.В., д.т.н., профессор, начальник отдела развития науки, Московский государственный областной университет, г. Москва;
Прокопьев И.В., д.т.н., старший научный сотрудник федерального исследовательского центра «Информатика и управление», г. Москва.