Процесс урбанизации характеризуется не только ростом уровня жизни и производительности, но и возникновением экологических угроз, которые могут обесценить достигнутые экономические и социальные результаты. В отличие от развитых стран, которые урбанизировались постепенно, что позволяло им отрабатывать модели роста методом проб и ошибок, развивающиеся страны в условиях быстрой урбанизации не имеют такой возможности и уже сейчас нуждаются в моделях, обеспечивающих экономический рост при снижении ущерба для окружающей среды и природных ресурсов. Для решения этой задачи используются индикаторы и рейтинги экологической эффективности [3].
Опираясь на концепции эко-эффективности и экологической результативности, авторы предложили подход к оценке экологической эффективности урбанизированных территорий, в соответствии с которым она определяется относительной экологичностью функционирования города в пределах экологической устойчивости природной среды и объемом мероприятий в сфере управления окружающей средой [2]. В русле данного подхода была разработана модель оценки экологической эффективности крупных городов [6, 7], которая прошла верификацию [5]. В результате апробации данной модели был получен рейтинг крупных городов России по значениям сводного индекса экологической эффективности за 2008, 2009 и 2011 гг. [6, 7] и выполнен анализ динамики частных и сводного индексов экологической эффективности [4].
Вместе с тем полученные оценки экологической эффективности крупных городов должны быть не только достоверными, но и количественно устойчивыми. Предполагается, что малые изменения значений исходных экологических индикаторов не должны приводить к качественному изменению значений сводного индекса экологической эффективности. Именно на оценку устойчивости (чувствительности) сводного индекса экологической эффективности крупных городов направлена данная работа.
Цель работы – разработать и апробировать алгоритм проверки устойчивости (чувствительности) оценок экологической эффективности крупных городов.
Методика расчета сводного индекса экологической эффективности крупных городов, рассмотренная в [6, 7], предусматривает следующий алгоритм.
Сводный индекс I экологической эффективности крупных городов рассчитывался по формуле
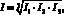(1)
где I1 – частный индекс экологической эффективности функционирования города; I2 – частный индекс экологической устойчивости; I3 – частный индекс эффективности управления окружающей средой.
Частный индекс экологической эффективности крупного города I1 «Экологическая эффективность функционирования города» рассчитывался по формуле
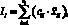(2)
где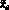 
(i = 1, 2, ..., sl) –i-е индикаторы экологической эффективности sl интегральной характеристики l (l = 1 – эффективность функционирования города), а ci – «веса» этих индикаторов, принятые равными. Частные индексы экологической устойчивости I2 и эффективности управления окружающей средой I3 представлены индикаторами экологической эффективности «Уровень загрязнения» (баллов) и «Доля текущих затрат на охрану окружающей среды в объеме промышленного производства» (%).
Исходные экологические индикаторы, характеризующие три составляющих экологической эффективности, включали:
1. «Экологическая эффективность функционирования города»:
x1.1 – Удельные выбросы вредных веществ в атмосферу от стационарных источников: всего на единицу объема промышленного производства (в сопоставимых ценах, 2009 = 1), т/руб.
x2.1 – Удельные выбросы вредных веществ в атмосферу от автомобильного транспорта: диоксид серы (SO2) на душу населения, кг/чел.
x3.1 – Удельные выбросы вредных веществ в атмосферу от автомобильного транспорта: оксиды азота (NO2) на душу населения, кг/чел.
x4.1 – Удельные выбросы вредных веществ в атмосферу от автомобильного транспорта: оксид углерода (CO) на душу населения, кг/чел.
x5.1 – Удельный сброс загрязненных сточных вод в поверхностные водные объекты на единицу объема промышленного производства (в сопоставимых ценах, 2009 = 1), тыс. тыс. куб. м/млн руб.
x6.1 – Вывезено спецтранспортом бытового мусора с территорий городов на душу населения, куб. м/чел.
x7.1 – Удельный вес площади зеленых насаждений в общей площади земель в пределах городской черты, %.
2. «Экологическая устойчивость»:
x8.2 – Уровень загрязнения, баллов.
3. «Эффективность управления окружающей средой»:
x9.3 – Доля текущих затрат на охрану окружающей среды в объеме промышленного производства, %.
Для оценки чувствительности сводного индекса экологической эффективности крупных городов к малым изменениям значений исходных экологических индикаторов предлагается использовать следующий алгоритм.
Задаются новые значения исходных экологических индикаторов с шагом, равным 1 % от медианы распределения значений соответствующего исходного экологического индикатора крупных городов в базовом году. Максимальное изменение задается равным 50 % от медианы.
Новые значения исходных экологических индикаторов рассчитываются по формуле
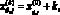(3)
где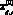 
– значение i-го ((i = 1, ..., 9) исходного экологического индикатора интегральной характеристики l (l = 1 – эффективность функционирования города; l = 2 – эффективность управления окружающей средой) для j-го (j = 1, ..., 31) крупного города в базовом году, k (k = 0,01?M(0), …, 0,05?M(0), …, 0,5?M(0)) – задаваемый шаг изменения значений 
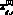, M(0) – медиана распределения значений 
.
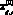Выбор медианы в качестве базы шага обусловлен стремлением получить одинаковые изменения значений исходного экологического индикатора для каждого крупного города. Среднее арифметическое не используется, поскольку вид распределения исходных экологических индикаторов неизвестен. Значения объема промышленного производства, численности населения крупного города и экологического индикатора «Уровень загрязнения» не изменяются. Изменение значений исходных экологических индикаторов может осуществляться по 4 сценариям: позитивному (значения x1.1, x2.1, x3.1, x4.1, x5.1, x6.1 снижаются, x7.1, x9.3 – растут), негативному (значения x1.1, x2.1, x3.1, x4.1, x5.1, x6.1 растут, x7.1, x9.3 – снижаются), «естественному» (значения x1.1, x2.1, x3.1, x4.1, x5.1, x6.1 снижаются, x7.1, x9.3 – снижаются), «препятствующему» (значения x1.1, x2.1, x3.1, x4.1, x5.1, x6.1 растут, x7.1, x9.3 – растут).
На каждом шаге k рассчитывается прирост сводного индекса экологической эффективности для каждого крупного города относительно его значения в базовом году по 4 сценариям:
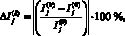(4)
где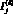 
– значение сводного индекса экологической эффективности j-го крупного города, построенного по новым значениям исходного экологического индикатор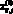а 
, а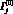 
– значение сводного индекса экологической эффективности j-го крупного города в базовом году.
Для наглядности и более детального анализа изменений на каждом шаге k рассчитывается относительный прирост сводного индекса экологической эффективности как медиана распределения прироста сводного индекса экологической эффективности в каждой из 3 групп крупных городов [4] (лидеры, «середняки», отстающие) по 4 сценариям:
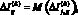(5)
где M – медиана;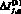 
– относительный прирост сводного индекса экологической эффективности для j-го крупного города, входящего в группу g (g = 1 – лидеры, 2 – «середняки», 3 – отстающие).
Используется медиана, а не среднее арифметическое, поскольку вид распределения относительного прироста сводного индекса экологической эффективности крупных городов неизвестен. Анализируется изменение значения медианы распределения относительного прироста сводного индекса экологической эффективности для каждой из трех групп крупных городов в зависимости от изменения исходных экологических индикаторов.
Для оценки устойчивости рейтинга крупных городов по сводному индексу экологической эффективности предлагается использовать ранговый коэффициент перестановок [1]:
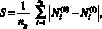(6)
где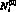 
– ранг (номер) i-го крупного города, входящего в группу g, в базовом рейтинге по сводному индексу экологической эффективности; 
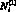– ранг (номер) i-го крупного города, входящего в группу g в новом рейтинге; g – номер группы крупных городов (g = 1 – лидеры, 2 – «середняки», 3 – отстающие).
Коэффициент (6) показывает, на сколько мест в рейтинге в среднем передвигается крупный город при задаваемых изменениях исходных экологических индикаторов. Чтобы глубже проанализировать происходящие трансформации с рейтингом при изменении значений исходных экологических индикаторов, целесообразно изучать поведение коэффициента (6) для каждой из 3 групп крупных городов (лидеров, «середняков», отстающих). Это позволит оценить, какая часть рейтинга более чувствительна к изменениям.
Тестировался предложенный алгоритм оценки чувствительности сводного индекса экологической эффективности крупных городов к малым изменениям значений исходных экологических индикаторов. При расчетах за базовый год был принят 2011 г. В качестве исходных экологических данных использовались официальные статистические данные Федеральной службы государственной статистики, Государственного учреждения «Главная геофизическая обсерватория им. А.И. Воейкова» [6, 7].
При использовании разных сценариев были получены схожие результаты. Для наглядности на рисунке представлен только негативный сценарий, поскольку именно при этом сценарии достигаются максимальные изменения значения сводного индекса экологической эффективности при изменении значений исходных экологических индикаторов.
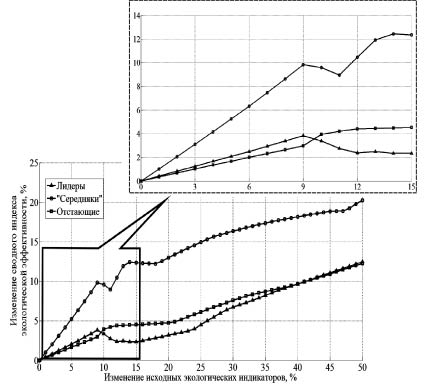
Медианы изменений сводного индекса экологической эффективности в зависимости от изменений исходных экологических индикаторов (негативный сценарий)