Известно, что большинство численных методов решения задач с фазовым переходом (задач Стефана) условно можно разделить на две группы: схемы сквозного счета и схемы с явным выделением фронта. Алгоритмы сквозного счета особенно широко применяются для многомерных задач, однако точность расчета как значения температуры, так и положения границы раздела фаз сильно зависит от параметра сглаживания, определить который часто довольно непросто.
Примером задачи Стефана является задача об образовании газовых гидратов при инжекции газа в пористую среду. Принципиальная особенность математической модели такой задачи состоит не только в учете фазовых переходов, но и массопереноса в пористой среде. Необходимость учитывать фильтрационные процессы (движение газа в пористой среде) усложняет задачу, поскольку, хотя она и сводится к задаче Стефана, но в отличие от классической задачи Стефана температура фазового перехода зависит от давления. Эта особенность является существенной, поскольку, как показано в работах [3–5], приводит к возникновению ситуации, когда фазовые переходы реализуются в протяженной области.
В данной работе для решения указанной задачи используется метод ловли фронта в узел пространственной сетки [1, 2].
Постановка задачи и основные уравнения
При описании процесса тепло- и массопереноса в пористых средах, сопровождающихся образованием гидрата при тепловом и депрессионном воздействиях, примем следующие допущения. Примем однотемпературную модель пористой среды. Будем также считать, что пористость среды постоянна, а ее скелет, гидрат и вода являются несжимаемыми и неподвижными, а газ – калорически совершенным. Гидрат является двухкомпонентной системой с массовой концентрацией газа G.
Рассмотрим горизонтальный пористый пласт протяженности L (0 ? x ? L), насыщенный в начальный момент времени водой (с объемным содержанием Sl = Sl0) и газом, давление р0 и температура Т0 которых соответствует условию существования их в свободном состоянии, т.е. Ts(p0) < Т0, где Ts(p0) – равновесная температура, соответствующая исходному давлению р0. Пусть через левую границу пористого пласта (х = 0) начинает закачиваться холодный газ (метан) с температурой Те (Те < Т0) и давлением ре, причем Те < Тs(ре), где Тs(ре) – равновесная температура, соответствующая давлению ре. Будем полагать, что в пласте образуются три области, в которых газ, гидрат и вода находятся в различных состояниях. Так в первой (ближней) области, примыкающей к левой границе пласта, вода полностью перешла в гидратное состояние, поэтому в порах присутствуют только газ и гидрат. Примыкающая к правой границе пласта третья (дальняя) область насыщена газом и водой, а промежуточная область, разделяющая между собой вышеуказанные области, содержит газ, гидрат и воду в состоянии термодинамического равновесия. При этом возникают две подвижные границы x = x(i) (i = n, d), разделяющие между собой указанные области, причем граница x = x(n) разделяет между собой ближнюю и промежуточную, а граница x = x(d) – дальнюю и промежуточную области.
Система уравнений тепло-и массопереноса, включающая в себя уравнения сохранения масс (воды и газа) и энергии, закон Дарси и уравнение состояния идеального газа, может быть представлена в виде [3–5]:
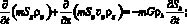
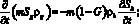
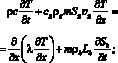(1)
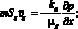p = ?gRgT.
Здесь и далее нижние индексы j = sk, h, l, g относятся к параметрам скелета, гидрата, воды и газа соответственно; t – время; m – пористость; Sj и ?j (j = sk, h, l, g) – насыщенности пор и истинные плотности j-й фазой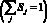 
; р – давление; Т – температура; vg – скорость газовой фазы, величины; Rg – приведенная газовая постоянная ?c и ? представляют собой удельную объемную теплоемкость и коэффициент теплопроводности системы «пористая среда – газогидрат»; Lh – удельная теплота гидратообразования; ps0 – равновесное давление, соответствующее исходной температуре, T* – эмпирический параметр, зависящий от вида гидрата; ?g – коэффициент динамической вязкости газа; kg – коэффициент проницаемости для газа, зависящий от текущей газонасыщенности на основе формулы Козени:
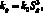
где k0 – абсолютная проницаемость пласта.
Кроме того, рассмотренные уравнения необходимо дополнить соотношениями на поверхностях разрыва между областями, в которых газ, гидрат и вода находятся в различных состояниях. На них терпят разрыв насыщенности фаз, а также потоки масс и тепла, выполняются следующие соотношения:
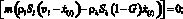
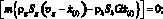(2)
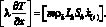
Здесь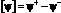 
– скачок параметра ?; 
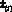– скорость движения границы x = x(i) (i = n, d); верхние знаки «плюс» и «минус» относятся к параметрам перед и за фронтом соответственно. Давление и температуру на обеих границах фазового перехода будем считать непрерывными величинами.
Так как в исходном состоянии пласт находится под давлением р0 и температурой Т0 с водонасыщенностью Sl0, то начальные условия можно записать в виде
p = p0; T = T0; Sl = Sl0 (0 ? x ? L, t = 0). (3)
Условия на левой границе (х = 0) можно представить в виде
p = pe; T = Te; (x = 0, t > 0). (4)
На правой границе пласта (x = L) поставим условия, моделирующие отсутствие через нее потока тепла и давление, равное начальному:
p = p0;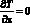 
(x = L, t > 0). (5)
Границу, на которой справедливы условия (5), будем называть открытой для потока газа.
Алгоритм численного решения задачи
Поскольку рассматриваемые задачи определены в областях с неизвестными подвижными границами фазовых переходов, то для их решения используется метод ловли фронтов в узлы пространственной сетки [1, 2]. Введем на отрезке равномерную пространственную сетку с шагом h: xi = ih,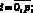 
x0 = 0, xp = L. На сегменте [0, t*] введем неравномерную сетку: tj+1 = tj + ?j+1, 
tj0 = t*, ?j > 0, где t* – конечный момент времени.
Алгоритм решения заключается в том, что неизвестный временной шаг ?j+1 выбирается таким образом, чтобы ближний фронт фазового перехода перемещался по координате х ровно на один шаг, т.е.
x(n)(tj+1) – x(n)(tj) = h.
При этом положение дальней подвижной поверхности x = x(d) также будем относить к некоторому узлу пространственной сетки, которое будет определяться уже в ходе решения задачи. Будем обозначать через n – узел пространственной сетки, соответствующий ближней границе x = x(n), а через d – узел, соответствующий границе x = x(d).
Уравнения пьезо- и теплопроводности, а также уравнение для определения гид ратонасыщенности, совместно с начальными и граничным условиями (1)–(5), представляются в виде неявных конечно-разностных соотношений [4]. При этом их решение на каждом временном слое осуществляется методом итераций, суть которого заключается в следующем. Пусть известны распределения основных параметров пласта на j-м временном слое. Для нахождения их значений на (j + 1)-м временном слое поступаем следующим образом. Задаем счетчику итераций значение s = 0, а также значения давления, температуры и временного шага на новом (j + 1)-м временном слое: (pi)s, (Tt)s, (?i)s. Увеличиваем счетчик итераций на единицу. При этом сначала из дискретного аналога системы уравнений (2) определяется «новое» значение гидратонасыщенности на ближней границе (Sh(n))s+1, а на основании (1) – «новые» значения гидратонасыщенности в промежуточной области. При этом очередное положение границы отнесем к узлу, в котором для значения гидратонасыщенности выполняется соотношение: (Sh,d)s+1 ? ?Sh, где ?Sh ? 0 при h ? 0. Затем методом прогонки относительно (pi)s+1 решается записанная в конечно-разностном виде система уравнений для давления (1) с учетом условий на границах фазовых переходов (2). Далее по найденным на «новой» итерации значениям гидратонасыщенности и давления методом прогонки решаются уравнения теплопроводности. Очередное приближение временного шага находим как среднее геометрическое
где ?1 и ?2 определяются из балансовых соотношений (2) на границе x = x(n). Процесс итераций на каждом временном слое продолжается до достижения заданной точности как по давлению, температуре, так и гидратонасыщенности, после чего переходим к рассмотрению очередного временного слоя.
Результаты расчетов
На рис. 1 для плоскоодномерного случая представлены распределения температуры и гидратонасыщенности при продувке пласта длины L = 2 м газом под давлением ре = 7 МПа температурой Те = 276 К. Начальные давление р0 = 3 МПа, температура Т0 = 280 К и водонасыщенность Sl0 = 0,2. Для остальных параметров, характеризующих систему, приняты следующие значения:
m = 0,1, G = 0,12,
T* = 10 К, ps0 = 5,5 МПа,
k0 = 10–13 м2, Rg = 520 Дж/(К?кг),
?h = 900 кг/м3, ?l = 1000 кг/м3,
cg = 1560 Дж/(К·кг),
?c = 2,5?106 Дж/(К·м3),
? = 2 Вт/(м?К), ?g = 10–5 кг(м?с),
удельная теплота гидратообразования Lh = 5·105 Дж/кг. При таких параметрах нагнетаемого газа образование гидрата в начальный момент времени происходит в протяженной области. Из рисунка следует, что с течением времени дальняя граница x = x(d) движется назад, навстречу ближней границе x = x(n). Действительно, в момент времени t = 1,2 ч координата дальней подвижной границы была равна x(d)1 ? 1 м, а в момент времени t = 4,4 ч – x(d)2 ? 0,8 м. При этом наблюдается падение значения гидратонасыщенности в этой области. Таким образом, в зоне трехфазного равновесия происходит частичное разложение ранее образовавшегося гидрата. Это обусловлено конвективным сносом нагретого газа за счет образования гидрата на границе x = x(n) и его течения в объемной области. В момент времени t = 15,3 ч процесс гидратообразования происходит уже на фронтальной поверхности x = x(n).
Рис. 1. Распределение температуры и гидратонасыщенности. Числа на кривых – время в часах
На рис. 2 представлена зависимость значения координат границ фазовых переходов от времени при продувке пласта газом. Сплошная линия соответствует параметрам на ближней границе x = x(n), а пунктирная – на дальней границе x = x(d). Из данного рисунка можно сделать вывод, что образование гидрата в режиме продувки происходит в три этапа. На первом, быстром по времени, автомодельном этапе, когда влияние правой границы пласта несущественно, в общем случае образуются три области, где газ, гидрат и вода находятся в различных состояниях. Здесь происходит движение вглубь пласта обеих границ фазовых переходов, при этом значения температуры и гидратонасыщенности на них остаются постоянными. На втором этапе происходит вырождение протяженной области во фронтальную поверхность, связанное с движением влево границы фазового перехода x = x(d). Это обусловлено конвективным сносом выделившегося тепла на границе x = x(n) и диссоциацией гидрата, образовавшегося на первом этапе. При таком перемещении влево границы x = x(d) процесс образования гидрата начинает стремиться к фронтальному, чем и обусловлено падение значений гидратонасыщенности на границе x = x(n). На третьем этапе процесс гидратообразования происходит лишь на фронтальной поверхности.
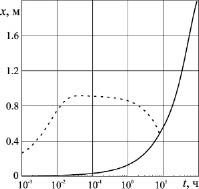
Рис. 2. Зависимость значений координат х = х(n) (сплошная линия) и х = х(d) (пунктирная линия) границ фазовых переходов при нагнетании газа
Выводы
Методом ловли фронта в узел сетки получено численное решение задачи об образовании гидрата в пористой среде. Установлено, что протяженная область фазовых переходов со временем может вырождаться во фронтальную по верхность.
Работа выполнена при финансовой поддержке РФФИ (грант 14-01-31089_мол-а).
Рецензенты:
Мустафина С.А., д.ф.-м.н., профессор, заведующая кафедрой математического моделирования, Стерлитамакский филиал, Башкирский государственный университет, г. Стерлитамак;
Биккулова Н.Н., д.ф.-м.н., профессор кафедры общей и теоретической физики, Стерлитамакский филиал, Башкирский государственный университет, г. Стерлитамак.