Моделирование динамики биологических сообществ имеет большое значение для их исследования. Фундаментальные работы [4, 5] дали толчок развитию математической экологии и математического моделирования динамики популяций. В этих работах популяция рассматривается с точки зрения химической кинетики, как своего рода химический реактор, в котором идут различные «химические» реакции (воспроизведение, смерть и другие виды взаимодействия организмов).
Большинство работ, посвященных моделированию динамики популяций, основываются на модели «реакция – диффузия». Такой подход предъявляет к особям достаточно жёсткие требования: особи должны передвигаться по пространству случайно и бесцельно особи не должны обладать памятью и, наконец, подавляющее большинство особей должны совершать малые перемещения в пространстве. Такие условия не выполняются ни для каких реальных биологических сообществ.
Для разрешения этих противоречий должен быть реализован новый класс моделей. Основной принцип, лежащий в их основе, состоит в том, что перемещение особей в пространстве должно удовлетворять условию эволюционной оптимальности и приводить к увеличению жизнеспособности популяции. Для этого особи должны перемещаться по пространству целенаправленно. Это означает, что при перемещении особи максимизируют некоторый показатель, описывающий популяцию в целом; им является коэффициент размножения – среднее на одну особь число потомком в достаточно длинной цепочке поколений [1, 2].
Мы будем рассматривать модель, основанную на эволюционной оптимальности, для пространственно распределенных одновидовых популяций, особи которых обладают различной степенью информированности. Модель глобально информированных особей предполагает, что особям известна вся информация о состоянии окружающей среды в месте их пребывания, а также в стации эмиграции, информация о численностях субпопуляций в обеих стациях и цена перемещения (т.е. затраты на перемещение из стации в стацию, выраженные в долях КР). Локальная информированность подразумевает, что особям известны условия окружающей среды и численность субпопуляции только в стации пребывания. Информацией о стации иммиграции особи не обладают. Кроме того, считаем, что для модели локальной информированности известна также цена перемещения из стации в стацию. Глобально и локально информированные особи принимают решение о миграции из стации в стацию на основании имеющейся и них информации. Здесь следует сделать одну важную оговорку. Строго говоря, миграция является не популяционным, а организменным эффектом: каждая особь индивидуально и самостоятельно принимает решение о том, мигрировать ей или нет. Однако в моделях, рассмотренных ниже, используется специальное приближение, в рамках которого акт миграции представлен популяционным механизмом: сперва определяется доля мигрантов, а затем происходит перераспределение особей между стациями, при этом способы отбора конкретных особей в мигранты не рассматриваются.
В данной работе мы выясним, как степень информированности влияет на динамику популяции.
Модель глобально информированных особей
Рассмотрим одновидовое сообщество, особи в котором распределены по двум стациям. Миграцией будет считаться только перемещение особей из одной стации в другую. Перемещения внутри стаций миграцией считаться не будут. Динамику популяции будем рассматривать в дискретном времени, один шаг по времени совпадает с циклом размножения.
Для описания динамики сообщества в каждой из стаций (в отсутствие миграции) будем использовать уравнение Ферхюльста:
Nt+1 = Nt?(a – bNt);
Nt+1 = Mt?(c – dNt), (1)
где Nt(Mt) – численность особей в момент времени t в I (соответственно, во II стации); коэффициенты a и c ? количество рождающихся особей, приходящихся на одну особь ? родителя, коэффициенты b и d описывают факторы саморегуляции, зависящие от плотности субпопуляции в стации. Выбор именно этого уравнения определяется двумя обстоятельствами: во-первых, это классическое уравнение математической экологии, и его применение позволит сделать результаты моделирования сравнимыми с другими, полученными ранее; во-вторых, это уравнение действительно применимо для описания динамики популяции, пусть и в специальной ситуации (вблизи порога выживания). Выражения в скобках будем называть коэффициентами размножения (КР) для первой и второй стации.
Определим, при каких условиях возникают миграционные потоки между стациями. Миграция происходит тогда и только тогда, когда условия существования в стации иммиграции оказываются лучше, чем в стации пребывания, с учетом цены перемещения p. Величина p (0 < p ? 1) описывает вероятность перемещения из стации в стацию без ущерба для дальнейшего размножения.
Условие возникновения миграционного потока из первой стации во вторую (из второй в первую) выглядит следующим образом:
a – bNt < p(c – dMt) (c – dMt < p(a – bNt) соответственно). (2)
При выполнении условия миграции нужно переместить такое количество особей ?, которое обратит неравенство (2) в равенство. Предполагаем, что выполняются очевидные условия: ? ? Nt (либо ? ? Mt). Если на каком-то шаге t условия миграции выполнены, то миграционный поток ? определяется одним из двух соотношений:
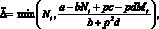
либо
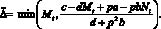 (3)
(3)
Особо отметим, что в модели глобально информированных особей миграционный поток на конкретном шаге по времени t может быть направлен только в одну сторону. Встречные потоки миграции отсутствуют.
Опишем теперь подробно, как работает модель. На каждом шаге времени t проверяются условия возникновения миграции, вычисляется величина миграционного потока ? и происходит перераспределение особей по стациям. Вычисляются новые численности 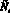 и
и 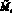 по следующим формулам:
по следующим формулам:
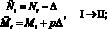
или
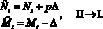 (4)
(4)
Для полученных численностей с учетом миграции 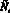 и
и 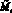 вычисляются численности на следующем шаге t + 1 по формуле (1).
вычисляются численности на следующем шаге t + 1 по формуле (1).
Модель локально информированных особей
В модели локально информированных особей также рассматривается одновидовое сообщество пространственно распределенных особей. Миграции определяются аналогично определению миграции для модели глобально информированных особей. Динамику популяции будем рассматривать в дискретном времени, один шаг по времени совпадает с циклом размножения.
Как было сказано выше, локальная информированность предполагает, что известны только условия существования «здесь». Это означает, что особям известна лишь численность той субпопуляции, которой они принадлежат на данном шаге времени t, и те условия окружающей среды (выраженные параметрами a и b либо c и d соответственно), в которых они существует в данный момент времени, и цена перемещения p. В отсутствии миграции динамика популяции в каждой из стаций описывается уравнением (1).
В случае локальной информированности особи при выборе способа пространственного поведения – мигрировать или оставаться – опираются лишь на ту информацию, которая касается их стации пребывания. Понятно, что конкретный выбор такого рода информации существенно зависит от деталей структуры рассматриваемого биологического сообщества. Тем не менее весьма разумным с биологической точки зрения является механизм, в котором миграции носят пороговый характер: особи эмигрируют, когда плотность популяции (либо численность в рамках нашей модели) превышает некоторую критическую величину N* (M* соответственно).
Напомним, что модели, рассматриваемые в настоящей работе, строятся в одношаговом приближении оптимизации среднего по пространству КР: максимизируется его значение в следующем поколении. Здесь становится естественным следующий подход к выбору критических значений N* и M*: эмиграция на шаге времени t начинается тогда, когда численность
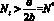 и
и 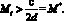 (5)
(5)
Такой выбор (5) величины критической численности означает, что миграция начинается тогда, когда в силу динамики складывается численность, при которой число потомков в следующем поколении будет меньше, чем в текущем, из-за внутрипопуляционных эффектов, связанных с перенаселением. Предполагается, что при превышении критического значения численности в какой-либо из стаций случайным образом выбираются мигранты, и та доля субпопуляции, которая превышает оптимальную численность, эмигрирует.
Опишем ещё раз кратко работу данной модели. На каждом шаге времени t текущие численности Nt и Mt сравниваются со значениями оптимальных численностей N* и M*. Затем, если требуется, происходит акт миграции; особо подчеркнём, что решение о миграции принимается особями каждой из субпопуляций независимо. Это приводит к тому, что численность может измениться (хотя бы в одной стации) и перестать быть оптимальной. Затем происходит размножение в силу уравнений (1) с изменёнными численностями 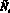 и
и 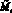 :
:
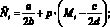
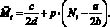 (6)
(6)
Численные эксперименты
Для сравнения динамики численностей глобально и локально информированных особей были проведены численные эксперименты. Проводилось сканирование области параметров для следующих значений: a и c изменялись от 2 до 10 с шагом 0,16, b и d изменялись от 0,0001 до 0,001 с шагом 0,000018, p изменялось от 0,1 до 1 с шагом 0,1. То есть для каждого параметра, кроме p, делалось 50 шагов в интервале его изменения. Для каждого набора параметров количество шагов по времени равнялось 1000 и начальные численности в каждой из стаций равнялись 1000 особей.
Для каждого значения цены перемещения p перебирались 504 наборов параметров a, b, c, d и вычислялись суммарные средние численности по обеим стациям за 1000 шагов по времени. Вычислялись следующие суммарные численности: N – средняя суммарная численность по двум стациям для модели глобально информированных особей, L – средняя суммарная численность по двум стациям для модели локально информированных особей. Исходя из значений N и L для каждого значения p вычислялись следующие показатели: SN – количество наборов параметров, при которых N > L, SL – количество наборов параметров, для которых L > N и SRavn – количество наборов параметров, для которых N = L. Таким образом, мы выясняли, какой тип информированности особей дает им преимущество по численности для каждого набора параметров. В таблице показано процентное соотношение SN, SL и SRavn к общему количеству наборов параметров (105 наборов) для каждого значения.
|
p |
SN, % |
SL, % |
SRavn, % |
|
0,1 |
0 |
96 |
4 |
|
0,2 |
0 |
96 |
4 |
|
0,3 |
0 |
96 |
4 |
|
0,4 |
0 |
95,84 |
4,16 |
|
0,5 |
0 |
95,2 |
4,8 |
|
0,6 |
0 |
94,4 |
5,6 |
|
0,7 |
0,96 |
93,6 |
5,44 |
|
0,8 |
1,92 |
92 |
6,08 |
|
0,9 |
5,12 |
88,32 |
6,56 |
|
1 |
6, 17 |
86,55 |
7,28 |
Как видно из таблицы, для всех значений параметра p локальная информированность дает преимущество по средним численностям в подавляющем большинстве случаев. Это объясняется тем, что при небольших значениях параметра p миграция в модели локальной информированности является «стоком» для «излишков» особей и позволяет поддерживать в стациях численности, близкие к максимальным. Равенство средних численностей N и L наблюдалось в тех случаях, когда миграции между стациями отсутствовали в обеих моделях, то есть для значений параметров a < 3, c < 3. Модель глобально информированных особей давала преимущество по средним численностям в тех случаях, когда наблюдались встречные миграции локально информированных особей при больших значениях параметра p. При этом не происходило резкой убыли численности в стациях, заложенной в цене перемещения, и на следующем шаге по времени наблюдалось уменьшение численности, поскольку были превышены оптимальные численности.
Рецензенты:
Заворуев В.В., д.б.н., ведущий научный сотрудник, Институт вычислительного моделирования СО РАН, г. Красноярск;
Садовский М.Г., д.ф.-м.н., ведущий научный сотрудник, Институт вычислительного моделирования СО РАН, г. Красноярск.



