Задачи, связанные с исследованиями атмосферных электростатических полей, содержат одно из граничных условий, задаваемое на бесконечности, поэтому они относятся к внешним краевым задачам [1, 16]. Для расчетов систем молниезащит (СМЗ) стартовых площадок разработано достаточно много подходов. В [12] представлены обзор СМЗ стартовых площадок и возможные подходы к моделированию процессов, например как в [5, 6]. В [13] исследованы особенности СМЗ одного из индийских стартовых комплексов.
Среди существующих нелинейных математических моделей, предназначенных для исследования процессов образования и встречного движения нисходящего лидера молнии и восходящего лидерного разряда, необходимо отметить разработанные модели Ericsson [10], Dellera и Garbagnati [8, 9], Rizk [17], Becerra и Cooray [4]. В [8] показан пример исследования опор линий электропередач с учетом рельефа местности, причем в виде расчетов каналов разряда, представленных некоторым семейством линий в пространстве от грозового облака до объектов на поверхности земли, но без учета их разветвления. Наряду с этими моделями широко используются упрощенные методики, методы и различные эмпирические зависимости. Например, анализ основных их них дан в [7] с учетом их особенностей, а также отмечено, что среди существующих методов проектирования СМЗ нет количественного подхода и отмечены недостатки анализируемых методик и методов.
Цель работы связана:
1) с развитием метода расчета электростатических полей для исследуемого распределенного объекта ?0 в виде молниеприемников СМЗ и ракеты-носителя на основе вычисления удельного распределения линий функции потока (ЛФП), т.е. силовых линий электростатического поля в расчетной области при проведении вычислительных экспериментов;
2) с выявлением на базе результатов расчета возможных оценочных критериев определения эффективности перехвата молний исследуемыми схемами внешних СМЗ.
Постановка задачи
За основу принята схема расчетной области на базе типовой стартовой площадки космодрома с учетом обзора [12]. Исходная схема в плане имеет вид квадрата или прямоугольника, по углам которого находятся пирамидальные башни с размещенными на их вершинах цилиндрическими стержнями (считается, что стержни являются металлическими, но в [2] в рамках расчета потенциальных полей исследуется возможность их представления в виде изоляторов). Конструкция молниеприемника в целом считается цилиндрической. В [15] на примере расчета трехмерной задачи показано, что внешняя краевая задача с минимальными погрешностями сводится к внутренней. Это распространяется на ?0, находящийся в центральной части области D(x, y) относительно 2-х горизонтальных плоскостей, а именно нижней части облака V(x, y) и поверхности земли F(x, y).
Схема на рис. 1 представлена в вертикальной плоскости, проходящей через элементы 1, 4 (молниеприемники внешней СМЗ) и 5 (ракета-носитель или технологическая мачта) [1, 16].
Считается, что ?0 включает элементы 1, 4 и 5, причем они представляются в виде линий (определяется соотношениями их размеров высоты и боковых габаритов). Границы области D(x, y) следующие: G1 – граница в виде поверхности земли F(x, y); G2 – нижняя граница облака V(x, y); G3, G4 – границы для искусственного ограничения области D(x, y) путём введения в постановку задачи граничного условия Еn = 0 (Еn – напряжённость электростатического поля по нормали к G3, G4) [1,16]. Следует заметить, что в этой задаче не учитывается краевой эффект от V(x, y), как в [15]. Обозначения дистанций на схеме следующие: l1 – расстояние между молниеприемником 1 и объектом защиты 5; l2 – расстояние между 5 и одной из боковых границ D(x, y).
Задача решается в два этапа [1, 16]. На первом этапе используется уравнение Лапласа для определения электростатического поля в расчетной области D(x,y). Схема области D(x,y) относительно приближена к реальным соотношениям размеров между нижней границей облака V(x, y) и поверхностью F(x, y) с учетом ?0. Этот этап необходим для масштабирования исследуемого ?0 в области D(x, y) с корректным переходом к новой области D1(x,y) на основе применения модифицированной методики [3] на базе ортогональной сетки семейства эквипотенциальных линий в виде уравнений ?i(x, y) = const и ЛФП в виде уравнений µi(x, y) = const, например, как показано в [1, 16].
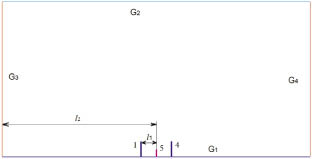
Рис. 1. Схема расчетной области D(x,y) с ?0 в виде элементов 1, 4 (молниеприемники) и 5 (ракета-носитель или технологическая мачта)
1. Первый этап. В области D(x, y) из уравнения Лапласа с учетом граничных условий (рис. 1) определяются поле потенциала ? и семейства ?i(x, y) = const и µi(x, y) = const [16].
Допущения следующие. Считаем, что V(x, y) – исходное грозовое облако. Полагаем, что на G2 потенциал равен ?01 и исследуется электростатическое поле. Считается, что это поле относительно мало, т.е. подход справедлив до начала коронного разряда в грозовых облаках и при отсутствии объёмных электрических зарядов в атмосфере области D(x, y).
В результате расчетов определяется область D1(x, y) [1, 16] (рис. 2), особенность ее в том, что вместо границы G2 появляется G22, (эквипотенциальная линия 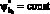 из семейства ?i(x,y) = const на заданной высоте с учетом применения модифицированной методики [3]). Обозначения границ, как и на рис. 1, но с дополнительным индексом 1.
из семейства ?i(x,y) = const на заданной высоте с учетом применения модифицированной методики [3]). Обозначения границ, как и на рис. 1, но с дополнительным индексом 1.

Рис. 2. Схема масштабированной области D1(x,y) (цифровые обозначения, как на рис. 1)
2. Второй этап. Схема масштабированной области D1(x,y) показана на рис. 2 с учетом симметрии относительно 5, тогда ?0 включает элементы 1 и 5. Поле функции потока µi определяется из уравнения эллиптического типа (1), аналогичного уравнению Лапласа с учетом того, что граничные условия для функций µ и ? различаются:
?2µ/?x2 + ?2µ/?y2 = 0; (x,y) ? D1(x,y). (1)
Граничные условия задачи c учётом рис. 2 следующие:
? на границе G21:
?µ/?n = 0; (x,y) ? G21; (2)
? на границах G11 (молниеприемник 1) и G15 (объект защиты 5):
?µ/?n = 0; (x,y) ? G11, G15; (3)
? на границе G31:
µ(x,y) = µ01; (x,y) ? G31; (4)
? на границе G41:
µ(x,y) = 0; (x,y) ? G41; (5)
? на границе G22:
µ(x,y) = 0; (x,y) ? G22; (6)
где D1(x, y) – исследуемая область и ограничена G21, G22, G31, G41, G11, G15.
Для оценки и сравнительного анализа особенностей элементов объекта ?0 вводится дополнительная граница G23 на краю границы G22. Считаем, что ЛФП (в виде семейства µi(x,y) = const) начинаются с G23. Тогда на ней записывается условие вида
?µ/?n = 0; (x,y) ? G23. (7)
Следовательно, на оставшейся части границы G22 выполняется условие (6).
Результаты расчетов и сравнительный анализ
Для краевой задачи с учетом математической модели в виде уравнения эллиптического типа (1) с граничными условиями (2)–(7), с использованием итерационного метода верхней релаксации и на базе программных средств, выполним вычислительные эксперименты для определения удельного распределения ЛФП относительно ?0 в масштабированной D1(x, y). Расчет уединенного стержневого молниеприемника в трехмерной области с использованием итерационного метода верхней релаксаций дан, например, в [15].
Результаты расчетов представляются в безразмерном виде:
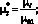
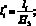
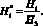 (8)
(8)
Приняты нормирующие значения: для функции потока – µ01; для дистанций и высот в области D1(x, y) – H3 (высота объекта защиты 5). Остальные величины нормируются аналогичным образом.
Результаты расчета первого этапа даны в [1, 16]. Следует отметить, что высота от F(x, y) до V(x, y) в исходной области D(x, y) принималась 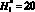 . Например, в абсолютных величинах при H3 = 50 м, тогда высота H1 = 1000 м и расстояние l2 = 1000 м. В области D1(x, y) с учетом ?0 (рис. 2) принимаются следующие условия: дистанция
. Например, в абсолютных величинах при H3 = 50 м, тогда высота H1 = 1000 м и расстояние l2 = 1000 м. В области D1(x, y) с учетом ?0 (рис. 2) принимаются следующие условия: дистанция 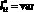 . Высота объекта защиты
. Высота объекта защиты 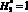 , относительная высота
, относительная высота 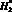 молниеприемника СМЗ принимается в виде 2-х значений
молниеприемника СМЗ принимается в виде 2-х значений 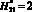 или
или 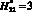 . Высота
. Высота 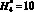 до некоторой эквипотенциальной линии
до некоторой эквипотенциальной линии 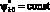 (введенной вместо границы G2, т.е. V(x, y) в условиях перехода от области D(x,y) к масштабированной D1(x,y)).
(введенной вместо границы G2, т.е. V(x, y) в условиях перехода от области D(x,y) к масштабированной D1(x,y)).
При вычислительных экспериментах в условиях изменения независимых переменных  с шагом
с шагом 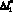 и
и 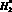 определяется следующее:
определяется следующее:
1) количество ni ЛФП в виде некоторого семейства µi(х, у) = const в области D1(x, y);
2) удельное распределение ЛФП относительно элементов ?0 в D1(x, y).
Типичный пример результатов расчета ЛФП для 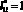 и при
и при 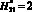 с условием ni = var показан на рис. 3. За основу для последующих расчетов приняты результаты (рис. 3) при ni1 = 100. Результаты вычислительного эксперимента, полученные с учетом
с условием ni = var показан на рис. 3. За основу для последующих расчетов приняты результаты (рис. 3) при ni1 = 100. Результаты вычислительного эксперимента, полученные с учетом 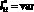 и при
и при 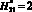 , сведены в табл. 1.
, сведены в табл. 1.
Введены следующие обозначения:
1) ?1i – величина удельного распределения ЛФП объекта защиты 5 (соответственно часть ?0) также представляется как функция 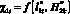 ;
;
2) ?2i – величина удельного распределения ЛФП по F(x, y) также представляется как 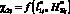 ;
;
3) ?3i – величина удельного распределения ЛФП молниеприемника СМЗ (соответственно часть ?0), также представляется как 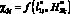 .
.
На основе результатов табл. 1 представим особенности характеристик ?i прежде всего для элементов ?0 в виде 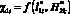 и
и 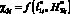 (рис. 4), а также для F(x, y) в виде
(рис. 4), а также для F(x, y) в виде 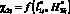 (рис. 5). Эти характеристики показаны в дискретном виде с учетом выполнения закона электростатики.
(рис. 5). Эти характеристики показаны в дискретном виде с учетом выполнения закона электростатики.
Таблица 1
Удельное распределение ЛФП ?i в области D1(x, y) при 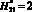 и
и 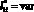
|
?i – величина исследуемого элемента в D1(x, y) |
Дистанция |
||||||||
|
0,8 |
1,2 |
1,6 |
2,0 |
2,4 |
2,8 |
3,2 |
3,6 |
4,0 |
|
|
?1i |
0,030 |
0,060 |
0,090 |
0,120 |
0,145 |
0,165 |
0,180 |
0,195 |
0,200 |
|
?2i |
0,300 |
0,230 |
0,175 |
0,150 |
0,145 |
0,175 |
0,220 |
0,285 |
0,380 |
|
?3i |
0,670 |
0,710 |
0,735 |
0,730 |
0,710 |
0,660 |
0,600 |
0,52 |
0,420 |



a б в
Рис. 3. Результаты расчета семейства µi(х,у) = const для 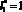 и
и 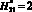 : при ni1 = 100 (a), ni2 = 30 (б) и ni3 = 20 (в)
: при ni1 = 100 (a), ni2 = 30 (б) и ni3 = 20 (в)
Из анализа характеристики на рис. 4, а следует, что изменение функции вида 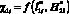 нелинейное, причем минимальное значение ?1min = 0,03 при
нелинейное, причем минимальное значение ?1min = 0,03 при 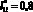 . Тогда как другие функции в области D1(x, y), а именно,
. Тогда как другие функции в области D1(x, y), а именно, 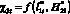 (рис. 4, б) и
(рис. 4, б) и 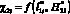 (рис. 5) при этих же условиях имеют значительно большие значения в сравнении с
(рис. 5) при этих же условиях имеют значительно большие значения в сравнении с 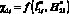 при
при 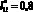 , например, ?3i > ?1i (более чем в 20 раз). Учитывая, что
, например, ?3i > ?1i (более чем в 20 раз). Учитывая, что 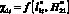 применяется для оценки объекта защиты на основе удельного распределения ЛФП в D1(x, y), а
применяется для оценки объекта защиты на основе удельного распределения ЛФП в D1(x, y), а 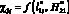 – для оценки стержневого молниеприемника, тогда на базе полученных результатов имеется возможность установить оценочный критерий определения эффективности перехвата молний для различных схем СМЗ стартовых площадок в следующем виде.
– для оценки стержневого молниеприемника, тогда на базе полученных результатов имеется возможность установить оценочный критерий определения эффективности перехвата молний для различных схем СМЗ стартовых площадок в следующем виде.
Чем больше величина удельного распределения ЛФП на молниеприемниках СМЗ и чем она существенно меньше на объектах защиты, тем выше эффективность перехвата молний для исследуемых схем на основе распределенных стержневых молниеприемников СМЗ для ракет-носителей.
По-видимому, для дальнейшего уменьшения  существуют ограничения, как по конструктивным параметрам внешних СМЗ (например, в виде пирамидальных башен с размерами в нижней их части большими, чем в верхней), так и по другим, например по физическим параметрам при ударах молний.
существуют ограничения, как по конструктивным параметрам внешних СМЗ (например, в виде пирамидальных башен с размерами в нижней их части большими, чем в верхней), так и по другим, например по физическим параметрам при ударах молний.
Рассмотрим особенности ?0 в условиях увеличения высоты 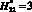 , т.е. в 1,5 раза по сравнению с
, т.е. в 1,5 раза по сравнению с 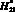 . Например, в абсолютных величинах H21 = 100 м, а H22 = 150 м (т.е. это высоты 2-х молниеприемников на космодроме Восточный). Результаты вычислительных экспериментов при
. Например, в абсолютных величинах H21 = 100 м, а H22 = 150 м (т.е. это высоты 2-х молниеприемников на космодроме Восточный). Результаты вычислительных экспериментов при 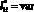 и
и 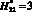 сведены в табл. 2.
сведены в табл. 2.
Из анализа табл. 2 следует, что величина ?1min существует при 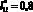 , причем она уменьшилась в 10 раз по сравнению с данными при
, причем она уменьшилась в 10 раз по сравнению с данными при 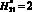 (практически равна нулю). Важно отметить, что функция
(практически равна нулю). Важно отметить, что функция 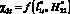 при
при 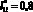 (табл. 2) имеет существенно большее значение в сравнении с
(табл. 2) имеет существенно большее значение в сравнении с 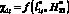 , а также имеет максимум при
, а также имеет максимум при 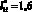 .
.
a б
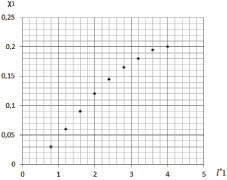
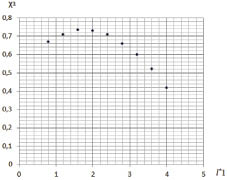
Рис. 4. Результаты расчета удельного распределения ЛФП при 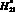 и
и 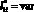 (ni1 = 100): величина ?1 объекта защиты (a) и величина ?3 молниеприемника СМЗ (б)
(ni1 = 100): величина ?1 объекта защиты (a) и величина ?3 молниеприемника СМЗ (б)
Таблица 2
Удельное распределение ЛФП ?i в области D1(x, y) при 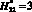 и
и 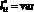 (без учета ?2i)
(без учета ?2i)
|
?i – величина исследуемого элемента в D1(x, y) |
Дистанция |
|||||||
|
0,8 |
1,2 |
1,6 |
2,0 |
2,4 |
2,8 |
3,2 |
3,6 |
|
|
?1i |
0,003 |
0,015 |
0,045 |
0,065 |
0,085 |
0,095 |
0,115 |
0,125 |
|
?3i |
0,829 |
0,865 |
0,870 |
0,860 |
0,835 |
0,805 |
0,740 |
0,655 |
С учетом оценочного критерия определения эффективности перехвата молний внешними СМЗ этот результат показывает следующее. Если для функции 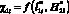 существует некоторая величина ?1min = 0,03 при
существует некоторая величина ?1min = 0,03 при 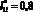 , то тогда для функции
, то тогда для функции 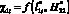 , т.е. при
, т.е. при 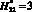 , величина ?1min = 0,03 будет находиться на дистанции в пределах до
, величина ?1min = 0,03 будет находиться на дистанции в пределах до 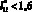 (табл. 2). Следовательно, при увеличении высоты молниеприемника в 1,5 раза можно изменить дистанцию
(табл. 2). Следовательно, при увеличении высоты молниеприемника в 1,5 раза можно изменить дистанцию  в пределах до 2-х раз при ?1min = const. Это важно в условиях оптимизации параметров молниеприемников СМЗ относительно ракеты-носителя.
в пределах до 2-х раз при ?1min = const. Это важно в условиях оптимизации параметров молниеприемников СМЗ относительно ракеты-носителя.
В целом анализ данных на рис. 4, б показывает, что изменение функции 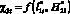 (для молниеприемника СМЗ) является нелинейным и представляется в виде некоторой параболической зависимости, причем с максимумом на дистанции
(для молниеприемника СМЗ) является нелинейным и представляется в виде некоторой параболической зависимости, причем с максимумом на дистанции 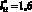 . Также из полученных данных следует, что при экстремуме функции
. Также из полученных данных следует, что при экстремуме функции 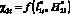 , тогда на объекте защиты ?1 = 0,09, т.е. больше, чем ?1min. Вывод следующий: максимум функции
, тогда на объекте защиты ?1 = 0,09, т.е. больше, чем ?1min. Вывод следующий: максимум функции 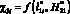 молниеприемника и минимальное значение
молниеприемника и минимальное значение 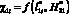 объекта защиты не совпадают. Это связано с тем, что происходит перераспределение исследуемых функций
объекта защиты не совпадают. Это связано с тем, что происходит перераспределение исследуемых функций 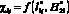 в расчетной области с учетом F(x, y). Аналогично это наблюдается и при изменениях высоты молниеприемника (данные табл. 2).
в расчетной области с учетом F(x, y). Аналогично это наблюдается и при изменениях высоты молниеприемника (данные табл. 2).
Сопоставительный анализ показывает, что представленный подход отличается от нелинейных математических моделей, так как вычислительные эксперименты проводятся в рамках электростатических полей. Однако это дает возможность получать количественные результаты для исследуемых ?0 в сравнении с упрощенными подходами, анализ которым дан, например, в [7].
В качестве примера для сравнительного анализа полученных результатов с существующими данными рассмотрим схему стержневых молниеприемников СМЗ для баллистических ракет, применяемую на одном из полигонов США. В этой системе старта ракеты применяются стержневые молниеприемники, устанавливаемые на минимальных дистанциях (в пределах 2–3-х де сятков метров от корпуса ракеты), в связи с применением цилиндрической формы молниеприемников [11]. В сравнении с данными [12, 13] эти дистанции на порядок меньше. Это определяется особенностями конструкций стержневых молниеприемников, например на стартовых площадках ракет-носителей с космическими аппаратами применяются составные молниеприемники [12, 13] в виде решетчатых конструкций пирамидального типа с соответствующими габаритами в нижней части. Данные [11] с минимальными дистанциями от стержневых молниеприемников до корпуса ракеты косвенно подтверждают полученные результаты на основе вычислительных экспериментов для стержневых молниеприемников СМЗ стартовых площадок. А именно ? при уменьшении дистанции  функция
функция 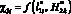 молниеприемника стремится к некоторому относительно максимальному значению, тогда как определяемая функция
молниеприемника стремится к некоторому относительно максимальному значению, тогда как определяемая функция 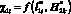 объекта защиты стремится к минимуму.
объекта защиты стремится к минимуму.
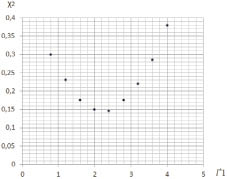
Рис. 5. Результаты расчета удельного распределения ЛФП при 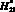 и
и 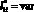 (ni1 = 100) для F(x, y)
(ni1 = 100) для F(x, y)
По-видимому, расчеты на основе 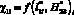 и
и 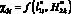 могут применяться при анализе и выборе рациональных технических решений для СМЗ стартовых площадок. В целом возможно при проектировании внешних схем СМЗ определять величины ?3i, а расчеты на основе величин ?1i необходимо использовать в виде проверочных.
могут применяться при анализе и выборе рациональных технических решений для СМЗ стартовых площадок. В целом возможно при проектировании внешних схем СМЗ определять величины ?3i, а расчеты на основе величин ?1i необходимо использовать в виде проверочных.
Анализ характеристики (рис. 5) показывает, что изменение функции 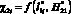 также имеет вид некоторой параболической зависимости, но с минимумом при
также имеет вид некоторой параболической зависимости, но с минимумом при 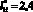 . Следует заметить, что функция
. Следует заметить, что функция 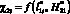 представляет удельное распределение ЛФП по F(x, y), на которой они расположены, поэтому ?2i не представляет важности для исследуемого распределенного объекта ?0. Однако эта функция может применяться для возможного обоснования существования экспериментальных эффектов, связанных с ударами молний не только в вершины объектов, но и в боковые их части, а также в поверхность F(x, y), на которой они расположены.
представляет удельное распределение ЛФП по F(x, y), на которой они расположены, поэтому ?2i не представляет важности для исследуемого распределенного объекта ?0. Однако эта функция может применяться для возможного обоснования существования экспериментальных эффектов, связанных с ударами молний не только в вершины объектов, но и в боковые их части, а также в поверхность F(x, y), на которой они расположены.
Например, такой эффект был зафиксирован на космодроме в США, а именно в виде удара молнии в нижнюю часть стартовой площадки с шаттлом [14], причём в условиях применения стержневого молниеприемника СМЗ с высотой, существенно превышающей высоту шаттла на этом космодроме.
Выводы
1. Установлено, что имеется возможность в рамках развиваемой математической модели выполнять сравнительный анализ схем технических решений в виде стержневых молниеприемников СМЗ на основе количественного анализа удельного распределения ЛФП для исследуемых объектов, находящихся в атмосферном электростатическом поле в условиях отсутствия коронных разрядов и объёмных электрических зарядов в расчетной области. Сформулирован оценочный критерий определения эффективности перехвата молний для исследуемых схем СМЗ стартовых площадок.
2. При вычислительных экспериментах показано, что величины удельного распределения ЛФП на объекте защиты и молниеприемнике СМЗ в виде функций 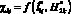 , при условии
, при условии 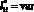 (от объекта защиты до молниеприемника) являются нелинейными, причем их экстремумы не совпадают.
(от объекта защиты до молниеприемника) являются нелинейными, причем их экстремумы не совпадают.
3. Выявлено, что существует возможность оптимизировать соотношения функций удельного распределения ЛФП на объекте защиты и молниеприемнике СМЗ при изменениях величин  ,
, 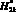 , а также иных, в связи с этим имеется возможность выбора рациональных технических решений для внешних СМЗ стартовых площадок.
, а также иных, в связи с этим имеется возможность выбора рациональных технических решений для внешних СМЗ стартовых площадок.
Рецензенты:
Уваров В.А., д.т.н., профессор, директор АСИ, ФГБОУ «Белгородский государственный технологический университет им. В.Г. Шухова», г. Белгород;
Логачев К.И., д.т.н., профессор кафедры ТГиВ, «Белгородский государственный технологический университет им. В.Г. Шухова», г. Белгород.




 до молниеприемника СМЗ
до молниеприемника СМЗ до элемента внешней СМЗ
до элемента внешней СМЗ