При синтезе систем управления манипуляционными роботами (МР) требуется решать задачи кинематики. Различаются прямая и обратная задачи кинематики (ОЗК). Прямая задача кинематики состоит в определении пространственного положения и ориентации характерной точки (схвата МР) по известным значениям обобщенных координат. Обратная задача кинематики робота-манипулятора заключается в определении обобщенных координат (ОК) МР по известному угловому и линейному местоположению схвата манипулятора. Прямая задача решается однозначно, в то время как ОЗК, представляющая собой противоположную задачу, как правило, не имеет единственного решения [3?5].
Формулировка ОЗК
По заданному (6?1) вектору линейных координат положения и угловых координат ориентации схвата МР
Sc = (xc, yc, zc, ?c, ?c, ?c)T
вычисляется (n?1) вектор обобщенных координат звеньев
q = (q1, q2, ..., qn)T,
где xc, yc, zc – пространственные координаты положения схвата МР; ?c, ?c, ?c – угловые координаты ориентации схвата МР, qi, i = 1...n – обобщенные координаты звеньев МР [1].
Методы решения ОЗК для МР можно разделить на точные (аналитические) и приближенные (итерационные). В результате использования точных методов вектор ОК удается получить в виде аналитической зависимости геометрических параметров кинематической схемы МР. В этом случае процесс нахождения искомого вектора ОК по вектору положения и ориентации схвата МР при известной кинематической схеме сводится к вычислению значений заранее полученных аналитических зависимостей. Но точное решение удается получить не для любой кинематической схемы манипулятора.
Приближенные методы – это методы численного решения уравнений связи. Они оказываются работоспособными для любых кинематических схем. Однако это связано с использованием рекуррентных процедур. Среди них можно выделить группу методов, основанных на использовании матрицы Якоби: метод Ньютона, метод Гаусса – Ньютона, метод Левенберга – Марквардта [1].
Метод штрафных функций для решения ОЗК
В статье развивается новый метод решения обратных задач кинематики роботов-манипуляторов, основанный на использовании метода штрафных функций. Метод штрафных функций относятся к группе непрямых методов решения задач нелинейного программирования [2].
Рассмотрим методику применения метода штрафных функций на примере нахождения ОК для трехзвенного планарного манипулятора.
Координаты положения схвата МР (xc, yc) для приведенной конфигурации (рис. 1) определяются из соотношений
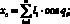
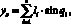 (1)
(1)
где li, i = 1...3 – длины звеньев МР.
Рассмотрим критерий
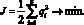 (2)
(2)
Введем расширенный критерий
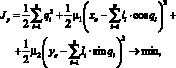 (3)
(3)
где ?1, ?2 – весовые коэффициенты.
Для минимизации расширенного критерия воспользуемся методом градиента. Для этого вычислим частные производные по обобщенным координатам:
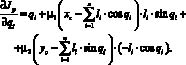 (4)
(4)
Таким образом, значения обобщенных координат определятся из соотношения
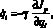 (5)
(5)
где ? > 0 – коэффициент, определяющий скорость настройки.
Приведенный алгоритм реализован в среде Matlab. При проведении численных экспериментов рассматривались два варианта движения МР:
– выход схвата в точку с заданными координатами (xc, yc) = (0,24 м; 0,12 м). На рис. 2 приведены решения дифференциальных уравнений (5) при различных значениях весовых коэффициентов ?1, ?2. Также приведены величины отклонений между установившимся и желаемым положением характерной точки МР ex = xуст – xc, ey = yуст – yc;
– движение схвата МР по заданной программной траектории
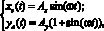
где Ax = 0,12 м, Ay = 0,24 м, w = 0,75 рад/с.
На рис. 3 приведены программные траектории движения схвата МР при различных значениях весовых коэффициентов ?1, ?2. Также приведены величины максимальных отклонений при движении по программной траектории exmax, eymax.
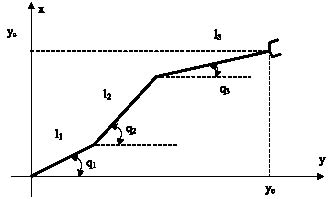
Рис. 1. Трехзвенный манипулятор
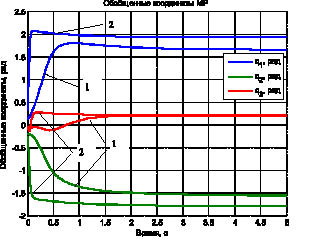
а
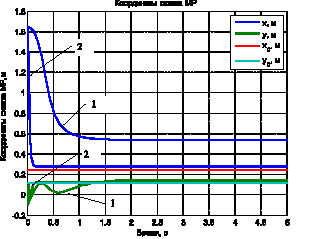
б
Рис. 2. Обобщенные координаты МР (а), координаты схвата МР (б). Моделирование при 1 – ?1 = ?2 = 1. Расхождение ex = 0,2995 м, ey = 0,0264 м; 2 – ?1 = ?2 = 10. Расхождение ex = 0,0360 м, ey = 0,0038 м
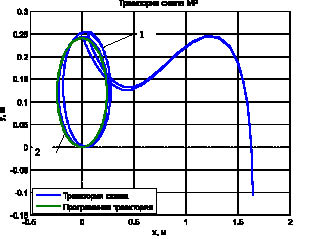
Рис. 3. Программная траектория движения схвата МР. 1 – моделирование при ?1 = ?2 = 5. Расхождение exmax = 0,114 м, eymax = 0,0023 м. 2 – моделирование при ?1 = ?2 = 50. Расхождение exmax = 0,0135 м, eymax = 0,003 м
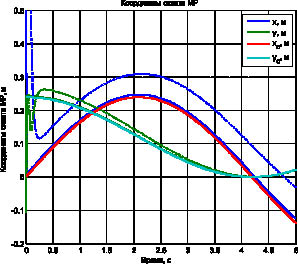
Рис. 4. Координаты схвата МР. 1 – моделирование при ?1 = ?2 = 5 (штрихпунктирные линии). 2 – моделирование при ?1 = ?2 = 50 (сплошные линии)
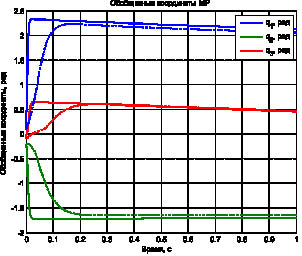
Рис. 5. Обобщенные координаты схвата МР. 1 – моделирование при ?1 = ?2 = 5 (штрихпунктирные линии). 2 – моделирование при ?1 = ?2 = 50 (сплошные линии)
На рис. 4, 5 приведены графики, показывающие переходные процессы координат схвата и обобщенных координат МР.
Как видно из приведенных графиков, с течением времени происходит стабилизация решений дифференциальных уравнений и их стремление к установившимся значениям за конечное время. Также необходимо отметить, что увеличение значений весовых коэффициентов ?1, ?2 приводит к ускорению схождения решения.
Заключение
В результате численного решения дифференциальных уравнений для любых начальных значений обобщенных координат МР из их рабочих диапазонов его обобщенные координаты примут в конечный момент времени значения, соответствующие требуемому положению схвата МР, и, следовательно, приведут к решению ОЗК.
Достоинства используемого метода заключаются в единственности решения для заданной кинематической схемы МР и начального состояния манипулятора, высокой точности решения и быст родействия.
Работа поддержана Министерством науки и образования Российской Федерации, Государственный контракт 02G25.31.0025.
Рецензенты:
Завьялов В.В., д.т.н., профессор ка федры технических средств судовождения, Морской государственный университет имени адмирала Г.И. Невельского, г. Владивосток;
Верёвкин В.Ф., д.т.н., профессор кафедры электрооборудования и автоматики судов, Морской государственный университет имени адмирала Г.И. Невельского, г. Владивосток.



