Исследование безопасности в техносфере тесно связано с изучением случайных процессов. Наиболее адекватным методом их описания является применение дискретных по значению и непрерывных во времени случайных процессов, моделирующих потоки событий, формирующих предпосылки и условия возникновения опасных проявлений техносферы. По аналогии с цифровой техникой при таком подходе момент перехода некоторой случайной функции времени от низкого уровня к высокому будет соответствовать моменту возникновения события, длительность этого состояния – длительности существования события, переход от высокого уровня к низкому – моменту его устранения.
В силу сложности вопросов безопасности в качестве инструмента исследования целесообразно применить имитационное моделирование. В общем случае имитационная модель – это логико-математическое описание объекта, которое может быть использовано для экспериментирования на компьютере в целях проектирования, анализа и оценки функционирования объекта. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться совокупностью процессов, имеющих случайный характер. По этим данным можно получить достаточно устойчивую статистику.
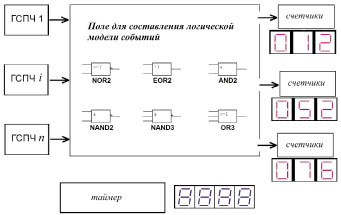
В анализе безопасности достаточно распространены методы, основанные на применении графических структур типа деревьев событий (неисправностей и т.п.) [5]. Принципиально общим у этого направления является использование логических функций булевой алгебры (И, ИЛИ, И-НЕ, ИЛИ-НЕ исключающее ИЛИ), которые легко реализуются в программах схемотехнического моделирования.
Для имитационного моделирования авторы предлагают использовать аналого-цифровые электронные схемы, созданные в среде Multisim. Простота и наглядность процедуры изменения структуры дерева событий путем устранения или добавления логических элементов в программе «Multisim» обеспечивает эффективность предлагаемой структуры имитационной модели. Аналогично можно использовать и MicroCAP, Labview и другие программные продукты, предназначенные для схемотехнического моделирования.
В качестве модели источника случайных событий предлагается использовать генератор псевдослучайных чисел, отличительной особенностью которого является большая средняя частота появления сигналов – в зависимости от решаемой задачи её можно выбрать в диапазоне десятков-сотен мегагерц. В итоге реальные события, возникающие в интервалах тысяч – миллионов часов моделируются за доли секунды. На практике степень сжатия во времени определяется быстродействием компьютера и сложностью цифровой логической схемы, моделирующей структуры деревьев событий, описывающих различные сценарии возникновения угроз безопасности
Как отмечалось выше, в анализе безопасности широко применяются бинарные состояния типа «исправен-неисправен». Случайные процессы с «качественными» состояниями относятся к категории марковских процессов с непрерывным временем и дискретными состояниями. Понятие «состояние» является качественным и позволяет анализировать самые различные физические процессы. Неотъемлемой частью описания состояния дискретного случайного процесса является понятие «события», под которым будем понимать любой переход из одного состояния в другое. При анализе безопасности событиями являются не только факт возникновения угроз безопасности, но и факт их устранения, поэтому существенно важным является длительность нахождения в этом угрожающем состоянии. Таким образом, имеем два качественных состояния – «0» и «1», соответствующие соответственно состояниям «исправен» и «неисправен». Данный простейший случай двух состояний рассмотрен в [1], где приведены следующие формулы:
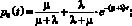
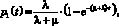
где ? – интенсивность отказов (переход из состояния 0 в состояние 1); ? – интенсивность восстановления (переход из состояния 1 в состояние 0).
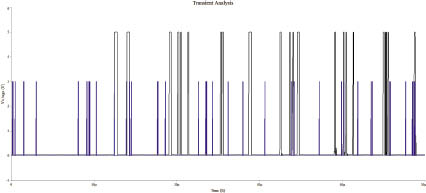
Рассматриваемый поток событий получаем после пороговой обработки случайного процесса, имитируемого генератором теплового шума, схема которого приведена на рис. 1.
Значение интенсивности потока событий задается уровнем порога их обнаружения и определяется количеством пересечений заданного порога за время наблюдения. Таким образом, в предлагаемой модели объединяются два подхода к исследованию случайных процессов в сфере безопасности: на основе теории марковских процессов и с применением логических моделей, описывающих причинно-следственные связи между событиями, формирующими угрозы безопасности.
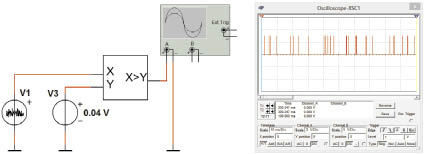
Рис. 1. Схема задающего генератора случайного потока импульсов и генерируемый им поток событий
Важнейшей задачей при реализации аналого-цифровой модели случайных процессов является получение нескольких – в общем случае n – статистически независимых источников потоков случайных событий, то есть случайных последовательностей. Как известно, для получения настоящих случайных последовательностей используют физические источники энтропии – например флуктуации тока в резисторе (тепловой шум), дробовой шум в электронно-вакуумных приборах, детекторы событий ионизирующей радиации или космического излучения и т.п. [2, 4]. В криптографии псевдослучайная цифровая последовательность чаще всего формируется последовательными регистрами сдвига с линейной обратной связью (РСЛОС). Для получения сигнала обратной связи используется элемент «исключающее ИЛИ», реализующий операцию XOR над некоторыми битами регистра, определяемыми последовательностью отводов обратной связи [3, 4]. Этот алгоритм имеет большую скорость работы и генерирует последовательности, статистически неотличимые от случайных. Однако любой генератор псевдослучайных чисел (ГПСЧ) с ограниченными ресурсами рано или поздно зацикливается – начинает повторять одну и ту же последовательность чисел. Если порождаемая последовательность ГПСЧ сходится к слишком коротким циклам, то такой ГПСЧ становится предсказуемым и непригодным для практических приложений.
Линейные кодовые последовательности имеют относительно низкую структурную скрытность. Под скрытностью в криптографии понимают способность противостоять мерам радиотехнической разведки: обнаружению сигнала и определению его структуры на основе оценки ряда его параметров [2]. В нашем случае надо понимать этот термин в широком смысле – как меру хаотичности и случайности. Более высокую структурную скрытность – то есть непредсказуемость – имеют нелинейные последовательности, которые формируются регистрами сдвига с нелинейными обратными связями, например схемой «И». Нелинейная обратная связь допускает нахождение всех разрядов регистра сдвига в нулевом состоянии и обеспечивает выход генератора из него. Это принципиально важно при моделировании редко повторяющихся событий, характерных для сферы безопасности, то есть когда основным состоянием процесса является отсутствие событий.
При предлагаемой имитационной модели в качестве исходного генератора событий предлагается использовать ГСПЧ, реализованный на встроенном в программе Multisim источнике теплового шума V1 и компараторе, реализующем пороговую обработку (рис. 1). При изменении напряжения опорного источника V3, определяющего порог срабатывания компаратора, изменяется интенсивность потока событий.
Получение необходимого количества некоррелированных друг с другом ГСПЧ реализуется схемами задержки с нелинейными обратными связями, имеющими ответвления между двумя линиями задержки (ЛЗ) со случайно выбранными длительностями.
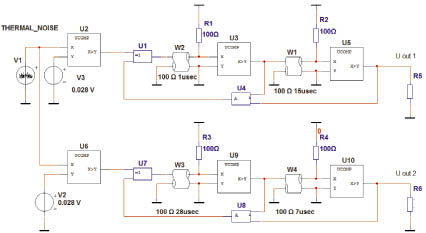
Рис. 2. Схема двух каналов ГСПЧ