Одной из негативных тенденций, осложняющей дальнейшее освоение и использование околоземного космического пространства (ОКП) в интересах населения Земли, является тенденция его загрязнения техногенным мусором или так называемым, космическим мусором (КМ) [1]. На протяжении всей космической эры, начиная с 1957 года по настоящее время, степень засоренности ОКП неуклонно возрастала и будет продолжать расти, даже если полностью прекратить запуски космических аппаратов (КА). Этому в определенной мере способствует «подключение» нового механизма формирования КМ, связанного с «размножением» КМ за счет разрушения крупных фрагментов мусора при их неупругом столкновении или столкновении с действующими КА. Этот эффект (впервые описанный Дональдом Кесслером в 1978 году [7]) получил название эффекта каскадного размножения Кесслера. Механизм каскадного размножения Кесслера запускается при достижении плотностью КМ критического значения, после чего количество фрагментов увеличивается по экспоненте. Со временем процесс размножения КМ замедляется по причине уменьшения числа относительно крупных фрагментов мусора и связанного с этим преобладания упругого столкновения над неупругим.
Целью настоящего исследования является построение математической модели прогнозирования предельного срока «экологической жизни» околоземных орбит в условиях прогрессирующего размножения космического мусора в соответствии с эффектом Кесслера.
Можно выделить три стадии формирования космического мусора: I – стадию накопления критической плотности КМ, II – стадию каскадного размножения КМ и III – стадию стабилизации плотности КМ.
Первая стадия характеризуется относительно невысокой скоростью роста числа объектов космического мусора (ОКМ). Причинами появления ОКМ на данной стадии являются: процессы эрозии внешних элементов конструкции КА; отделившиеся в процессе вывода КА на орбиту и не сгоревшие в плотных слоях атмосферы составные части ракет-носителей, разгонных блоков; осколки взорвавшихся на орбите КА; технологические элементы оборудования, случайно отделившиеся от орбитальных станций в процессе выполнения работ в открытом космосе; фрагменты КА, разрушенных в ходе испытаний средств поражения военного назначения. На второй стадии наблюдается ускорение процесса образования ОКМ за счет столкновения крупных фрагментов КМ с разрушением последних. Третья стадия характерна для ситуации, когда подавляющее большинство крупных фрагментов КМ разрушено, новые КА на рассматриваемую орбиту не выводятся, а мелкие фрагменты сталкиваются, не образуя осколков.
В зависимости от стадии скорость Vρ(t) возрастания плотности ОКМ ρ(t) во времени изменяется нелинейно, т.е. сначала возрастает, затем уменьшается до нуля. В то же время для удельной скорости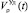 
, равной 
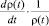, характерен линейный вид зависимости. Удельная скорость роста плотности ОКМ, равная в начальный момент r, по мере роста плотности ОКМ снижается, и при ρ(t) = P становится равной нулю, т.е. процесс размножения ОКМ останавливается, а плотность ОКМ стабилизируется, асимптотически приближаясь к числу P. Эта зависимость математически может быть записана в виде уравнения
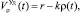(1)
где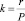 
, где r – начальное значение удельной скорости возрастания плотности ОКМ, фиксируемое на момент начала первой стадии; P – максимальное установившееся значение плотности ОКМ по завершении третьей стадии
Приняв во внимание, что
,
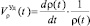можно записать
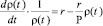(2)
или
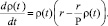(3)
Уравнение (3) носит название уравнения Ферхюльста, впервые примененного бельгийским математиком П. Ферхюльстом в 1838 году для описания роста численности населения.
Решив дифференциальное уравнение (3), получаем логистическую кривую [3].
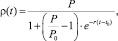(4)
где P0 – начальное значение плотности ОКМ, фиксируемое на момент t0 начала первой стадии.
Можно найти координату точки перегиба функции (4):
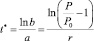
и значение функции (4) в этой точке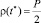 
.
Введем параметр PПред, равный предельному значению плотности ОКМ, при достижении которого использование околоземной орбиты становится невозможным по критериям опасности или нерентабельности затрат на защиту КА от ОКМ.
Предельным сроком «экологической жизни» TС.Ж околоземной орбиты будем называть интервал времени от начала ее использования до достижения предельного уровня PПред загрязнения орбиты КМ.
Составим и решим относительно TС.Ж следующее уравнение:
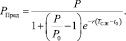(5)
Откуда
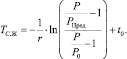(6)
Окончание использования околоземной орбиты зависит от возможностей КА противостоять воздействию потока высокоэнергетических частиц КМ. При этом надо учитывать, что средства защиты с течением времени развиваются и включают в себя как пассивные, так и активные средства, построенные на различных физических принципах. Стоимость таких средств защиты различна, эффективность также отличается. Все это приводит к тому, что трудно назначить устраивающее всех конкретное значение PПред. В связи с чем выходом из положения может быть отказ от назначения одного фиксированного значения предельного уровня PПред загрязнения орбиты в пользу рассмотрения некоторого спектра значений PПред, отличающихся по степени предпочтительности [4–6].
Математически такую идею можно реализовать, если использовать возможности теории нечетких множеств (ТНМ). С позиций ТНМ предельный уровень PПред загрязнения орбиты космическим мусором зададим в виде нечеткого множества (НМ):
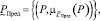(7)
функция принадлежности (ФП)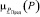 
которого имеет треугольную форму и описывается в аналитическом виде как
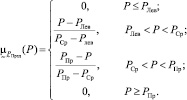(8)
С учетом (8) НМ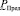 
можно кратко записать в виде тройки параметров:
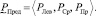(9)
Рассчитаем предельный срок «экологической жизни» околоземной орбиты при нечетком задании предельного уровня загрязнения орбиты космическим мусором. Для этого подставим (7) в формулу (6):
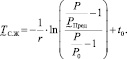(10)
В выражении (10) необходимо произвести ряд операций над нечеткой величиной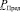 
. Л. Заде в работе [2] предложен способ нахождения произвольных функций от нечетких аргументов, который называется «принцип обобщения Л. Заде». В нашем случае, когда должна быть вычислена функция вида (10) от одного нечеткого аргумента 
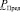, применяя принцип обобщения Л. Заде, получаем правило: результат нахождения функции вида (10) от нечеткого аргумента 
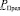есть нечеткая величина 
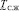, значения которой рассчитываются по формуле (6), а функция принадлежности совпадает с функцией принадлежности нечеткого аргумента 
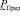(8).
Математически это правило можно записать следующим образом:
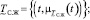
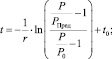
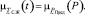(11)
В случае с треугольной функцией принадлежности вида (8) по аналогии с (9) ФП НМ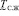 
можно записать в виде
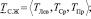(12)
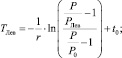
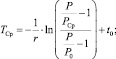
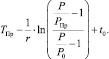
Наиболее наглядно изложенный выше способ прогнозирования предельного срока «экологической жизни» околоземной орбиты при нечетком задании предельного уровня загрязнения орбиты КМ показан на рис. 1.
Способ нечеткого прогнозирования предельного срока «экологической жизни» околоземной орбиты более адекватно учитывает вид фактической неопределенности информации о значении предельного уровня загрязнения орбиты космическим мусором. Однако нечеткость результата прогнозирования не всегда удобна для практического использования. В связи с этим исследуем вопрос возможности преобразования нечеткой оценки предельного срока «экологической жизни» околоземной орбиты к четкому виду.
В теории нечетких множеств существует операция нахождения альфа-сечения НМ, позволяющая преобразовать нечеткое множество к четкому.
Альфа-сечением Aα нечеткого множества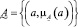 
называется обычное, то есть четкое подмножество, определяемое формулой 
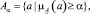α ∈ [0; 1]. Принцип нахождения альфа-сечения показан на рис. 2.
В зависимости от выбора конкретного значения α могут быть найдены различные множества Tα. Очевидно, что необходимо выбирать значение α не произвольно, а некоторым оптимальным способом.
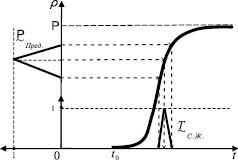
Рис. 1. Способ нечеткого прогнозирования предельного срока «экологической жизни» околоземной орбиты
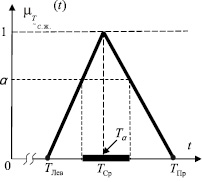
Рис. 2. Нахождение альфа-сечения Tα нечеткого множества предельного срока «экологической жизни» околоземной орбиты
Будем руководствоваться следующим правилом выбора. Чтобы наилучшим способом преобразовать НМ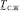 
к четкому множеству, необходимо выбрать такое значение α*, при котором четкое множество 
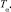наиболее близко к рассматриваемому НМ. В теории нечетких множеств доказано, что для того, чтобы наилучшим способом преобразовать НМ 
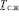к четкому множеству, необходимо выбрать значение α* = 0,5. Полученное описанным способом четкое множество T0,5 есть интервальная оценка момента окончания срока «экологической жизни» TС.Ж околоземной орбиты по критерию ее загрязнения космическим мусором.
Заключение
В работе получены аналитические выражения для прогнозирования срока «экологической жизни» орбит космических аппаратов с учетом прогрессирующей по закону Кесслера засоренности околоземного космического пространства техногенным мусором.
Предполагается, что срок «экологической жизни» космической орбиты заканчивается, когда описываемая логистической кривой плотность КМ достигает некоторого предельного уровня. Показано, что величина данного предельного уровня зависит от нескольких факторов, в частности от развития степени защиты КА от КМ, и не может быть задана в виде фиксированного значения плотности. Предложено описывать предельное значение плотности КМ нечеткой величиной, задаваемой экспертно. При этом результат прогнозирования срока окончания «экологической жизни» космической орбиты есть нечеткий интервал времени, который в данной работе предложено преобразовывать в обычный четкий интервал методом оптимального вписывания прямоугольника в треугольную функцию принадлежности нечеткого интервала времени.
Разработанный способ отличается простотой и наглядностью и может служить основой получения предварительных оценок срока «экологической жизни» орбит КА, которые затем можно уточнять с помощью более сложных и более дорогих программно-моделирующих комплексов.
Рецензенты:
Козлов В.В., д.т.н., профессор кафедры, Военно-космическая академия имени А.Ф. Можайского, г. Санкт-Петербург;
Садин Д.В., д.т.н., профессор кафедры, Военно-космическая академия имени А.Ф. Можайского, г. Санкт-Петербург.