Планирование экспериментов для нахождения оптимального значения функции отклика и получения аппроксимирующего полинома, описывающего поверхность функции отклика, традиционно является основой проектирования сухих строительных смесей различного назначения [1, 5]. Нахождение рационального состава современных многокомпонентных смесей с обеспечением нескольких критериев требуемого уровня качества подразумевает выполнение существенного количества физических экспериментов. Это делает данный процесс неэффективным, особенно в том случае, когда необходимо решить задачу нахождения оптимального состава материала с большим количеством переменных при наличии жестких граничных условий в сжатые сроки (например, при подборе состава реставрационных смесей).
Целью данной работы явилась разработка методики проектирования сухих строительных смесей, позволяющей минимизировать требуемое количество экспериментов.
Математические методы оптимизации имеют давние исторические корни. Их основы заложены в 18 веке – это вариационное исчисление, численные методы и др. К настоящему времени разработано большое количество методов, направленных на решение оптимизационных задач [2–4].
Для оптимизации может использоваться математическая модель исследуемого процесса (объекта) или сам объект. В последнем случае оптимизация производится опытным путем.
Для объектов вероятностного характера, к которым можно отнести многие строительные материалы, используются экспериментально-статистические методы, которые позволяют определить значения факторов (аргументов), соответствующих экстремальным значениям целевой функции.
При оптимизации опытным путем наиболее часто используются такие методы, как симплексный, покоординатной оптимизации, градиентные, деформируемого многогранника и некоторые другие.
Постановка задачи
Анализ методов оптимизации различных объектов опытным путем показывает, что достижение поставленной цели во всех методах представляет собой пошаговый процесс постепенного приближения к оптимуму. Их использование напрямую к оптимизации многокомпонентных составов сухих строительных смесей является нереальным ввиду большой продолжительности экспериментальных исследований, обусловленной чисто технологическими причинами.
Основной идеей, лежащей в основе предлагаемой методики, является использование для оптимизации экспериментально получаемой математической модели в виде целевой функции, описывающей зависимость параметров физико-механических свойств материала или других критериев оптимизации от количественного соотношения компонентов сухой смеси. Нахождение оптимума полученной целевой функции предлагается производить симплексным или иным численным методом с использованием численного моделирования с помощью специально разработанной программы для ЭВМ, реализующей математические модели, установленные экспериментально.
Предлагаемая методика включает в себя следующие этапы:
1. Выбор критерия оптимальности, определение области факторного пространства и ограничений, накладываемых на целевую функцию. В качестве критериев могут выступать как параметры физико-механических свойств строительных материалов, так и экономические, технологические и иные параметры.
2. Планирование и проведение экспериментов для получения уравнений регрессии, аппроксимирующих поверхности отклика в пределах заданного факторного пространства.
3. Выбор метода оптимизации, позволяющего найти экстремальные значения целевой функции. При решении этого вопроса возможно использование любого численного метода. На данном этапе планируется использование симплексного метода с учетом особенностей использования результатов численных экспериментов с использованием ЭВМ.
4. Реализация выбранного метода оптимизации с использованием результатов численных экспериментов по найденной математической модели и определение значений факторов (состава смеси), соответствующих оптимальным значениям целевой функции.
5. Экспериментальная проверка физико-механических свойств найденного состава.
Сокращение времени экспериментальных исследований достигается за счет использования численного моделирования целевой функции в процессе оптимизации. Основной объем экспериментальных исследований связан с получением математических моделей – аппроксимирующих полиномов (уравнений регрессии) и может быть проведен в сравнительно сжатые сроки.
Оценка эффективности предлагаемой методики оптимизации
Оценка эффективности предлагаемой методики осуществлялась следующим образом.
Выбиралась математическая модель в виде уравнения регрессии, подобного тем, что обычно получаются при исследовании свойств строительных материалов. В это уравнение вводилась добавка – случайная величина, распределенная по нормальному закону и имитирующая различные погрешности, возникающие при проведении реальных экспериментов. Эта модель реализовывалась на ЭВМ с помощью специально разработанной программы, позволяющей производить численные эксперименты с указанной моделью.
Далее считалось, что указанная выше модель неизвестна, и ставилась задача определить максимум исследуемой целевой функции в заданных пределах факторного пространства, используя пошаговый метод оптимизации – метод крутого восхождения. Все это понадобилось для того, чтобы определить потребное количество экспериментов, необходимое для решения поставленной задачи.
Затем, тоже в целях определения потребного количества опытов, устанавливался вид исследуемой целевой функции. Полученная математическая модель использовалась для определения максимума целевой функции с использованием симплексного метода.
При использовании выбранного метода доказательства эффективности предлагаемой методики важным моментом является обеспечение наглядности получаемых результатов – как промежуточных, так и окончательных. В связи с этим в качестве математической модели исследуемого процесса выбран двухфакторный полином второй степени вида
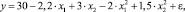 (1)
(1)
где y – функция отклика (целевая функция при оптимизации); x1 и x2 – факторы, влияющие на нее, ε – погрешность, распределенная по нормальному закону.
Функция y гладкая, непрерывная и определена в области положительных значений. Последнее условие реализовано выбором ограничений факторов (факторного пространства).
Исследование функции (1) показало, что она не имеет экстремума. То есть в данном случае задача оптимизации должна сводиться к определению максимальных значений этой функции в пределах заданного факторного пространства. Наибольшее значение выбранная функция имеет при минимальном значении x1 = 2,3 и максимальном x2 = 3,84. Все это должно было подтвердиться при исследовании этой функции методами планирования экспериментов.
Нахождение экстремума исследуемой функции методом крутого восхождения показало, что максимальные значения целевой функции действительно соответствуют следующим значениям факторов x1 = 2,3 и x2 = 3,84. Начальная область, используемая для определения градиента, располагалась посередине факторного пространства.
При определении вида целевой функции (уравнения регрессии) методами планирования экспериментов, исходили из того, что исследуемая зависимость, как отмечалось ранее, неизвестна. Ввиду этого вначале предполагалось, что математическая модель представляет собой линейный полином. Статистический анализ данной модели показал, что она неадекватна, и поэтому был выбран полином второго порядка.
Полученное адекватное уравнение регрессии в кодированных значениях факторов со статистически значимыми коэффициентами имеет вид
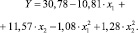 (2)
(2)
В действительных переменных:
 (3)
(3)
Сравнение полученного уравнения регрессии (3) с исходным (1) показывает, что уравнения очень близки – небольшое расхождение объясняется наложением «шума».
При нахождении максимума исследуемой целевой функции с использованием полученного уравнения регрессии (2) и симплексного метода полагалось, что начальная точка, с которой начинается поиск максимума, находится посередине факторного пространства (как и при использовании метода крутого восхождения). Реализация симплексного метода с использованием результатов численного моделирования по уравнению (2) показала, что максимальные значения функции Y соответствуют значениям факторов x1 = 2,3 и x2 = 3,84.
По результатам нахождения максимума двухфакторной функции отклика различными методами установлено следующее. При использовании метода крутого восхождения искомый максимум найден, с учетом проверки наличия максимума в окрестности точки предполагаемого максимума, по результатам 22 опытов. Без учета проверки – за 13 опытов. При использовании симплексного метода, оптимум найден за 16 опытов. Количество же реальных экспериментов для получения уравнения регрессии в виде полинома второй степени составило 7. Таким образом, использование предлагаемой методики для двухфакторного эксперимента позволяет в два раза сократить количество реальных опытов. Очевидно, что такой результат сохранится и при увеличении числа факторов.
Если рассматривать эффективность предлагаемой методики с точки зрения продолжительности испытаний, то эффект оказывается еще большим. Например, если полагать, что для набора прочности цементной композиции требуется 28 дней (то есть на один реальный опыт практически один месяц), то для нахождения максимума функции отклика по прочности образцов градиентным пошаговым методом потребуется 1 год. При использовании предлагаемой методики этот срок может сократиться до двух-трех месяцев с учетом экспериментального подтверждения найденного максимума.
Заключение
В работе предложен подход, позволяющий эффективно решать задачу оптимального проектирования многокомпонентных композиционных материалов на основе применения методов численного моделирования. Предлагаемая методика позволяет в достаточно сжатые сроки за счет значительного снижения количества натурных экспериментов (минимум в два раза) разработать материал, свойства которого максимально соответствуют ключевым проектным данным.
Рецензенты:
Пухаренко Ю.В., д.т.н., профессор, заведующий кафедрой технологии строительных материалов и метрологии, ФГБОУ ВПО «Санкт-Петербургский государственный архитектурно-строительный университет», г. Санкт-Петербург;
Шангина Н.Н., д.т.н., профессор кафедры технологии строительных материалов, ФГБОУ ВПО «Петербургский государственный университет путей сообщения», г. Санкт-Петербург.



