На кафедре машин и оборудования в агробизнесе Казанского ГАУ была разработана и создана пневмомеханическая семенорушка, позволяющая реализовывать технологию переработки семян подсолнечника непосредственно на базе сельскохозяйственных предприятий различной формы организации [2…5]. Семенорушка содержит питающий бункер 1 с загрузочным патрубком, вентилятор-метатель 2 с электродвигателем 3, вертикальный осадитель 4 с вытяжной трубой 5, рабочую пластину 6, сетчатый рабочий орган 7, раму 8 (рис. 1).
В пневмомеханической семенорушке воздушно-зерновая смесь, подаваемая вентилятором-метателем, сталкивается с рабочим органом в виде полусферы [4, 5]. При этом происходит обрушивание – отделение оболочки от ядрицы.
Для оценки эффективности технологического процесса обрушивания используются два показателя: количественный (K0) и качественный (Kц.я) [4]:
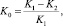(1)
где K0 – коэффициент обрушивания; K1 – содержание необрушенных семян до поступления в семенорушку, %; K2 – содержание необрушенных семян после однократного пропуска через семенорушку, %.
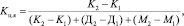(2)
где Kц.я – коэффициент цельности ядра; K2 – K1 – разность в содержании целых ядер до и после обрушивания, %; Д2 – Д1 – разность в содержании дробленых ядер до и после обрушивания, %; М2 – М1 – разность в содержании мучки в продукте до и после обрушивания, %.
Эти показатели зависят от частоты вращения ротора вентилятора-метателя (контролируемый параметр (п)), и от случайного фактора – наклона осей семян (от тупого к острому концу) к рабочей пластине. Этот угол (α) может быть в пределах от 0 до π.
Целью работы является определение зависимости Кц.я от наклона осей семян (α) и частоты вращения ротора вентилятора-метателя (п).
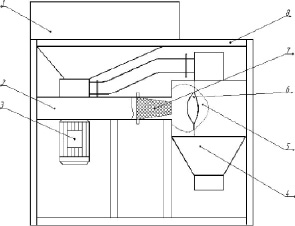
Рис. 1. Общий вид пневмомеханической семенорушки: 1 – бункер с питающим патрубком; 2 – бросковый вентилятор; 3 – электродвигатель; 4 – осадитель; 5 – труба вытяжная; 6 – сферическая рабочая пластина; 7 – сетчатый рабочий орган; 8 – рама
Материалы и методы исследования
Так как выбор режима из числа возможных происходит в условиях неопределенности в отношении угла α, наиболее приемлемым является так называемый максиминный критерий, ориентирующий на принятие наилучшего варианта в наихудших условиях [1].
Результаты исследования и их обсуждение
Для использования данного метода нами были проведены ряд экспериментов на специально изготовленной семенорушке, где возможно осуществить два режима работы с числом оборотов ротора 1000 и 1200 мин–1. В каждом режиме стограммовая порция откалиброванных по длине и ширине семян пропускалась через калибровочное решето с круглыми отверстиями наименьшего диаметра, примыкающими друг к другу, так что через них могли пролететь лишь семена с углом α = 0…30°. Затем подсчитывалось количество цельных ядриц. Опыт повторяли с решетом, через отверстия которого пролетали семена с углом наклона оси до 60°, и проводились такие же подсчеты. Вычитание из значения Кц.я во втором опыте значения Кц.я в первом опыте дает нужную цифру для семян с углами наклона оси от 30 до 60° и т.д. Экран располагался на расстоянии 2 см от решета.
В серии экспериментов нами были получены различные значения Кц.я, округленные до целого числа процентов.
Результаты экспериментов приведены в таблице.
Для рассматриваемой задачи допускаем, что часть времени p1 из всего времени работы семенорушки протекает с частотой вращения ротора 1000 мин–1, а часть p2 = 1 – p – с частотой вращения – 1200 мин–1. Такое сочетание дает соответствующий смешанный режим обрушивания семян.
В дальнейшем ввиду непрерывности значений α, отнесем их к левым значениям α, т.е. к α = 0; π/6; π/3; π/2; 2π/3; 5π/6 (αj, j ∈ {1, ..., 6}).
Результаты экспериментов
|
п, мин–1 |
α, рад |
|||||
|
0 ≤ α < π/6 |
π/6 ≤ α < π/3 |
π/3 ≤ α < π/2 |
π/2 ≤ α < 2π/3 |
2π/3 ≤ α < 5π/6 |
5π/6 ≤ α < π |
|
|
1000 |
8 |
13 |
18 |
35 |
20 |
6 |
|
1200 |
2 |
12 |
21 |
27 |
28 |
10 |
Известно [1], что в подобной ситуации, когда из-за непредсказуемости неконтролируемой величины нельзя отдать предпочтение тому или иному нашему выбору, а в отношении указанной величины α нет даже вероятностей оценки её значений (как и оснований считать их равновероятными), наиболее приемлемым по ряду соображений является максиминный критерий, ориентирующий на принятие наилучшего варианта в наихудших условиях.
Математически это означает, что рекомендуется выбрать то i (для приведенной таблицы i ∈ {1; 2}), при котором достигается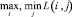 
для этой таблицы j ∈ {1, ..., 6}).
То, что выше значения α в соответствующих интервалах были заменены их наименьшими значениями, а не какими-то другими, не играет роли. Это стандартная процедура. Достаточно вспомнить, например, что в сущности то же самое делается при приближенном вычислении определенного интеграла по формуле прямоугольников.
Можно добиться и увеличения выигрыша, если допустить некие смеси вариантов с весами pi и qj и вместо функции L(i, j) рассматривать её математическое ожидание
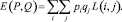
Тогда оптимальным будет выбор, обеспечивающий
,
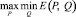где P и Q – все возможные распределения весов piqj. Для нашей таблицы это все симплексы P(p1, p2), Q(q1, q2, ..., q6). Здесь все piqj ≥ 0,
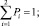
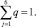
Оптимальным при этом будет некоторый P0. (У нас P0(p10, p20)). Большего, однако, добиться не удастся, т.к. известно, что
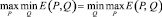
и неравенство
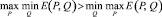
невозможно.
Иными словами, достигаемое при этом равенство максимина минимаксу равносильно выполнению соотношений E(P, Q0) ≤ E(P0, Q0), E(P, Q0) ≥ E(P0, Q0), где P0, Q0 – это те P, Q, для которых максимин равен минимаксу. Из двух последних неравенств видно, что существует такое значение ϑ = E(P0, Q0), что если отступить от оптимального выбора, взяв P отличным от P0, то выигрыш по сравнению с ϑ может только уменьшиться. Аналогично, если окажется, что Q ≠ Q0, то выигрыш при выборе именно P0 (по сравнению с ϑ) может только возрасти. Нахождение P0, Q0 и ϑ – есть цель решения математической задачи.
Величины pi, pj при этом могут интерпретироваться по-разному, но естественным для данной технической задачи образом. Что касается весов qi, то их введение соответствует углу α, вычисляемому как среднее из значений αi, т.е.
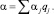
Вычисление P0, Q0, ϑ в общем случае для матрицы произвольных размеров (m×n) (m1n > 2) производится на компьютере по одной из стандартных программ решения так называемых матричных игр, например на основе алгоритма решения пары двойственных задач выбора решения в условиях неопределенности, в информативном отношении для принимающего решения лица эквивалентна такой игре.
Для рассматриваемой технической задачи, ввиду наличия у нас всего двух «чистых стратегий», как такое решение осуществляется, будет показано ниже. Пока же остановимся на том, как были получены элементы матрицы.
Обозначим p1 = x. Тогда p2 = 1 –x x ∈ [0; 1].
Для ожидаемых выигрышей получены следующие уравнения:
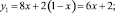
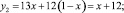
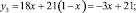(3)
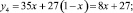
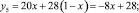
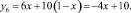
Графические изображения полученных уравнений представлены на рис. 2.
Минимальная кривая здесь – ломаная из отрезков прямых y1(x), y6(x) (на рис. 2 – жирным). Её вершина в точке х, определяемой системой уравнений
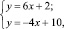(4)
т.е. при х = 0,8. Таким образом, оптимально 0,8 времени работать с частотой вращения – 1000 мин–1 и 0,2 – с частотой – 1200 мин–1. При этом ожидаемый процент обрушенных семян составит 6∙0,8 + 2 = 6,8.
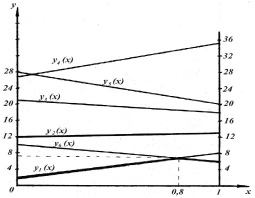
Рис. 2. Зависимости ожидаемых выигрышей
Итак, t10 = 0,8; Kия = 6,8. В решении оказались неучаствующими столбцы матрицы со второго по пятый. Поэтому, исключая их, можно сказать, что исходная матрица эквивалентна следующей:
Но тогда должно быть:
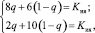(5)
где q = q10; q20 = q30 = q40 = q50 = 0; q60 = 1 – q.
Любое из этих уравнений дает q = 0,4. Это значит, что самым нежелательным является угол
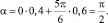
Вывод
Для достижения наибольшего значения коэффициента извлечения цельных ядер конструктивное исполнение семенорушек должно обеспечивать соударение семян с рабочей пластиной в направлении продольной оси.
Рецензенты:
Галиев И.Г., д.т.н., профессор кафедры инженерного менеджмента, Казанский государственный аграрный университет, г. Казань;
Яхин С.М., д.т.н., профессор кафедры общеинженерных дисциплин, Казанский государственный аграрный университет, г. Казань.