В кризисные для экономики периоды сколько-нибудь точно предсказать развитие экономических процессов становится сложнее, при этом, естественно, ценность получения качественных прогнозов повышается.
В данной статье отражены результаты использования эконометрических и статистических подходов к прогнозированию макроэкономических стабилизационных процессов в России на основе построенных моделей временных рядов показателей, характеризующих исследуемые процессы. Чтобы оценить возможности использования построенных эконометрических моделей для прогнозирования рассматриваемых процессов, в работе предложен критерий точности прогнозирования и проведено сравнение прогнозных возможностей полученных авторегрессионных моделей и системы одновременных регрессионных уравнений, также выполнено точечное прогнозирование значений показателей исследуемых макроэкономических процессов.
В соответствии с основными признаками стабильного состояния экономики России [4, 5, 6] для прогнозирования макроэкономических стабилизационных процессов были выбраны следующие, определяющие эти признаки, экономические показатели (эндогенные переменные): Y(1) – индекс промышленного производства (% к соответствующему периоду предыдущего года); Y(2) – общая численность безработных на конец периода (млн чел.); Y(3) – чистый экспорт (млрд долл. США); Y(4) – индекс потребительских цен (% к соответствующему периоду предыдущего года); Y(5) – начисленная среднемесячная заработная плата одного работника номинальная (% к соответствующему периоду предыдущего года); Y(6) – инвестиции в основной капитал (% к соответствующему периоду предыдущего года).
При формировании информационной базы исследования использовались официальные данные электронного издания «Краткосрочные экономические показатели Российской Федерации», которые ежемесячно размещаются на сайте Федеральной службы государственной статистики. Информация по всем рассматриваемым в данной статье экономическим показателям, представляющим собой временные ряды, включает статистические данные за 16,5лет (по месяцам): с января 1999г. по июнь 2015г. (198наблюдений по каждому временному ряду). Обработка и анализ статистической информации проводились с использованием пакетов программ EViews, Statistica, MS Excel.
На этапе предварительного анализа было проведено исследование временных рядов макроэкономических показателей на наличие в них сезонной компоненты, а также на стационарность. По графикам исходных уровней, автокорреляционной функции (АКФ) и частной автокорреляционной функции (ЧАКФ) временных рядов исследуемых показателей был сделан вывод об отсутствии сезонной компоненты. Исследование стационарности рассматриваемых рядов на основании расширенного (пополненного) теста Дикки – Фуллера (ADF-тест) [2] показало, что временные ряды анализируемых показателей не являются стационарными, а первые разности их уровней стационарны. Следовательно, исходные временные ряды являются интегрированными первого порядка (I(1)).
После проведенного предварительного анализа, учитывая нестационарность временных рядов рассматриваемых показателей, для осуществления прогнозирования значений этих показателей были построены следующие эконометрические модели: авторегрессионные модели, включая интегрированные модели авторегрессии и скользящего среднего (ARIMA) и модели векторной авторегрессии (VAR), а также система одновременных уравнений (СОУ).
На этапе построения моделей ARIMA(p, d, q)(где p, d, q – соответственно порядки авторегрессии, интегрированности и скользящего среднего) для каждого временного ряда исследуемых показателей были подобраны возможные порядки авторегрессии и скользящего среднего [3]. Для этого строились графики АКФ и ЧАКФ каждого стационарного временного ряда (ряда первых разностей), анализ которых позволил сделать вывод, что рассматриваемые временные ряды показателей лучше всего (со стационарными и некоррелированными остатками и наименьшим числом параметров) описываются моделью ARIMA(1,1,0). Врезультате построения и оценивания соответствующих параметров для временного ряда каждого показателя Y(i),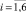 
(перейдя от первых разностей к исходным уровням) были получены следующие модели со статистически значимыми оценками их параметров (за исключением некоторых оценок свободных членов):
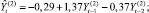
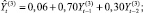
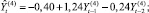
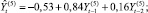
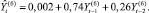
Для построения модели векторной авторегрессии (VAR) [4, 7] в качестве переменных (эндогенных) были рассмотрены все перечисленные (преобразованные к стационарному виду) показатели Y(i),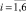 
, и каждая переменная моделировалась как функция от лаговых значений всех упомянутых переменных. Чтобы определить наибольшую длину лага p переменных, которые войдут в модель, строилось несколько моделей с различным значением p. Наибольшая длина лага p, равная 3месяцам, была определена на основе критериев Акаике и Шварца и проверки статистической значимости оценок параметров соответствующих переменных модели (отдельно и всовокупности). Таким образом была построена система из шести уравнений (по количеству эндогенных переменных), каждое из которых определяет зависимость каждой переменной от лаговых значений (с лагом 1, 2, 3месяца) всех рассмотренных (преобразованных к стационарному виду) переменных. Лаговые переменные со статистически незначимыми оценками параметров были исключены из модели (незначимость оценок может означать, что переменная с данным лагом не оказывает существенного влияния на динамику соответствующего показателя). Врезультате получена следующая модель:
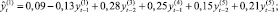
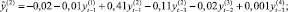
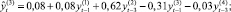
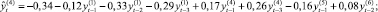
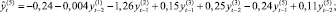
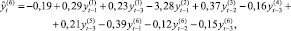
где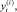 
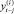– преобразованные к стационарному виду текущие и лаговые переменные;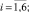 
Авторегрессионные модели достаточно широко используются для прогнозирования (вэтом и заключается главная цель построения таких моделей). Однако, для всестороннего анализа и моделирования взаимосвязей рассмотренных показателей, а также их связей с другими показателями (экзогенными переменными), и далее для прогнозирования была получена и структурная модель в виде системы одновременных (регрессионных) уравнений.
Для построения системы одновременных уравнений (СОУ) (учитывая результаты использования теста Грэнжера на определение причинно-следственной зависимости с рассмотренными эндогенными переменными, исследования устойчивости всех временных рядов, а затем и проведения коинтеграционного анализа [2, 9]) были отобраны в качестве экзогенных переменных следующие показатели: X(1) – коммерческий грузооборот транспорта (млрдт-км); X(2) – погрузка грузов на железнодорожном транспорте (млнт); X(3) – объем работ по виду деятельности «Строительство» (млрдруб.); X(4) – официальный курс доллара (руб. за 1долл. США); X(5) – оборот розничной торговли (млрд руб.); X(6) – объем платных услуг населению (млрдруб.); X(7) – денежные доходы в среднем на душу населения (руб.); X(8) – просроченная кредиторская задолженность организаций в бюджет (млрдруб.); X(9) – просроченная дебиторская задолженность организаций (млрдруб.); X(10) – средние цены производителей на нефть (руб. за 1т); X(11) – средние цены производителей на газ горючий (руб. за 1тыс.м3).
Временные ряды всех отобранных экзогенных переменных также были проверены на наличие в них сезонной компоненты. Врезультате у переменных X(1), X(2), X(3), X(5), X(6) и X(7) сезонная компонента была обнаружена и устранена. При исследовании стационарности временных рядов экзогенных переменных по результатам ADF-теста было получено, что все ряды являются интегрированными первого порядка (I(1)). Одинаковый порядок интегрированности временных рядов переменных для СОУ позволил осуществить проверку данных рядов на наличие коинтеграции. Коинтеграционный анализ проводился для пар временных рядов экзогенных и эндогенных переменных, у которых была выявлена причинно-следственная зависимость. Для проверки гипотезы о наличии коинтеграции применялся метод Энгла – Грэнжера [2]. Проверка показала, что пары рассмотренных временных рядов экономических показателей коинтегрированы. Полученные выводы позволили использовать при построении СОУ исходные уровни рассматриваемых рядов, учесть долговременную зависимость между показателями и получить надежный прогноз.
Используя результаты коинтеграционного анализа и проверив выполнимость условий идентифицируемости модели, была получена структурная форма СОУ. Врезультате оценивания ее структурных параметров (по выборке объемом n=198) получена следующая модель:
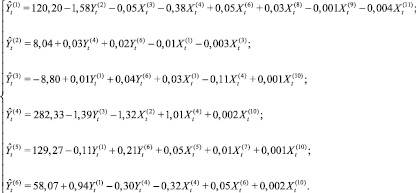
Анализ качества каждой из построенных моделей (ARIMA, VAR и СОУ) позволил сделать следующие выводы: все оценки параметров моделей ARIMA и большинство оценок параметров уравнений моделей VAR и СОУ статистически значимы по t-критерию на 5–10 %-ном уровне значимости; все модели статистически значимы по F-критерию на 10 %-номуровне значимости; анализ остатков уравнений моделей показал, что остатки имеют распределение, близкое к нормальному (анализировались построенные гистограммы, характеристики и результаты теста Жарка – Бера); отсутствует автокорреляция (использовался тест Бокса – Пирса) и гетероскедастичность остатков (использовался тест Уайта).
Все построенные эконометрические модели были проверены на возможность их использования для прогнозирования исследуемых макроэкономических процессов. Для сравнения прогнозных возможностей моделей по каждому показателю Y(i) (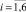
) было выполнено тестовое прогнозирование с помощью процедуры «скользящего экзамена» [1, 8]. Всоответствии с этой процедурой выбрано m=10 постпрогнозных точек внутри выборки (10значений (10месяцев) в конце временного ряда каждого показателя: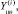 
…, 
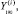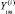). Каждая модель оценивалась по первым (n – m) наблюдениям и использовалась для получения прогнозного значения 
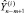. Далее модель переоценивалась вновь по первым (n – m+1) наблюдениям и вычислялось прогнозное значение 
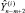и т.д. до нахождения последнего прогнозного значения 
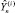. Эта процедура проводилась отдельно для каждой построенной эконометрической модели (ARIMA, VAR, СОУ). На рисунке представлено графическое изображение полученных описанным выше способом прогнозных значений показателя Y(1) по всем построенным моделям и соответствующие фактические значения этого показателя.
В качестве критерия точности прогнозирования всех построенных моделей для каждого i-го показателя использовалась средняя относительная ошибка прогноза:
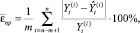
где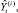 
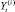– прогнозное значение, найденное с помощью процедуры «скользящего экзамена», и соответствующее фактическое значение показателя Y(i) (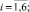
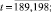n=198; m=10). Результаты вычислений 
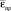приведены в табл.1.
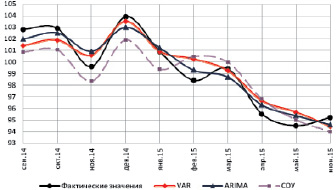
Результаты тестового прогнозирования с помощью процедуры «скользящего экзамена» значений показателя Y(1) (индекс промышленного производства, %) за период с сентября 2014г. по июнь 2015 г.
Таблица 1
Средние относительные ошибки прогноза (%) по 10-ти постпрогнозным точкам
|
Модели |
Показатели |
|||||
|
Y(1) |
Y(2) |
Y(3) |
Y(4) |
Y(5) |
Y(6) |
|
|
ARIMA |
0,96 |
2,66 |
7,74 |
0,88 |
1,51 |
2,34 |
|
VAR |
1,22 |
2,45 |
7,86 |
1,49 |
1,54 |
1,92 |
|
СОУ |
3,09 |
7,09 |
12,59 |
7,98 |
5,99 |
6,07 |
Таблица 2
Прогнозные значения показателей стабилизационных процессов на июль – декабрь 2015г.
|
Показатели |
Модели |
Июль |
Август |
Сентябрь |
Октябрь |
Ноябрь |
Декабрь |
|
Y(1) |
VAR |
95,29 |
95,38 |
95,27 |
95,14 |
94,94 |
94,88 |
|
ARIMA |
95,11 |
95,12 |
95,11 |
95,10 |
95,10 |
95,09 |
|
|
СОУ |
93,77 |
93,76 |
94,00 |
94,18 |
94,39 |
94,60 |
|
|
Y(2) |
VAR |
3,97 |
4,09 |
4,06 |
4,07 |
4,05 |
4,03 |
|
ARIMA |
4,01 |
3,96 |
3,92 |
3,89 |
3,86 |
3,83 |
|
|
СОУ |
4,22 |
4,19 |
4,17 |
4,15 |
4,13 |
4,12 |
|
|
Y(3) |
VAR |
14,45 |
13,52 |
13,64 |
13,51 |
13,66 |
13,69 |
|
ARIMA |
14,33 |
14,25 |
14,36 |
14,41 |
14,47 |
14,53 |
|
|
СОУ |
14,43 |
13,56 |
16,64 |
14,72 |
15,79 |
16,86 |
|
|
Y(4) |
VAR |
116,05 |
115,05 |
114,18 |
113,80 |
113,31 |
112,73 |
|
ARIMA |
114,88 |
114,47 |
114,07 |
113,67 |
113,27 |
112,87 |
|
|
СОУ |
109,32 |
112,00 |
113,72 |
114,46 |
112,21 |
110,95 |
|
|
Y(5) |
VAR |
105,95 |
104,63 |
104,67 |
104,44 |
104,18 |
103,96 |
|
ARIMA |
105,62 |
105,52 |
105,48 |
105,42 |
105,37 |
105,32 |
|
|
СОУ |
103,62 |
101,91 |
104,70 |
102,72 |
100,57 |
100,49 |
|
|
Y(6) |
VAR |
93,32 |
93,00 |
92,49 |
92,56 |
92,19 |
92,29 |
|
ARIMA |
92,77 |
92,81 |
92,80 |
92,81 |
92,81 |
92,81 |
|
|
СОУ |
94,93 |
94,71 |
94,63 |
94,46 |
94,30 |
94,14 |
Тестовое прогнозирование показателей анализируемых процессов на основе авторегрессионных моделей показало, что средние относительные ошибки прогноза большинства показателей по моделям ARIMA и VAR составили не более 3 % (кроме Y(3) – чистый экспорт). Это позволило сделать вывод, что построенные авторегрессионные модели и ARIMA, и VAR обладают хорошими прогнозными возможностями и являются достаточно надежными инструментами прогнозирования исследуемых показателей. Средние относительные ошибки прогноза, полученные на основе СОУ, по всем рассмотренным показателям больше, чем соответствующие значения по двум другим построенным моделям, но в основном не превышают 8 % (за исключением Y(3)). Несмотря на достаточно трудоемкий процесс построения и оценивания параметров структурной модели, модель в виде СОУ обладает очень важным преимуществом. Она позволяет всесторонне охватить и проанализировать экономические связи и взаимосвязи рассматриваемых показателей (эндогенных переменных) с другими показателями (экзогенными переменными) исследуемых экономических процессов, смоделировать структуру этих связей.
На основании результатов и выводов, полученных при моделировании и сравнении прогнозных возможностей построенных моделей, было выполнено прогнозирование показателей исследуемых стабилизационных макроэкономических процессов на следующие шесть месяцев (июль – декабрь 2015г.) по всем предложенным моделям (табл.2).