Одним из ключевых факторов улучшения финансового результата страховой компании является повышение эффективности использования проблемно-ориентированных систем сбора и обработки учетно-аналитической информации (СОУИ), обеспечивающих управление ее операционными бизнес-процессами: заключением и сопровождением договоров страхования, андеррайтингом и урегулированием убытков.
Под эффективностью использования в рассматриваемом контексте понимается соответствие функциональности построенных на основе СОУИ специализированных компонентов корпоративной информационной системы (КИС) компании установленным для данного класса ИТ-решений требованиям по обеспечению поддержки бизнес-задач операционной страховой деятельности.
Как показывает практика, эффективность использования СОУИ зависит от качества моделей функциональной оптимизации, применяемых на стадии концептуального проектирования систем.
В этой связи представляет актуальность научно-техническая проблема разработки подхода к формализованной постановке задач функциональной оптимизации страховых СОУИ, обеспечивающих высокую эффективность использования указанных систем.
Формально критерий эффективности использования страховой СОУИ по функциональности может быть описан как совокупность
К=(Кд, {Ко}),
где Кд – императивный критерий обеспечения достоверности, полноты и хронологической упорядоченности страховой информации; {Ко} – конечное множество критериев обеспечения информационной поддержки операционных бизнес-процессов страховой компании.
Сформулированные критерии представляют собой основу для формализованной постановки задач оптимизации страховых СОУИ, обеспечивающих поддержку операционных бизнес-процессов страховой компании.
Математическая модель страховой СОУИ
Вопросы обеспечения эффективности использования информационных систем страхового учета являются предметом исследования многих современных ученых. Однако в большинстве публикаций по данной проблематике, в частности в работе [5], не предлагаются какие-либо формализованные модели оценки и повышения эффективности использования таких систем, а представленные выводы ограничиваются описанием оптимального набора их функций. Вэтой связи заслуживают особого внимания методы формализации задач анализа и синтеза оптимальных автоматизированных информационно-управляющих систем, предлагаемые в работе [1]. Следует отметить, что представленные в ней математические модели носят обобщающий характер и не позволяют отразить специфические особенности обработки и контроля информации страхового учета.
Вместе с тем результаты представленных исследований подтверждают, что при моделировании СОУИ предпочтение следует отдавать методологиям, основанным на интеграции различных подходов и методов. Указанному требованию отвечает методология моделирования страховых СОУИ, опирающаяся на принципы объектно-структурного и автоматного подходов [3]. Согласно концепции, положенной в основу этой методологии, функциональность и принципы построения проблемно-ориентированных СОУИ позволяют рассматривать их как интегрированные с КИС предприятия дискретно-событийные имитационные модели информационно-логистических систем, обеспечивающие проведение вычислительных экспериментов с управленческим учетом на основе реальных первичных данных, в том числе накопленных за предыдущие периоды.
В основу методологии положено понятие объектно-структурной модели страховой СОУИ, которая для N-передельного процесса обработки учетно-аналитической информации описывается как линейное ориентированное дерево О (SP, SR, D) (рис.1), где:
SP={SP1, SPN+2} – узлы ориентированного дерева модели, обозначающие виртуальные страховые портфели;
SR={SR2, SR3, …, SRN+1} – узлы, обозначающие виртуальные переделы учетных страховых документов, которые представляют собой комбинацию объектов «Страховой портфель», «Страховой контролер» и «Страховой агрегат», обеспечивающие управление статусом обрабатываемого документа;
D={D1, D2, ..., DN+1} – нагруженные учетно-аналитической информацией дуги, обозначающие маршрут движения учетных документов.
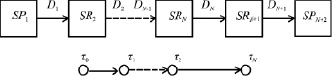
Рис. 1. Объектно-структурная модель N-передельной страховой СОУИ
С позиций автоматного подхода страховая СОУИ рассматривается как система электронного документооборота, модель которой представляет собой сеть из взаимодействующих конечных автоматов со шкалой времени, образованной метками учетной транзакции τ0, τ1, τ2, …, τN [2].
В рамках учетной транзакции автоматы сети могут взаимодействовать по принципу вызываемости: один автомат вызывается с определенным событием из выходного воздействия, формируемого при переходе другого автомата [4]. Иными словами, учетная транзакция запускается при поступлении на вход описанной сети последовательности из значений атрибутов страхового документа, одним из которых является статус документа, и далее выполняется по принципу «цепной реакции».
Предлагаемую сетевую модель автоматов можно описать как конечный автомат вида
S=<D1, DN+1, Q, δ, λ>,
где D1=(RD1, CD1) – данные страхового документа на входе автомата, где RD1 – реквизиты документа; CD1⊂ZD – статусы страхового документа на входе сети; ZD – конечное множество состояний жизненного цикла (ЖЦ) обрабатываемого страхового документа; DN+1=(RDN+1, CDN+1) – данные страхового документа на выходе автомата, где RDN+1 – реквизиты документа; CDN+1⊂ZD – статусы страхового документа на выходе сети; Q – конечное множество состояний автомата S; δ, λ – функции переходов и выходов автомата S, определяемые как композиции соответствующих функций конечных автоматов, образующих сеть:
δ(D1,Q)=δN+1(δN (…(δ2(D1,Q))…));
λ(D1,Q)=λN+1(λ N (…(λ 2(D1,Q))…)),
где δ2, δ3,…, δN+1 и λ2, λ3,…, λN+1 – функции переходов и выходов конечных автоматов – элементов рассматриваемой сети.
Если допустить, что в процессе выполнения транзакции изменениям подвергается только статус страхового документа, динамическая модель полученной сети для любого такта t=1, 2, …, N описывается следующим образом:
q(t)=δ[(rd1(t), cd1(t)), q(t – 1)];
cdN+1(t)=λ[(rd1(t), cd1(t)), q(t)].
Тогда математически задача функциональной оптимизации страховой СОУИ может быть описана как задача обхода ориентированного графа перехода статусов обрабатываемого страхового документа конечным автоматом S при ограничениях, накладываемых спецификой конкретного вида страхового учета.
Таким образом, задача страховой СОУИ, как имитационной модели, в общем виде сводится к реализации алгоритма изменения состояний автомата S в рамках учетной транзакции. Стоит отметить, что решение данной задачи существенно упрощается благодаря свойствам объектно-структурной модели СОУИ и использованию явно заданных графов переходов статусов обрабатываемого документа, построенных на основе его жизненного цикла.
Рассмотрим примеры постановок задач оптимизации проблемно-ориентированных страховых СОУИ, обеспечивающих поддержку операционных бизнес-процессов страховой компании.
Постановка задачи оценки достоверности информации страховой СОУИ
Как показывает практика, источниками ошибок в страховом учете являются нарушения правил учета и оформления первичной документации. Идентификация таких ошибок на входе и выходе СОУИ осуществляется с помощью метода форматно-логического контроля – проверки электронного документа на соответствие установленным для него требованиям по структуре и формату данных.
Рассмотрим формализацию постановки задачи оценки достоверности N-передельной страховой СОУИ.
Для этого введем понятие форматно-логической ошибки (ФЛО) страхового документа, которая идентифицируется при отклонении реального статуса документа на выходе передела объектно-структурной модели СОУИ от его истинного значения, задаваемого графом ЖЦ документа.
Допустимо утверждение, что в случайный момент времени на переделах объектно-структурной модели СОУИ может быть идентифицирована одна и только одна ФЛО, после чего должна произойти отмена учетной транзакции и аварийное завершение процесса обработки документа.
В современной практике операционной страховой деятельности основной характеристикой оценки достоверности информации страхового учета для принятия управленческого решения является критерий достаточности данных, который зависит от удельного веса ФЛО в общем объеме обработанных документов.
Пусть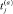 
– момент времени завершения контроля на переделах СОУИ j-го обрабатываемого документа a-го вида страхового учета;
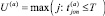– общее количество обработанных страховой СОУИ документов a-го вида страхового учета за отчетный период Tоп.
Введем массивы истинных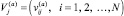 
и реальных 
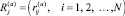статусов j-го обрабатываемого документа на переделах СОУИ для j=1, 2, …, U(a).
Пусть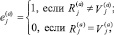 
а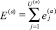
– общее количество документов a-го вида страхового учета, не прошедших форматно-логический контроль за отчетный период Tоп. Тогда задача оценки достоверности информации СОУИ будет иметь вид:
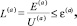
где L (a), ε(a) – реальный и допустимый уровни ошибок выходных данных по a-му виду страхового учета соответственно.
При этом должны выполняться ограничения на:
–количество ФЛО, при котором документ считается не прошедшим контроль (для рассматриваемого случая необходима и достаточна идентификация одной ФЛО на любом переделе объектно-структурной модели СОУИ);
–математическое ожидание Τфло времени идентификации форматно-логических ошибок в СОУИ: τ0≤Τфло≤τN, где τ0, τN – крайние метки времени учетной транзакции.
Постановка задачи оптимизации подсистемы учета бланков строгой отчетности (БСО)
Оборот БСО (страховых полисов и квитанций на оплату) относится к категории обеспечивающих бизнес-процессов операционной деятельности страховой компании и поддерживается подсистемой учета БСО.
Стоит отметить, что учет БСО является показательным для представления специфики организации страхового учета. Для обеспечения поддержки процессов продаж и сопровождения страховых продуктов операции с БСО выполняются в рамках транзакций учета договоров страхования. Соответственно события, инициирующие изменение статусов БСО и договоров страхования, являются пересекающиеся множествами, что необходимо учитывать при формализации постановок задач оптимизации систем страхового учета, обеспечивающих совместную обработку указанных доку ментов (рис.2).
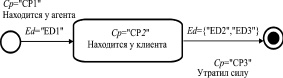
Рис. 2. Пример графа перехода статуса бланка страхового полиса (Сp – код состояния БСО, Ed – код события, инициирующего изменение статусов договора и БСО, где ED1 – заключение договора; ED2, ED3 – переоформление и расторжение договора соответственно)
Вместе с тем учет БСО в отличие от других видов страхового учета организован по балансовой модели. Поэтому для формализации постановки задачи оптимизации подсистемы учета БСО можно использовать следующее выражение:
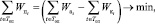
где Wп – потери БСО (например, утраченные и испорченные агентами страховые полисы); Wа – БСО, полученные агентами для заключения договоров страхования; Wк – БСО, переданные клиентам при заключении договоров страхования.
При ограничениях на:
–количество типов используемых БСО;
–количество видов страхования, по которым организован учет БСО.
Параметры ограничений определяются учетной политикой страховой компании.
Постановка задачи оптимизации автоматизированной системы управления (АСУ) андеррайтингом
Целью моделирования является оптимизация АСУ андеррайтингом для рисковых видов страхования.
Будем исходить из того, что бизнес-процесс андеррайтинга является многоэтапным процессом оценки конечного множества факторов риска (этапов) F по договорам определенного вида рискового страхования. Данный процесс можно формализовать в виде ориентированного дерева O(A, A′, D), где А – конечное множество факторов риска, которые андеррайтер может оценить при поддержке АСУ андеррайтингом (A⊂F); A′ – конечное множество факторов риска, принятие решения по которым не поддерживается АСУ андеррайтингом (A′⊂F); D – маршрут процесса андеррайтинга.
Тогда задача функциональной оптимизации АСУ андеррайтингом может быть описана в следующем виде:
|A|→|F|
при ограничении на максимально допустимое время принятия андеррайтером решения по договору, устанавливаемое Правилами по данному виду страхования.
Постановка задачи оптимизации системы электронного документооборота урегулирования убытков
Управление бизнес-процессом урегулирования убытков заключается в сборе и обработке страховых документов, используемых для принятия решения о выплате страхового возмещения. Для реализации данных задач применяются системы электронного документооборота (СЭД) урегулирования убытков.
Математически задача оптимизации N-этапной СЭД урегулирование убытка может быть интерпретирована как задача обхода ориентированного графа ЖЦ выплатного дела за время в днях, не превышающее установленный для данного вида страхования максимальный срок урегулирования убытка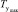 
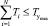
при ограничениях на минимальное и максимальное количество этапов выплатного дела, устанавливаемое Регламентом бизнес-процесса урегулирования убытков для данного вида страхования.
Заключение
Применение предлагаемого в статье подхода к формализации постановок задач функциональной оптимизации специализированных компонентов КИС региональной страховой компании обеспечило повышение эффективности их использования, что в конечном итоге способствовало увеличению финансового результата компании по некоторым рисковым видам страхования на 10 %.