Электромембранные системы, как и любые электрические системы, могут функционировать в различных режимах когда задается скачок потенциала (потенциодинамический или потенциостатический режимы) в системе или плотность тока (гальванодинамический или гальваностатический режимы). Для моделирования переноса в мембранных системах используется система уравнений Нернста ? Планка и Пуассона. Эта система уравнений удобна для моделирования потенциодинамического или потенциостатического режимов, так как уравнение Пуассона используется для вычисления потенциала. Вто же время накоплено большое количество экспериментальных данных именно для гальванодинамического или гальваностатического режимов, которые требуют теоретического анализа. Всвязи с этим возникает проблема вывода уравнений и краевых условий, удобных для моделирования этих режимов. Решению этой проблемы в двумерном нестационарном случае посвящены работы [1, 2, 4]. Вданной работе, являющей продолжением и развитием этих работ и работы [6], рассматривается важный частный случай одномерного нестационарного переноса бинарного электролита, допускающего значительное упрощение по сравнению с двумерным случаем.
Физическая постановка задачи
Электродиализный аппарат имеет периодическую структуру, состоящую из чередующих камер обессоливания и концентрирования, а также двух электродных камер. Число камер, как правило, достаточно большое, достигает нескольких сотен, и поэтому влиянием изменения концентрации в электродных камерах на изменение концентраций в камерах обессоливания и концентрирования пренебрегают. Кроме того, изменение концентрации в камере концентрирования можно учесть в граничных условиях. Таким образом, основной задачей является моделирование переноса в камере обессоливания. Пусть H – ширина камеры обессоливания, соответственно, x=0 – соответствует условной межфазной границе анионообменная мембрана/раствор, x=H – соответствует условной межфазной границе катионообменная мембрана/раствор, t≥0 – время.
Исходная система уравнений
Массоперенос в электромембранных системах описывается электродиффузионными уравнениями [5]. Векторная запись этой системы для бинарного электролита, в случае отсутствия химических реакций, имеет вид
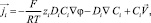i =1, 2; (1)
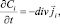i =1, 2; (2)
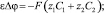(3)
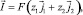(4)
где ∇ – градиент; Δ – оператор Лапласа;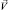 
– скорость течения раствора; ρ0 – характерная плотность раствора; P – давление,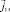 
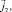C1, C2 – потоки и концентрации катионов и анионов в растворе, соответственно; z1, z2 – зарядовые числа катионов и анионов; 
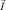– плотность тока; D1, D2 – коэффициенты диффузии катионов и анионов соответственно; φ – потенциал электрического поля; ε – диэлектрическая проницаемость электролита; F – постоянная Фарадея; R – газовая постоянная; T – абсолютная температура; t – время.
Уравнения Нернста – Планка (1) описывают поток растворенных компонентов, обусловленный миграцией в электрическом поле, диффузией и конвекцией; (2) – уравнение материального баланса в точке (малом элементе объема); (3) – уравнение Пуассона для потенциала электрического поля; (4) – плотность тока в растворе электролита, обусловлена движением заряженных компонентов.
Если рассматривать плоскопараллельное течение в канале, то можно считать его двумерным. Рассмотрим некоторое сечение двумерного канала обессоливания. Система уравнений Нернста – Планка и Пуассона в этом сечении упростится, так вектора станут скалярами, а функции будут зависеть от одной переменной x. Сучетом этого, система уравнений (1)–(4) приобретает вид
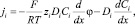i =1, 2; (5)
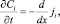i =1, 2; (6)
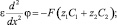(7)
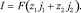(8)
Эта система удобна для моделирования потенциодинамического и потенциостатического режимов, поскольку имеется уравнение (7) для вычисления потенциала, но неудобна для моделирования гальванодинамического и гальваностатического режимов.
Систему уравнений (1)–(4) или (5)–(8) можно записать с использованием не потенциала φ, а напряженности электрического поля E= –∇φ (соответственно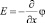 
), тогда уравнения (1), (3) и, соответственно, (5), (7) изменятся. Например, уравнения (5), (7) приобретут вид (9) и (10).
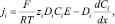i =1, 2; (9)
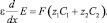(10)
Замечание1. Если подставить уравнения для потоков (1) или (5) или в (2) или (6), то можно исключить потоки и получить уравнения для концентраций.
Вывод системы уравнений для моделирования «гальванического» режима
Для вывода системы уравнений, удобной для моделирования гальванодинамического режима, необходимо заменить:
–формулу для плотности тока на формулу для напряженности электрического поля;
–уравнение Пуассона для потенциала уравнением для плотности тока.
1.Вывод формулы для напряженности электрического поля вместо уравнения для плотности тока
Умножим уравнения (9) на zi и сложим, тогда с учетом формулы (10), получим
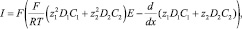
откуда следует, что
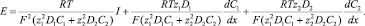
Обозначим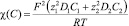 
– проводимость раствора, и, соответственно, 
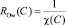– омическое сопротивление раствора, тогда формула для напряженности запишется в виде (см. [5]):
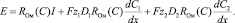(11)
Из формулы (11) следует (см. [5]), что при отсутствии концентрационной поляризации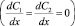 
выполняется закон Ома. Сдругой стороны, даже при отсутствии тока (I=0) концентрационная поляризация (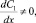
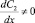) создает электрическое поле.
2.Вывод уравнений для концентраций, не зависящих от E
Подставив (11) в (9), выразим потоки через плотность тока, получим (12) или (13).
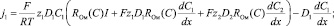(12)
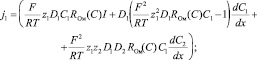(13)
Аналогично
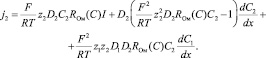(14)
3.Вывод уравнения для плотности тока вместо уравнения Пуассона
Подставим (11) в уравнение Пуассона (10), тогда получим уравнение для плотности тока I:
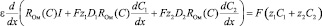
или
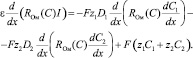(15)
Система уравнений (6), (11), (13)–(15) является замкнутой системой уравнений относительно неизвестных функций C1, C2, j1, j2, I и моделирует гальванодинамический режим. Эта система уравнений является аналогом системы уравнений (5)–(8), используемых для моделирования потенциодинамического режима.
Замечание2. Если вместо неизвестной функции I(t, x) ввести неизвестную функцию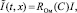 
то система уравнений (6), (11), (13)–(15) несколько упростится.
Замечание3. Исключая потоки, а именно подставляя (13) и (14) в уравнения (6), можно получить уравнения, содержащие только неизвестные функции C1, C2, I.
4.Моделирование гальваностатического режима в стационарном случае
Моделирование гальваностатического режима в стационарном случае значительно упрощается. Действительно, из уравнения (6) следует, что в стационарном случае потоки постоянны, но тогда согласно формуле (8) и плотность тока постоянна (задается). Одним из уравнений для определения потоков является уравнение (8). Вкачестве второго уравнения должно использоваться какое-то граничное условие. Напряженность электрического поля E находится по формуле (11), далее решаем систему уравнений (12) и (14) относительно C1, C2. Стационарный перенос в одномерном случае корректно моделировать в непересекающихся диффузионных слоях возле каждой ионообменной мембраны [3]. Впротивном случае необходимо использовать двумерные модели.
5.Моделирование гальванодинамического режима при выполнении условия электронейтральности
Система уравнений (6), (11), (13)–(15) значительно упрощается при выполнении условия электронейтральности. Однако проще непосредственно получить соответствующие уравнения из уравнений (6), (8), (9), (10).
1.Прежде всего, заметим, что при выполнении условия электронейтральности
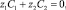(16)
получаем, что плотность тока не зависит от x. Действительно, умножим уравнения (6) на zi и сложим, тогда получим
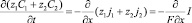
или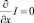 
, т.е.I= I(t).
Кроме того, из (16) следует, что
z1C1= –z2C2=C,
где C – эквивалентная концентрация. Используя вместо парциальных концентраций эквивалентную концентрацию, можно упростить уравнения. Выразим через эквивалентную концентрацию все формулы и уравнения.
2.Вычислим
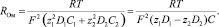
3.Упростим формулу (11)
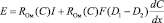
или
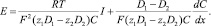(17)
4.Вычислим потоки. Для этого можно использовать (12), (14). Однако это проще сделать непосредственно из уравнения (9).
Выразим потоки через эквивалентную концентрацию:
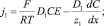(18)
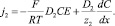(19)
5. Вывод уравнения для эквивалентной концентрации
Умножим первое уравнение (6) на D2, а второе уравнение на D1 и сложим их, тогда получим
или
Переходя в левой части к эквивалентной концентрации, а в правой воспользовавшись формулами (18), (19), получим
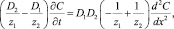
или
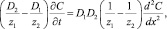
или
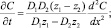
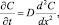(20)
где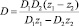 
– коэффициент диффузии раствора электролита.
Таким образом, по заданной плотности тока I(t) остальные характеристики процесса вычисляются следующим образом:
а)решается краевая задача для уравнения (20) и находится эквивалентная концентрация C и, соответственно, парциальные концентрации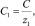 
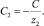
б)напряженность электрического поля рассчитывается по формуле (17).
Заключение
Вработе из системы уравнений Нернста – Планка и Пуассона выведены уравнения, моделирующие перенос ионов соли в гальванодинамическом режиме для одномерного случая. Рассмотрены также частные случаи стационарного переноса и выполнения условия локальной электронейтральности.
Исследование выполнено при финансовой поддержке РФФИ в рамках научных проектов №13-08-93105-НЦНИЛ_а и 13-08-96525 р_юг_а.