Снижение материалоемкости и стоимости конструкций при условии их надежности и долговечности является важнейшей задачей повышения эффективности строительного производства. На строительных объектах нефтегазовых комплексов, химической промышленности применяются многослойные пластины и оболочки. Слои таких конструкций соединяются между собой связями, которые допускают проскальзывание одного слоя по отношению к другому. Такие системы обладают высокой прочностью и жесткостью при относительно малой массе, хорошими тепло- и звукоизоляционными свойствами и, следовательно, экономической эффективностью. Вопрос оптимального проектирования таких конструкций является актуальным.
Цель исследования – разработка методики расчета составных конструкций на оптимальность с позиции снижения стоимости при соблюдении всех прочностных и технологических требований.
Задачей оптимизации составных пологих оболочек со слоями переменной толщины является отыскание экстремума целевой функции в заданной области проектирования при условии выполнения установленных ограничений.
Fc = F(X, U) ? min, (1)
где Fc – функция цели; X = {x1, ..., xn} – параметры проектирования; U = {u1(t), ..., un(t)} – функции проектирования; t – пространственные координаты.
Пространственными координатами являются геометрические размеры оболочки, функции проектирования определяют форму оболочки. В качестве функции цели могут быть представлены: минимум веса (стоимости), максимум нагрузки и другие критерии оптимальности. Существенным элементом постановки задачи является выбор основных определяющих уравнений. В данной задаче используется предлагаемая математическая модель для такого типа конструкций [4].
Выбор критерия оптимальности и системы ограничений определяется назначением и условиями работы составной оболочки. В качестве критерия оптимальности выбирается стоимость конструкции. Ограничения представлены в виде системы неравенств:
?i(x) ? 0 (i = 1, ..., m1);
Gj(x) ? 0 (j = 1, ..., m2), (2)
где ?i, Gj – заданные функции параметров проектирования.
Ограничения (равнопрочность, устойчивость и т.д.) [5], при условии выполнения которых оптимизируется функция цели, устанавливаются конкретно для каждой конструкции.
При оптимизации составных пологих оболочек со слоями переменной толщины с дискретным соединением слоев осуществляется определение следующих независимых параметров: начальная толщина слоя на границах 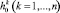 , амплитуда изменения толщин слоев
, амплитуда изменения толщин слоев 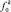 при заданном законе изменения толщины, диаметр анкерного элемента d, модуль упругости материала E, в который внедрены анкера, а также шаг анкеровки hx, hy в направлениях х и у соответственно.
при заданном законе изменения толщины, диаметр анкерного элемента d, модуль упругости материала E, в который внедрены анкера, а также шаг анкеровки hx, hy в направлениях х и у соответственно.
Здесь рассматривается прямая задача оптимизации, где отыскание оптимальных параметров осуществляется при заданных функциях проектирования. Общая схема алгоритма представлена на рис. 1.

Рис. 1. Алгоритм оптимизации составных конструкций
В соответствии с разработанным алгоритмом задаются параметры исследуемой конструкции в установленном интервале, определяется напряженно-деформированное состояние, проверяются условия равнопрочности, устойчивости сжатого слоя, прочность дискретных связей. Если условия не выполняются, снова задается новое сочетание параметров и цикл повторяется. Далее определяется стоимость материала конструкции при заданном количестве вариантов с оптимальными параметрами и выбирается минимальное значение.
По описанию математической модели (1) и (2) задача оптимизации составной пологой оболочки относится к задаче нелинейного математического программирования. Кроме того, задача является сложной в связи с многопараметричностью.
Её реализация осуществляется методом случайного поиска в форме, разработанной Ю.А. Сушковым [3]. Преимущество данного метода по сравнению с другими методами математического программирования заключается в том, что при реализации метода случайного поиска не требуется непрерывности целевой функции и наличия производных. Для рассматриваемой задачи оптимизация применения методов, использующих производные, является очень сложной, так как трудно получить производные в виде аналитических функций при большом количестве переменных. Суть метода заключается в том, что с помощью датчика псевдослучайных величин (дает числа от нуля до единицы с равномерной плотностью распределения) по специальному алгоритму выбираются искомые параметры (интервал поиска задан, здесь используются геометрические ограничения). Затем определяется функция, составленная из условия равнопрочности конструкции, и за L-е количество шагов определяются оптимальные параметры и далее стоимость конструкции. Затем расчет повторяется необходимое количество раз. Из полученных результатов стоимости выбирается минимальное её значение.
Процесс поиска разбивается на ряд этапов [3]. В свою очередь, каждый этап состоит из mL шагов (L – номер этапа). Общим для всех алгоритмов случайного поиска является применение в процессе оптимизации случайных чисел, из которых наиболее удобны псевдослучайные (квазислучайные) последовательности. То есть на каждом шаге вырабатываются случайные числа ?k, имеющие ступенчатую плотность распределения (рис. 2). Параметры HH и HQ зависят от номера этапа L таким образом, что HHL+1 > HHL и QL+1 < QL и на каждом этапе пересчитываются по следующим выражениям [3]:
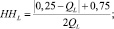 (3)
(3)
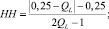 (4)
(4)
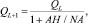 (5)
(5)
где AH – коэффициент сжимаемости; NA – количество искомых параметров.
Среднее значение ?ср – соответствует текущему минимальному значению функции цели F. Датчик псевдослучайных величин дает числа (ak) от нуля до единицы. Эти величины в соответствии со ступенчатой плотностью распределения (рис. 2) трансформируются по следующим соотношениям:
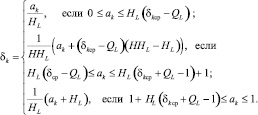 (6)
(6)
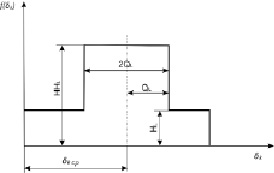
Рис. 2. Плотность распределения случайных величин
Задавшись интервалом поиска xk min и xk max, устанавливается связь между искомыми параметрами xk и случайными числами
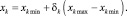 (7)
(7)
Значение функции цели F на mL шаге подсчитывается по найденным значениям xk и сравнивается с предыдущими. Если значение F больше минимального, которое было получено за все предыдущие шаги, то происходит переход к следующему шагу. В противном случае вместо старого значения текущего минимума запоминается вновь полученное и набор параметров, при котором она получена. После выполнения каждого этапа закон, по которому выбирается значение параметров xk (рис. 2), изменяется таким образом, чтобы вероятность попасть в окрестность глобального минимума увеличилась бы. При этом используется часть информации, полученной на предыдущих шагах. Процесс расчета продолжается, пока QL не станет меньше заданной точности ?. При решении технических задач оптимального проектирования принимается ? = 0,005 – 0,015. Для определения коэффициента сжимаемости AH рекомендуется использовать эмпирическую зависимость
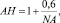
где NA – число оптимизируемых параметров [2].
Достоверность численных результатов обосновывалась на тестовой задаче. Была рассмотрена составная пологая оболочка со слоями переменной толщины, шарнирно опертая по контуру, загруженная равномерно распределенной нагрузкой с конкретно заданными параметрами. Определено ее напряженное состояние. Полученные максимальные значения напряжений были приняты в качестве допускаемых.
В качестве примера в работе рассматривалась трехслойная оболочка, шарнирно опертая по контуру. Материал слоев изотропный, упругий с линейными механическими характеристиками.
Напряженно-деформированное состояние конструкции определялось в соответствии с разработанной математической моделью [4, 5]. Верхний и нижний слои постоянной толщины. Средний слой имеет переменную толщину.
В соответствии с алгоритмом оптимизации (рис. 1) осуществлялось варьирование независимыми параметрами. При численной реализации представленной здесь задачи количество таких параметров равнялось двум. Это толщина верхнего листа (h(1)) и амплитуда изменения толщины среднего слоя 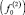 . Для каждого из них был задан интервал поиска: 0,1 ? h(1) ? 30 мм;
. Для каждого из них был задан интервал поиска: 0,1 ? h(1) ? 30 мм; 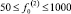 мм. Выбор оптимальных геометрических параметров h(1),
мм. Выбор оптимальных геометрических параметров h(1), 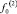 проводился при фиксированном количестве анкерных связей. При этом для каждого определенного количества анкеров проводилась серия расчетов с заданными интервалами поиска для всех варьируемых здесь параметров. Остальные параметры рассчитываемой оболочки фиксировались: h(3) = 2h(1) ; диаметр анкера d = 18 мм;
проводился при фиксированном количестве анкерных связей. При этом для каждого определенного количества анкеров проводилась серия расчетов с заданными интервалами поиска для всех варьируемых здесь параметров. Остальные параметры рассчитываемой оболочки фиксировались: h(3) = 2h(1) ; диаметр анкера d = 18 мм; 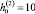 мм;
мм;
E(2) = Eб = 0,34?104 МПа [1].
Размеры оболочки в плане а = 5000 мм, b = 6000 мм. Верхний и нижний слои стальные,
E(1) = 2,1?105 МПа, v(1) = 0,3.
Средний слой – бетон, v(2) = 0,2. Оболочка рассчитывалась при равномерно распределенной нагрузке интенсивностью 0,025–0,05 МПа.
Ограничения:
1. Условие равнопрочности
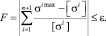
Здесь ?i max – максимальные напряжения, МПа; [?i] – допускаемые напряжения, МПа.
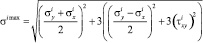 ,
,
где 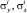 – нормальные напряжения в i-м слое в направлениях x и y соответственно, МПа;
– нормальные напряжения в i-м слое в направлениях x и y соответственно, МПа;  – касательные напряжения в i-м слое, МПа; ? = 10 %.
– касательные напряжения в i-м слое, МПа; ? = 10 %.
2. Геометрические ограничения учтены при выборе интервала поиска оптимальных параметров.
На рис. 3 представлены графики расчетов составной пологой оболочки при различных величинах нагрузок и различных жесткостях связей между слоями.
Звездочкой (?)показан оптимальный вариант, соответствующий минимальной стоимости конструкции.
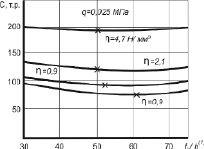
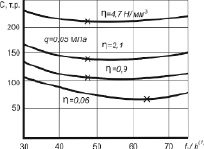
Рис. 3. Выбор минимальной стоимости: q – величина равномерно распределенной нагрузки по поверхности оболочки; h – коэффициент жесткости связей между слоями
Выводы
Разработана методика расчета составных конструкций на оптимальность с позиции снижения их стоимости при соблюдении всех прочностных и технологических требований.
Определены оптимальные варианты стоимости составных оболочек при различных нагрузках и жесткостях межслойных связей.



