Разработка определения тенденций изменения значений характеристик объектов управления сложных систем (ОУСС) с учетом динамики характеристик систем алгоритма позволит: проводить анализ характеристик ОУСС в момент принятия решения; определить закономерности их изменения во времени и определить их возможные значения для следующего временного периода, предполагая, что стратегия принятия управленческих решений не будет изменяться. Лицо, принимающее решения (ЛПР), на основе прогноза принимает корректирующее решение о стратегии принимаемых управленческих решений.
ЛПР при формировании управленческих решений для ОУСС необходимо анализировать характеристики в динамике и строить временной ряд. Моделирование ОУСС с динамическими характеристиками целесообразно проводить на основе временных рядов, которые являются дискретной последовательностью наблюдений, производимых через требуемые промежутки времени. Основная задача моделирования ОУСС с помощью временных рядов [1, 2] заключается в создании моделей, обладающих максимальной простотой и минимальным числом параметров, но при этом адекватно описывающих функционирование этой системы.
Разработка такого типа моделей обеспечит оптимальное прогнозирование функционирования ОУСС, которое может быть использовано для выработки стратегии оптимального управления ЛПР. На основе выработки этой стратегии ЛПР становится ясно, каким образом целесообразно регулировать переменную для того, чтобы обеспечить минимизацию возмущения некоторой зависимой переменной.
Определение ЛПР оптимального прогнозирования, динамических взаимосвязей параметров и оптимального управления ОУСС имеет большое практическое значение при принятии управленческих решений. Такие вероятностные модели могут быть стационарными и нестационарными. Стационарные модели описывают функционирование ОУСС, процессы, в котором остаются равновесными относительно среднего уровня. Нестационарные модели описывают функционирование ОУСС, в котором процессы не имеют естественного среднего значения.
Стохастическая модель, прогнозирование которой описывается характеристиками экспоненциально взвешенного скользящего среднего являются оптимальными, нестационарными процессами и относятся к процессам авторегрессии проинтегрированного скользящего среднего (АРПСС). Определив класс моделей, можно разрабатывать конкретную модель предметной области в установлении соответствия выбранного класса моделей АРПСС имеющимся данным. Для установления соответствия выбранного класса моделей АРПСС имеющимся данным используются методы идентификации на основе корреляционных и частных автокорреляционных функций. Идентифицированная модель описывается временным рядом при помощи функции правдоподобия, которая позволит оценить максимально правдоподобно параметры ОУСС, в другом случае требуется использовать байесовское апостериорное распределение.
Первоначально выбранная модель не обязательно адекватно описывает функционирование ОУСС. Для определения адекватности модели необходимо проводить диагностическую проверку в том случае если выбранная модель неадекватна необходимо выбрать подходящие изменения на основе одного или нескольких итеративных циклов идентификации, подгонки и диагностической проверки. Прогноз, проводимый на основе моделей с использованием временного ряда, для выработки оптимального прогнозирования производится при помощи простых рекуррентных вычислений. Найденная модель определяет, будут ли прогнозированные параметры изменяться линейно, экспоненциально и т.д. с точной оценкой, как при прогнозе используются данные из прошлого, определить дисперсию ошибок прогноза и вычислить пределы, в которых с заданной точностью будут лежать будущие значения ряда.
Для моделирования процесса прогнозирования значений параметров ОУСС используем метод, основанный на определении авторегрессионной зависимости. В этом случае все значения параметров группируются по соответствующим временным периодам. Как правило, значение временного интервала регрессии определяется календарным периодом. Значения параметров в каждом интервале усредняются по каждому параметру. Усредненные значения параметров объединяются в интегрированное значение с определением коэффициентов значимости объединенной характеристики и формируются ЛПР на основе экспертных оценок. Процесс прогнозирования значений параметров ОУСС (на примере вуза) можно представить следующей схемой (рисунок).
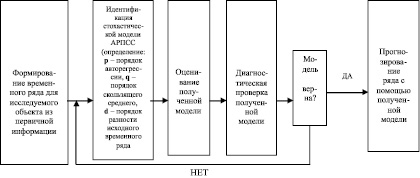
Процесс прогнозирования значений параметров ОУСС
Представим базовую информацию, циркулирующую в ОУСС, в виде множества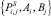 
, где 
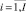– индекс ОУСС, носителя первичной информации (например, учащийся, учебная группа, курс и т.д.); 
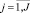– индекс выбранных или всех характеристик объектов управления (например, изучаемые в вузах предметы); 
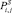– количественное значение j-й характеристики i-го объекта (например, полученная на занятии оценка, код вида пропуска занятия и т.п.); S – дата формирования Pi,j; Ai – наименование i-го объекта; Вj – наименование j-й характеристики.
Для решения поставленной задачи на текущий момент времени формируется на основании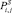 
по i-му объекту управления для всех характеристик временной ряд 
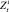следующим образом:
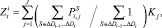
где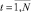 
, порядковые номера временных интервалов длиной в 7 дней от DN до DK; DN – дата начала исследуемого периода; DK – дата окончания исследуемого периода;
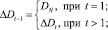
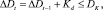
где Kd – количество дней в периоде формируемого ряда; Kj – веса значимости j-й характеристики. Прогнозирование будет вестись по каждому объекту. Для этого нужно для каждого i-го объекта выделить его временной ряд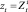 
с числом членов равным N и выполнить пункты I, II, III, IV, V.
I. Идентификация стохастической модели
Методы идентификации – это процедуры, применяемые к исходному временному ряду для вычисления типа моделей значений характеристик, которые имеет смысл использовать в дальнейшем. Конкретная цель состоит в том, чтобы получить некоторое указание на то, какие значения р (порядок авторегрессии), q (порядок скользящего среднего) и d (порядок разности исходного временного ряда) нужны в общей линейной модели прогресса авторегрессии проинтегрированного скользящего среднего (АРПСС), и выбрать некоторые начальные значения параметров. Полученная пробная модель является отправной точкой для применения более формальных и эффективных методов оценивания. Подход к идентификации состоит в следующем. Берется конечная разность от исходного временного ряда столько раз, сколько необходимо, чтобы свести процесс к АРПСС. Идентифицируется результирующий процесс АРПСС. Основной инструмент для реализации (а) и (б) – автокорреляционная и частная автокорреляционная функция. Они используются не только, чтобы облегчить выявление вида модели, но также для получения приближенных оценок параметров.
Исходя из выше определенного, имеем: zt – исходный временной ряд;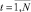 
– индекс по членам исходного временного ряда. Порядок взятия несезонных разностей ряда ztпервоначально принимается d = 0.
1. Вычисление разностного ряда Wt.
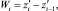
где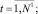 
N1 = N – d;
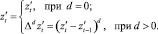
2. Вычисление среднего значения разности ряда
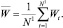
3. Вычисление дисперсии разности ряда
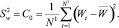
4. Вычисление автоковариационной функции.
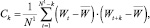
где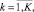 
K = N1/4.
5. Вычисление автокорреляционной функции
rk = Ck/C0.
6. Определение тенденции к затуханию у автокорреляционной функции [2, 3]. ?rk = rk – rk–1. Если ?rk = rk – rk–1 убывает, то автокорреляционная функция имеет тенденцию к затуханию, поэтому получен нужный d и переход к следующему пункту, иначе d = d + 1 и переход к пункту 1.
7. Вычисление частной автокорреляционной функции.
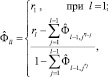при l = 2, ..., L,
где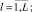 
L = N1/4;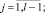 
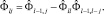
8. Присваивается: p = 1, q = 1.
9. Вычисление оценок параметров авторегрессии 
.
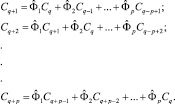
Параметры прогрессии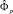 
вычисляют методом подстановки, решив р линейных уравнений [4].
10. Оценка параметров скользящего среднего 
10.1. По известным автоковариациям Ck ряда Wt вычисление модифицированной последовательности ковариации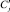 
.
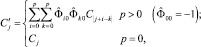
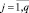
10.2. Вычисление оценок параметров скользящего среднего при помощи квадратически сходящегося процесса алгоритма Ньютона – Рафсона
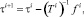
где i – очередной шаг итерации (первоначально i = 0);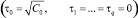 
– начальные значения;
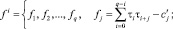
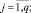
10.3. Проверяется условие окончания итеративного процесса. Если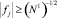 
, то переход к пункту 10.2 на следующую итерацию, иначе итеративная процедура считается завершенной.
10.4. Вычисление величин по последнему значению ? из пункта 10.2. Оценки параметров скользящего среднего
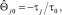где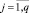 
.
Оценка общей константы
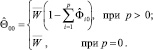
Оценка дисперсии белого шума
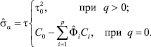
II. Оценивание модели
Целью оценивания является подгонка выбранной модели к исходным данным для получения эффективной оценки параметров. Для этого используется метод максимального правдоподобия, реализованный оценками наименьших квадратов [5].
1. Прогнозирование назад ряда Wt.
1.1. Вычисление по возвратной рекуррентной формуле
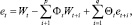
где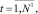 
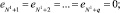
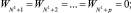
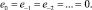
1.2. Вычисление по возвратной рекуррентной формуле W0, W–1, …, W–b, используя полученное e1, до затухания W
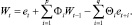
2. Вычисление остаточных ошибок at рекуррентным расчетом вперед
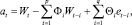N1
где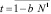 
.
3. Вычисление безусловной суммы квадратов остаточных ошибок
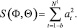
4. Вычисление оценок наименьших квадратов. Вычисление параметров, минимизирующих сумму квадратов остаточных ошибок, производится методом оптимизации с ограничениями, предложенным Марквардтом.
Обозначим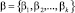 
все параметры модели, т.е. 
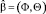. Присвоим 
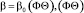– полученные выше ограниченные параметры; ? = 0,01; F2 = 2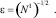 
4.1. Вычисление производных по ранее полученным остаточным ошибкам.
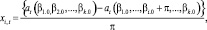
где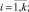 
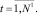
4.2. Вычисление по известным at, xi,t следующих величин: – матрица размером k?k A = {Aij}, где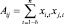 
– вектор g с элементами g1, g2, …, gk, где 
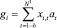– нормирующие величины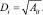 
4.3. Вычисление модифицированных (введением нормирующих множителей и наложением ограничений) лианезированных уравнений.
A*h* = g*,
где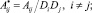 
i ? j
Aij = 1 + ?;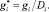 
Уравнения решаются относительно h*. Этот вектор деноминируется для получения поправок параметров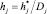 
.
4.4. Вычисление новых значений параметров ? = ?0 + h.
4.5. Вычисление суммы квадратов остаточных ошибок S(?).
4.6. Проверка окончания итерации:
– если все S(?) – S(?0) ? ?, то сходимость и переход к следующему пункту;
– если не все S(?) – S(?0) ? ?, то ?0 = ?,? уменьшается в F2 раз и переход на 4.2;
– если S(?) > S(?0), то ?увеличивается в F2 раз и переход на пункт 4.1.
5. Вычисление стандартных ошибок и корелляционной матрицы.
5.1. Оценка остаточной дисперсии по полученной на последней итерации суммы квадратов S(?)
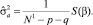
5.2. Вычисление ковариационной матрицы оценок
где Х – регрессионная матрица в лианезированной модели, вычисленная на последней итерации в процедуре Маквардта.
5.3. Вычисление стандартных ошибок
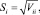
где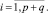 
5.4. Вычисление корреляционной матрицы
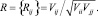
6. Вычисление общей константы
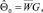
где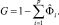 
III. Диагностическая проверка модели
1. Вычисление остаточных автокорреляций по остаточным ошибкам ai соответствующим оценкам наименьших квадратов
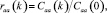
где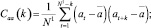 
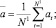
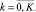
2. Вычисление статистики
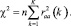
3. Проверка модели.
Если вычисленная статистика х2 совпадает с табличной статистикой X2 с V = K–p – q степенями свободы и заданным уровнем вероятности, то значит модель идентифицирована и подогнана верно, если нет – то итеративно изменить параметры модели р и q и перейти к пункту 1.9 [10, 7].
IV. Прогнозирование с помощью подобранной стохастической модели
1. Вычисление прогноза в момент времени t на l шагов вперед
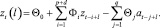
2. Вычисление верхних и нижних пределов прогноза
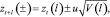
где u = 0,68; 1,65; 1,96; 2,58 в зависимости от того, лежит ли вычисленное значение между этими пределами с вероятностью 0,50; 0,90; 0,95; 0,99 соответственно [7, 8];
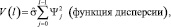
где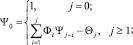 
; 
.
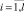V. Исследование полученных результатов
Если полученный прогноз zt(l) < OЭ, (ОЭ – пороговое значение, сформированное ЛПР), тогда информация по i-му объекту, используя идентификационный вектор Ai, выводит на печать для последующего анализа и принятия управленческого решения [9, 6].