В статье рассматриваются процессы переноса в одно- и двухфазных средах в стационарных насадочных и зернистых слоях с хаотичной засыпкой при турбулентном режиме движения газов и жидкостей сквозь слой. Такие слои широко используются для проведения как гидромеханических процессов (например, проточные статические смесители, насыпные фильтры), так и тепломассообменных и реакционных процессов. Сюда относятся некоторые процессы гетерогенного катализа, сушка в слое, нагревание материала в шахматных и доменных печах, адсорбция, абсорбция, ректификация и т.п. [1, 5, 14, 16].
Ниже показано применение моделей пограничного слоя для получения расчетных выражений средних коэффициентов тепло- и массоотдачи и их использование для расчета эффективности тепло- и массопереноса в каналах и аппаратах с насадками при турбулентном режиме (Reэ > 50) [14].
Касательное напряжение в насадочном слое
Важной характеристикой при движении потоков является касательное напряжение на стенках каналов и на других элементах аппаратов. От касательного напряжения зависят затраты на перекачку газов и жидкостей, а также его значение часто используется в различных моделях для расчета коэффициентов тепло- и массоотдачи.
Среднее касательное напряжение на стенке τст находят, используя уравнение баланса сил, а если это затруднительно, то выражают через среднюю объемную или массовую скорость диссипации энергии в аппарате [4, 6, 7]. Например, для неупорядоченного насадочного или зернистого слоя такое выражение имеет вид [7, 8]
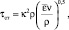 (1)
(1)
где κ – коэффициент пропорциональности; ρ – плотность фазы кг/м3;  – средняя скорость диссипации энергии, Вт/м3; ν – коэффициент молекулярной вязкости, м2/с. Среднюю скорость диссипации энергии
– средняя скорость диссипации энергии, Вт/м3; ν – коэффициент молекулярной вязкости, м2/с. Среднюю скорость диссипации энергии  можно выразить через фиктивную скорость среды w0 в полном сечении аппарата без насадки
можно выразить через фиктивную скорость среды w0 в полном сечении аппарата без насадки
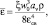 (2)
(2)
где ξ – коэффициент гидравлического сопротивления; aν – удельная поверхность насадки, м2/м3; εсв – удельный свободный объем насадки; w0 – средняя скорость, м/с.
Или через среднюю истинную скорость среды 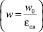
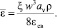 (3)
(3)
Используя эквивалентный диаметр насадки 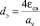 из (3), можно получить
из (3), можно получить
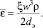 (4)
(4)
Выражение (2) следует из зависимости для средней диссипации энергии
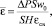 (5)
(5)
где ΔP – перепад давления, Па; S – площадь сечения аппарата, м2.
В числителе стоит диссипируемая энергия, а в знаменателе свободный объем насадки, т.е. объем, занятый газом или жидкостью.
В теории пограничного слоя широко используется понятие динамической скорости
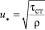 .
.
Из выражений (1) и (4) запишем среднюю динамическую скорость для насадочного слоя, т.е. на поверхности элементов
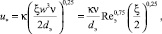 (6)
(6)
где Re – число Рейнольдса 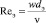 .
.
В работах [7, 8] при турбулентном режиме движения среды (Reэ > 40) для насадок установлен коэффициент пропорциональности в интервале 1,7–2,0. Возьмем среднее значение κ = 1,85.
Модели тепло- и массоотдачи
Для определения средних коэффициентов тепло- и массоотдачи используются модели пограничного слоя в одномерной постановке с применением различных функций турбулентного обмена [6–9]. Записывается сопротивление переносу тепла и массы компонента поперек пограничного слоя в виде
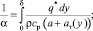
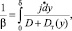 (7)
(7)
где α – коэффициент теплоотдачи, Вт/(м2∙К); β – коэффициент массоотдачи, м/с; δ – толщина пограничного слоя, м; a, D – коэффициенты молекулярного переноса тепла и массы (диффузии), м2/с; aт, Dт – коэффициенты турбулентного переноса тепла и массы, м2/с; y – поперечная координата в пограничном слое, м; ρ – плотность среды, кг/м3; cp – удельная теплоемкость среды, Дж/(кг/К).
Например, из выражения (7) с использованием функций турбулентной вязкости Г.А. Дрейцера, Deissler и др. получены формулы [10]:
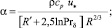 (8)
(8)
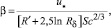 (9)
(9)
где значение R′ для плоского пограничного слоя без возмущения R′ = 5,303; Rδ – безразмерная толщина пограничного слоя; Sc – число Шмидта Sc = ν/D; Pr – число Прандтля, 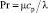 .
.
Значение R′ фактически является одним из пределов интегрирования в формулах (7) и близко к значению безразмерной толщины вязкого подслоя в трехслойной модели (~5). При наличии возмущений это значение будет отличаться от пяти. Такими возмущениями являются кривизна и шероховатость поверхности, сужение и расширения потока в насадочном слое. Для коррекции параметров пограничного слоя, который отличается от плоского, в работах [6–11] используется консервативность его законов к возмущениям (подход С.С. Кутателадзе, А.И. Леонтьева и др.).
С использованием данного подхода, выполняя аналогичный вывод [8] для насадки, получим
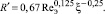 (10)
(10)
Формула для расчета среднего значения Rδ для насадки имеет вид [8]
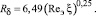 (11)
(11)
Записывая динамическую скорость в виде (6) из формул (8) и (9) с параметрами (10), (11) получим
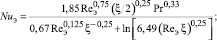 (12)
(12)
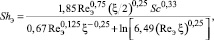 (13)
(13)
где 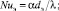
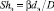 – числа Нуссельта и Шервуда.
– числа Нуссельта и Шервуда.
Расчеты по выражениям (12), (13) дают удовлетворительное согласование с экспериментальными данными и с уравнениями, полученными с применением моделей Прандтля и Кармана [8].
Результаты расчетов
Для проверки полученных выражений (12)–(13) используем как известные критериальные выражения, так и экспериментальные данные различных авторов в виде графиков.
Массоотдачу в газовой фазе от насадочного слоя изучали путем возгонки твердых тел (нафталина) и испарения воды с поверхности пористых тел [1, 14]. Экспериментальные данные обобщены критериальным выражением
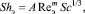 (14)
(14)
где по данным Гильденблата А = 0,407, m = 0,655 (Reэ = 40–104); по данным Аэрова и Умника А = 0,395, m = 0,64 (Reэ = 30–2000) и по данным Шулмена А = 0,45, m = 0,64 (при Reэ = 40–3000).
В работе [11] получена приближенная обобщающая зависимость
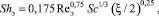 (15)
(15)
а в работе [12] в результате обобщения гидродинамической аналогии Чилтона – Кольборна на градиентные потоки получено
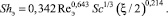 (16)
(16)
Результаты расчетов по формуле (13) удовлетворительно (±15 %) согласуются с результатами, полученными по уравнениям (14)–(16) для различных насадок при 50 < Reэ < 104.
На рис. 1 представлены результаты расчета по формуле (13) и экспериментальные данные, обобщенные в работе [14]. Кольца 25 и 50 мм. Возгонка нафталина.
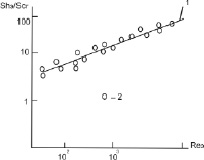
Рис. 1. Корреляция данных по массоотдаче в газовой фазе насадочных колонн: 1 – расчет по уравнению (13); 2 – эксперимент [14]
На рис. 2 дано сравнение по числу Нуссельта при теплоотдаче в нерегулярном насадочном слое из цилиндров и параллелепипедов (ξ = 11,6/Re0,25) с опытными данными для воздуха [2].
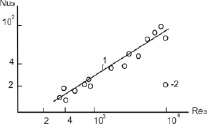
Рис. 2. Теплоотдача в слоях насадочных элементов: 1 – расчет по уравнению (12); 2 – опытные данные [2]
Итак, в результате проведенных исследований моделей пограничного слоя показана принципиальная возможность в их использовании и для расчета теплоотдачи в хаотичных насадках при турбулентном движении однофазных потоков.
Двухфазные потоки в насадках
Рассмотрим применение приведенных выражений для расчета коэффициентов массоотдачи в орошаемых насадках при противоточном пленочном режиме с газовым потоком. До начала подвисания жидкости есть рекомендации производить расчет Shг по уравнениям для сухих насадок. Действительно, поправка Шульмана на орошение при пленочном режиме близка к единице [15].
В работе [3] получены опытные данные по гидравлическому сопротивлению и массоотдаче в газовой фазе для регулярной металлической рулонной насадки. Насадка образована сдвоением металлическими лентами, одна из которых имеет гофры треугольной формы. На боковых поверхностях гофр выполнены лепестки в виде круговых сегментов, при этом хорды сегментов гофр расположены под углом друг к другу. Свободный объем насадки εсв = 0,95, удельная поверхность av = 480 м2/м3, эквивалентный диаметр dэ = 0,0079 м. Опыты проводились при скорости воздуха 0,5 до 3,0 м/с и плотности орошения от 5 до 30 м3/(м2∙ч).
В результате обобщения опытных данных получены коэффициенты сопротивления сухой ξо и орошаемой насадки ξор в виде
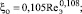 (17)
(17)
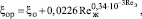 (18)
(18)
где 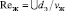 – число Рейнольдса жидкой фазы;
– число Рейнольдса жидкой фазы;  – плотность орошения, м3/(м2∙с).
– плотность орошения, м3/(м2∙с).
Коэффициент массоотдачи в газовой фазе находился экспериментально при увлажнении воздуха водой (Scг = 0,7). На рис. 3 представлены результаты расчетов коэффициента массоотдачи 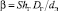 по формуле (13) и опытные данные [3].
по формуле (13) и опытные данные [3].
Согласование с расхождением в пределах погрешности эксперимента
Если при расчете насадочных колонн используется объемный коэффициент массоотдачи, то запишем
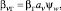 (19)
(19)
где ψw – коэффициент смачиваемости поверхности насадки.
Структуру потока газовой фазы можно оценить по числу Пекле по перемешиванию [13]
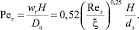 (20)
(20)
Для рассмотренной насадки при wг = 0,5 м/с; Reэ = 263,3; ξ = 0,19 и H = 1,0 м по формуле (20) получаем Рег = 401,6, что указывает на практически идеальное вытеснение потока.
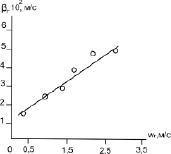
Рис. 3. Зависимость коэффициентов массоотдачи в газовой фазе от скорости газа при плотности орошения 10 (м3/м2∙ч), dэ = 0,0079, м.  – эксперимент [3], линия – расчет по (13)
– эксперимент [3], линия – расчет по (13)
Тогда эффективность массоотдачи в газовой фазе запишем по известному выражению
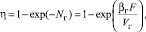 (21)
(21)
где N – число единиц переноса; F = avψvSкH – поверхность контакта фаз, м2; Vг = wгSк – объемный расход, м2/с; Sк – площадь поперечного сечения колонны, м2.
В результате имеем
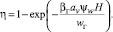 (22)
(22)
Для рассмотренного выше примера при wг = 0,5 м/с получаем η = 0,999, т.е. данная насадка обеспечивает высокую эффективность разделения исследованной смеси.
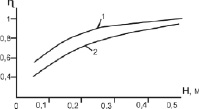
Рис. 4. Зависимость эффективности массоотдачи насадки из колец Рашига от высоты слоя: 1 – Reэ = 100; 2 – Reэ = 500 (Scг = 1)
На рис. 4. даны результаты расчетов эффективности массоотдачи в насадочном слое из колец Рашига размером 50×50 мм (av = 110 м2/м3; εсв = 0,95).
Заключение
На основе выполненных исследований показана возможность использования моделей плоского турбулентного пограничного слоя, с соответствующей корректировкой параметров, для расчета коэффициентов переноса в хаотичных и регулярных насадочных слоях. Основными параметрами полученных уравнений являются число Рейнольдса и коэффициент гидравлического сопротивления слоя. Показаны расчетные и экспериментальные данные для различных типовых насадок. При условии идеального вытеснения потока приведена формула и дан расчет эффективности массопереносса в хаотичной насадке. Полученные уравнения применяются при проектировании или модернизации различного оборудования с насадочными слоями [16].
Статья выполнена в рамках проектной части государственного задания в сфере научной деятельности. Задание № 13.405.2014/К.
Рецензенты:
Зиятдинов Н.Н., д.т.н., профессор, заведующий кафедрой «Системотехника», ФГБОУ ВПО «Казанский национальный исследовательский технологический университет», г. Казань;
Ваньков Ю.В., д.т.н., профессор, заведующий кафедрой «Промышленная теплоэнергетика и системы теплоснабжения», ФГБОУ ВПО «Казанский государственный энергетический университет», г. Казань.



