При эксплуатации гидроузлов возникают экологические проблемы, связанные с образованием воронки размыва в нижнем бьефе при значительных скоростях сбрасываемого потока. Размыв русла в нижнем бьефе может привести к потере устойчивости гидротехнических сооружений. Разработка оценки устойчивости гидроузлов осложняется отсутствием комплексного подхода к анализу русловых процессов, согласованному с теорией плоских гидравлических струй [1]. Основными факторами, влияющими на интенсивность размыва нижнего бьефа гидротехнического сооружения, являются кинематические характеристики потока, сливаемого с концевых сооружений флютбета в незащищенную часть водоотводящего русла.
Целью исследования является определение поля скоростей на основе вихревой модели границы потока, формируемого при сопряжении бьефов гидроузла.
При установленном законе границы струи в результате применения методов аналитической геометрии производится преобразование координат радиуса-вектора точки жидкости из локальной системы, связанной с вихрями, катящимися вдоль границы потока, в декартову прямоугольную систему координат, связанную с границей области размыва, устанавливается закон распределения скоростей.
Математическое моделирование
Преобразуем вектор 
из ортогональной системы локальных координат 
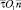в точке O1(x, y) на плоской кривой 
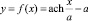в декартову xOy через систему промежуточных координат x1O1y1 (рис. 1).
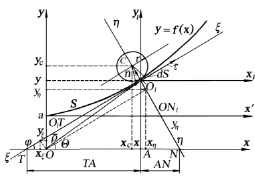
Рис. 1. Преобразование системы локальных ортогональных координат, связанных с касательной и нормалью к кривой, в прямоугольную декартову систему координат
Дифференциально-геометрические характеристики плоской кривой y = f(x) включают ее кривизну k и радиус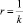 
, дифференциал длины дуги 
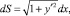длину касательной 
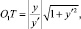подкасательной 
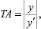нормали 
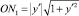и поднормали 
.
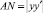Локальные координаты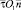 
в точке O1(x, y) связаны с декартовыми прямоугольными координатами xOy соотношениями
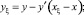
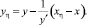
Орты единичной длины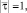 
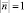, связанные с подвижной точкой O1(x, y) системы координат 
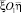, направлены по касательной 
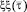и нормали 
.
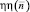Дополнительная декартова система x1O1y1 направлена аналогично системе xOy.
Радиус-вектор 
как инвариантный объект преобразуется из системы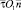 
криволинейных координат с компонентами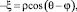 
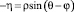в систему x1O1y1 с компонентами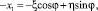 
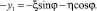
Производя подстановку значений ξ и η в два последних уравнения, запишем
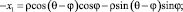
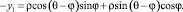
Разложение вектора 
с компонентами системы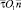 
на оси системы координат xOy будет иметь вид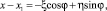 
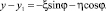
Для разделения переменных ξ и η в правых частях равенств выразим ξ из первого уравнения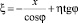 
и, подставив во второе, получим 
.
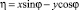Подставляя из этого равенства η в уравнение для x-компонента разложения, запишем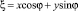 
.
В итоге получаем систему, в которой переменные ξ и η разделены:
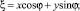
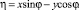
Дифференциальные характеристики кривой [2] y = f(x) позволяют, в частности, определить величины sin φ и cos φ (рис. 1).
Величины тригонометрических функций равны
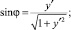
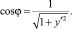
Производя подстановки в предыдущую систему, запишем
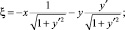
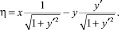
С учетом того, что уравнение кривой имеет вид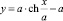 
, получим 
.
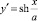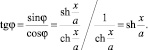
Подставляя в систему уравнений значение производной y′, перепишем систему в виде
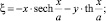
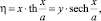
где учтены равенства
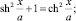
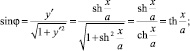
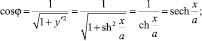
Полученные формулы преобразования координат ξ, η локальной ортогональной системы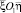 
могут быть использованы для представления решения, полученного в 
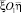, в декартовой системе координат xOy.
Преобразование произвольно расположенного на плоскости вектора 
, имеющего начало в точке O1(x, y), осуществляется аналогичным образом (рис. 2).
Компоненты вектора 
в дополнительной системе координат x1O1y1, преобразованные из системы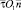 
, имеют вид
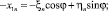
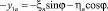
В системе xOy запишем с учетом равенств xn = –x1n и yn = –y1n:
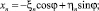
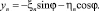
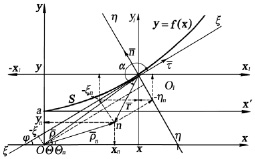
Рис. 2. Преобразование вектора 
из системы локальных координат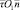 
в декартову xOy: 
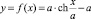– уравнение кривой
Следовательно, проекции вектора 
в системе координат xOy будут иметь вид
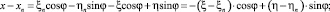
Отсюда, разделяя переменные (ξ – ξn) и (η – ηn), с учетом равенств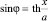 
и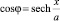 
для вектора 
с началом в точке O1(x, y) получим формулы преобразования:
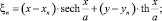
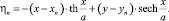
Качественная картина формирования течения в пределах струи, ограниченной отрезком Oa на оси ординат Oy лучом, совпадающим с абсциссой Ox и кривой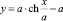 
, выглядит следующим образом.
Интенсивность слоя вихрей, вращающихся против часовой стрелки, длиной ds на кривой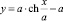 
имеет вид
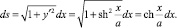
Интенсивность вихревого слоя длиной ds уменьшается в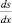 
раз и при интенсивности вихря 
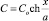остается постоянной и равной Co. При анализе индуцированных скоростей в системе координат 
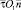принимается, что C = Co = const.
Каждый из вихрей возбуждает в струе две составляющие скорост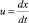и: 
и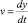 
. Движение сначала описывается в системе 
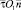подобно течению, возбуждаемому вихревым слоем длины S, а затем преобразуется в систему координат xOy. При этом длина слоя определяется формулой
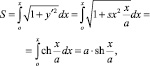
где x – проекция дуги S на ось Ox.
Пусть прямолинейные вихри нормальны плоскости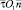 
и расположены вдоль отрицательного направления оси 
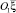на длине –S. Система координат инвертирована по отношению к квадранту (–ξ, O1, –η1), в котором расположен вихревой слой. На расстоянии ξn от начала координат O1 в положительном направлении оси 
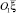располагается участок вихревого слоя того же направления вращения, что и вихревой слой в квадранте (–ξ, O1, –η1). Это обстоятельство вызвано тем, что отрезок кривой S соединяет начало системы координат 
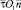– точку O1 и точку (0, a) координатной системы xOy, а вихревой слой продолжается за пределы точки O1 (рис. 3).
Таким образом, координаты оказываются отрицательными, как и длина кривой S.
В точке пространства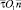 
элемент длиной –ds, расположенный на расстоянии –s от начала координат O1, возбуждает скорость 
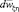, направленную по нормали к радиусу-вектору 
и равную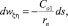 
где учтено, что величина ds отрицательна.
Вихревой слой имеет напряженность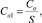 
отнесенную к длине кривой S.
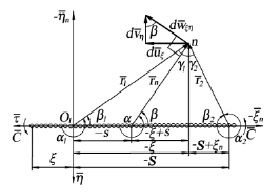
Рис. 3. Индуцирование скоростей непрерывным вихревым слоем конечной длины: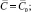 
β1 = π – α1; β2 = π – α2; n(–ξn, –ηn)
Компоненты вектора скорости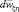 
, индуцированной вихревым отрезком ds, равны (рис. 3):
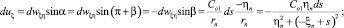
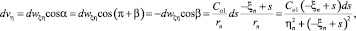
где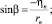 
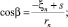
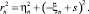
Полные компоненты скорости получатся интегрированием по длине слоя от 0 до S.
Компонент, направленный по оси –ξ, равен
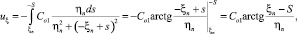
где интервал интегрирования начинается от ξn и заканчивается на границе S (рис. 3).
Компонент, направленный по оси –η, равен
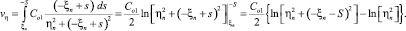
Подставляя уравнение вихревого слоя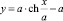 
в формулы преобразования координат точки конца радиуса-вектора, получим
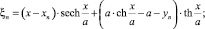
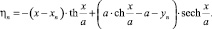
При известном годографе радиуса-вектора yn = f(xn) функции ξn = f(xn, yn), ηn = f(xn, yn) однозначно определяют величины скоростей uξ и vη, поскольку абсолютная величина вектора индуцированной скорости равна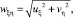 
а направление определяется величиной 
.
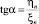Для определения величин скоростей на оси Ox системы координат xOy примем xn = x, а yn = 0, тогда для формул преобразования координат получим
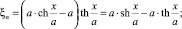
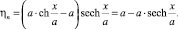
Подстановка этих формул в выражение для uξ позволяет записать
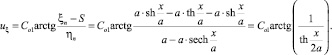
С учетом того, что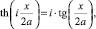 
запишем 
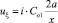или, отбрасывая мнимую единицу, окончательно,
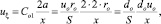
где do = 2ro – диаметр выходного сечения струебразующего насадка.
Полученное выражение с точностью до множителя совпадает с формулой для осевой скорости струи
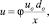
где φ – коэффициент в формуле А.Я. Миловича [3, 4].
Что касается нормальной составляющей vη, то она ответственна за вовлечение масс жидкости в струю из внешней области.
Таким образом, можно считать доказанным соответствие предлагаемой модели струи классической теории гидравлических струй.
Для упрощения функция скорости может быть определена по величине напряженности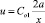 
, которая имеет размерность скорости, поскольку начальная напряженность вихря Co1 отнесена к длине границы струи S.
При точной постановке задачи величина индуцированной скорости должна определяться проектированием компонент скорости uξ и vη в точке на линии (x, –a), расположенной параллельно оси Ox и ниже ее на величину –a.
На этой линии находится слой грунта до размыва при горизонтальной оси струи.
Для наклонной рисбермы следует учитывать угол наклона концевой части, который, по Ц.Е. Мирцхулаве, равен θ [5].
Интерпретация результатов
Получена зависимость для величины продольной скорости потока, сходящего с концевого крепления флютбета от расстояния между крайней кромкой флютбета и нижерасположенным створом, соответствующая классическим зависимостям теории струй и уточняющая значение коэффициента скорости.
Рецензенты:
Мануковский А.Ю., д.т.н., профессор кафедры промышленного транспорта строительства и геодезии, ФГБОУ ВО «Воронежский государственный лесотехнический университет им. Г.Ф. Морозова», г. Воронеж;
Алибеков С.Я., д.т.н., профессор кафедры электроснабжения и технической диагностики, ФГБОУ ВПО «Марийский государственный университет», г. Йошкар-Ола.