При моделировании переноса бинарного электролита в электромембранных системах используется система уравнений Нернста – Планка [5], из которой, для определения концентрации, при выполнении условия электронейтральности можно получить уравнение конвективной диффузии. В работе [2] было показано, что использование уравнения конвективной диффузии при запредельных плотностях тока вызывает ряд сложностей. В данной работе предложен новый подход к 2D моделированию переноса симметричного бинарного электролита с одинаковыми коэффициентами диффузии катионов и анионов в ЭМС (электромембранных системах) при выполнении условия электронейтральности при запредельных плотностях тока. Суть нового подхода в использовании дифференциальных уравнений с частными производными первого порядка вместо уравнения конвективной диффузии. В данной работе этот подход обобщен для произвольного бинарного электролита с разными коэффициентами диффузии катионов и анионов и показано, что он позволяет оценить область пространственного заряда при запредельных плотностях тока.
1. Постановка задачи
1.1. Уравнения
Рассмотрим стационарный перенос бинарного электролита, тогда система уравнений Нернста – Планка и условия электронейтральности имеют следующий безразмерный вид [2]:
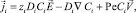 i = 1, 2; (1)
i = 1, 2; (1)
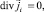 i = 1, 2; (2)
i = 1, 2; (2)
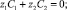 (3)
(3)
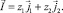 (4)
(4)
1.2. Геометрия
Рассмотрим половину канала обессоливания. Пусть x = 0 соответствует глубине раствора, где концентрация сохраняется постоянной, x = 1 соответствует условной границе раствор/катионообменная мембрана. При допредельных плотностях тока условие электронейтральности (9) выполняется везде за исключением погранслоя возле катионообменной мембраны, которая является областью пространственного заряда, половиной двойного электрического слоя (другая половина двойного электрического слоя расположена в мембране). При запредельных плотностях тока область пространственного заряда увеличивается при увеличении плотности тока и, соответственно, область электронейтральности уменьшается. В связи с этим возникает проблема оценки области электронейтральности при запредельных плотностях тока и определения закономерностей переноса ионов соли в этой области.
1.3. Граничные условия
Ниже приведены общепринятые граничные условия для системы уравнений (1)–(4).
1) В глубине раствора при x = 0:
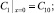
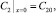
причем z1C10 + z2C20 = 0.
2) На поверхности КОМ при x = 1: 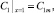 предполагается также, что КОМ идеально селективная, т.е. поток анионов j2 через катионообменную мембрану равен нулю
предполагается также, что КОМ идеально селективная, т.е. поток анионов j2 через катионообменную мембрану равен нулю 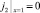 .
.
3) На входе в канал при y = 0:
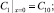
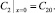
4) На выходе из канала при y = L:
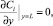 i = 1, 2.
i = 1, 2.
Замечание 1. Кроме граничных условий (1)–(4) на концентрацию, обычно задают следующие условия на потенциал φ: 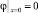 (т.е. прямая x = 0 является эквипотенциальной),
(т.е. прямая x = 0 является эквипотенциальной), 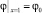 (т.е. поверхность КОМ (x = 1) является эквипотенциальной), на входе в канал задается распределение
(т.е. поверхность КОМ (x = 1) является эквипотенциальной), на входе в канал задается распределение 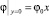 , на выходе «мягкое» условие
, на выходе «мягкое» условие 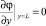 . При допредельных плотностях тока, величины φ0 и C1m связаны между собой [2]. Указанные выше условия на φ задают потенциостатический режим, однако для развиваемого нами в дальнейшем метода удобно будет переходить к гальваностатическому режиму. Между этими режимами существует однозначная связь. В гальваностатическом режиме задается средняя плотность тока iav по формуле
. При допредельных плотностях тока, величины φ0 и C1m связаны между собой [2]. Указанные выше условия на φ задают потенциостатический режим, однако для развиваемого нами в дальнейшем метода удобно будет переходить к гальваностатическому режиму. Между этими режимами существует однозначная связь. В гальваностатическом режиме задается средняя плотность тока iav по формуле
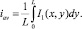
2. Декомпозиция
Покажем, что вместо исходной системы уравнений (1)–(4) для определения неизвестных C1, C2,  ,
, 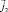 ,
, 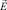 можно получить два уравнения для двух неизвестных функций, после решения которых остальные неизвестные могут быть найдены по формулам или по отдельным независимым уравнениям, то есть можно произвести расщепление (декомпозицию) исходной системы уравнений.
можно получить два уравнения для двух неизвестных функций, после решения которых остальные неизвестные могут быть найдены по формулам или по отдельным независимым уравнениям, то есть можно произвести расщепление (декомпозицию) исходной системы уравнений.
1. Обозначим C1 + C2 = S. Путем непосредственных вычислений проверяется справедливость формул (5), где
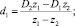
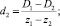
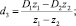
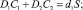
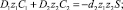 (5)
(5)
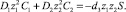
2. Сложим уравнения (1):
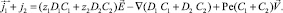
С учетом (5) имеем (6), где 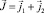 . Тогда уравнение (6) перепишем в виде (7).
. Тогда уравнение (6) перепишем в виде (7).
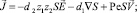 (6)
(6)
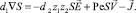 (7)
(7)
3. Сложим уравнения (1), умноженные соответственно на z1 и z2:
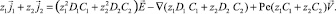
С учетом (3), (4) и (5) имеем 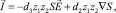 откуда следует
откуда следует
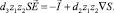 (8)
(8)
С учетом (8) из (7) для S получаем уравнение
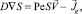 (9)
(9)
где 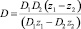 – коэффициент диффузии электролита и
– коэффициент диффузии электролита и 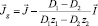 – общий суммарный поток.
– общий суммарный поток.
Таким образом, для решения системы уравнений (1–4) достаточно решить следующую систему уравнений (8), (9).
4. Из уравнений 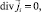 i = 1, 2 следует, что
i = 1, 2 следует, что  ,
,  ,
, 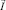 ,
, 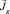 – соленоидальные вектора. Уравнения (8), (9) зависят от соленоидальных векторов
– соленоидальные вектора. Уравнения (8), (9) зависят от соленоидальных векторов 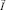 ,
,  и
и 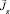 .
.
Уравнения, не зависящие от соленоидальных векторов 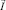 ,
,  и
и 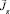 , можно получить, если взять div от обеих частей (8), (9), тогда получим уравнение конвективной диффузии для функции S (10) и уравнение переноса для
, можно получить, если взять div от обеих частей (8), (9), тогда получим уравнение конвективной диффузии для функции S (10) и уравнение переноса для 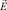 :
: 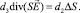 Это уравнение обычно записывают для потенциала с учетом
Это уравнение обычно записывают для потенциала с учетом 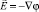 , тогда получаем (11).
, тогда получаем (11).
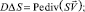 (10)
(10)
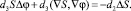 (11)
(11)
Для решения уравнений (10), (11) необходимо ставить дополнительные граничные условия из-за того, что получились дифференциальные уравнения более высокого порядка. Общепринятая практика, наряду с переходом к уравнениям (10), (11), заключается в том, что ставятся граничные условия при x = 1, например условие
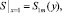 (12)
(12)
причем S1m(y) > 0, поскольку S является суммарной концентрацией. Из этого сразу следует, что такая задача моделирует лишь допредельный режим iav < ilim = 2 [2]. Если же положить 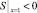 , то задача для пары функций
, то задача для пары функций 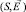 не имеет решение [2].
не имеет решение [2].
Дифференциальные уравнения (10), (11) при запредельных плотностях тока можно рассматривать как краевые задачи в области с неизвестной правой границей и необходимо при этом доопределить краевые условия. Пусть нули функции S описываются формулой x = q(y), y ∈ [0, L], т.е. S(q(y), y) = 0 для любого y ∈ [0, L]. Обозначим S решение краевой задачи: 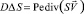 в области
в области 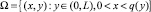 :
: 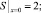 S(q(y), y) = 0;
S(q(y), y) = 0; 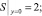 ΔS(q(y), y) = 0;
ΔS(q(y), y) = 0; 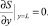 Таким образом, для S получаем переопределенную краевую задачу с неизвестной границей. Решение таких задач является достаточно сложной проблемой [1].
Таким образом, для S получаем переопределенную краевую задачу с неизвестной границей. Решение таких задач является достаточно сложной проблемой [1].
Таким образом, можно сделать вывод, что общепринятый подход, связанный с увеличением порядка уравнений, усложняет задачу и его удобно использовать лишь при допредельных плотностях тока.
3. Вспомогательное уравнение 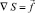
Рассмотрим решение уравнения 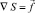 в 2D односвязной области Ω при известном гладком векторе
в 2D односвязной области Ω при известном гладком векторе 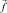 .
.
Определим двумерный аналог оператора rot, – оператор
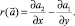
Необходимым и достаточным условием разрешимости уравнения 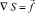 является условие
является условие 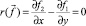 или
или 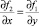 , при этом решение выражается формулой [2]:
, при этом решение выражается формулой [2]:
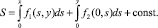
Аналогично можно получить формулу
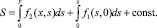
Формулу для S можно записать симметрично:
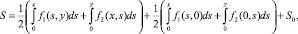
где S0 = S(0, 0) – некоторая постоянная.
Таким образом, для однозначного решения системы уравнений 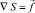 достаточно условия S(0, 0) = S0.
достаточно условия S(0, 0) = S0.
4. Непосредственное решение системы уравнений (9)
Так как 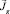 некоторый соленоидальный вектор, то существует функция γ, что
некоторый соленоидальный вектор, то существует функция γ, что
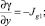
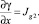
4.1. Условие разрешимости
Обозначим 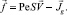 Согласно п. 3 условие разрешимости уравнения (9) –
Согласно п. 3 условие разрешимости уравнения (9) – 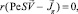 откуда получаем уравнение для функции γ:
откуда получаем уравнение для функции γ:
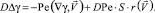
К этому уравнению добавляем уравнение (9) и получаем систему из двух уравнений с двумя неизвестными γ и S:
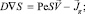 (13)
(13)
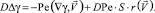 (14)
(14)
4.2. Граничные условия
Из граничных условий для C1 и C2 для функции S получаются граничные условия
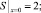
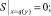
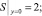
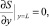 (15)
(15)
Наряду с граничными условиями (15) на функцию S необходимы граничные условия для функции γ. Как следует из п. 3, условия (15) избыточны для нахождения решения уравнения (13) и должны выводится граничные условия для функции γ.
С учетом (13) и (15) для вектора 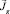 получаем
получаем
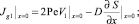
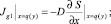
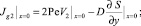
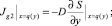
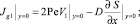
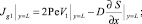
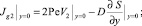
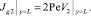
В силу условий (15) имеем 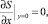
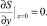 Откуда с учетом
Откуда с учетом 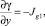
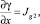 получаем граничные условия для функции γ:
получаем граничные условия для функции γ:
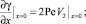
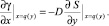 (16)
(16)
Как видно, из уравнения (14) и граничных условий (16) функция γ определяется с точностью до постоянной величины.
Определим конкретное значение функции γ и свяжем его с заданной плотностью тока. Для этого воспользуемся соотношением  .
.
В силу идеальной селективности катионообменной мембраны j1,1 >> j2,1 (в одномерном случае вообще j2 = 0 и j1 = iav), поэтому J1,1 ≈ I1,1. Следовательно,
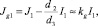
где 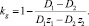
Таким образом, средний ток iav может быть определен следующей формулой
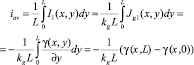
или
γ(x, L) – γ(x, 0) = –kgLiav.
Поскольку функция γ определяется с точностью до постоянной величины, то можно положить, например, γ(x, L) = 0, тогда γ(x, 0) = –kgLiav. Заметим что если D1 = D2, то kg = 1.
Итак, для нахождения функций γ и S имеем краевую задачу
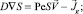 (17)
(17)
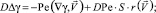 (18)
(18)
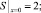
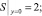
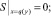 (19)
(19)
γ(x, L) = 0; γ(x, 0) = –kgLiav; (20)
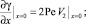
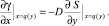 (21)
(21)
5. Решение краевой задачи (17)–(21)
5.1. Метод последовательных приближений
Для решения краевой задачи (17)–(21) можно использовать следующий метод последовательных приближений:
1) Возьмем некоторый соленоидальный вектор 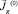 .
.
2) Найдем решение S(0), уравнения 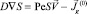 , удовлетворяющее граничным условиям при x = 0 и y = 0.
, удовлетворяющее граничным условиям при x = 0 и y = 0.
3) Найдем нули функции S(0), т.е. такую функцию x = q(0)(y), y ∈ [0, L], что S(0)(q(0)(y), y) = 0, y ∈ [0, L].
4) Найдем решение γ(1) уравнения
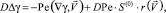
в области
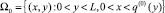 ,
,
удовлетворяющее соответствующим граничным условиям (20), (21).
5) Найдем 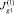 и
и 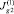 по формулам
по формулам
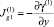 и
и 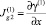 .
.
6) Найдем решение S(1) уравнения 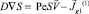 , удовлетворяющее соответствующим граничным условиям.
, удовлетворяющее соответствующим граничным условиям.
7) Проверим условие сходимости 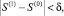 где δ – заданная точность. Если условие сходимости выполняется, S(1) принимаем за решения, иначе полагаем
где δ – заданная точность. Если условие сходимости выполняется, S(1) принимаем за решения, иначе полагаем 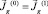 и идем к п. 2.
и идем к п. 2.
5.2. Решение краевой задачи асимптотическим методом при небольших числах Пекле
Если Pe << 1, т.е. скорость прокачки раствора небольшая, то функции γ и S можно разложить по степеням Pe:
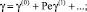
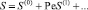
Подставляя эти разложения в систему уравнений (17), (18) и краевые условия (19), (20) и приравнивая коэффициенты при одинаковых степенях в каждом уравнении и граничном условии, получаем краевые задачи для коэффициентов разложения. Для простоты изложения приведем краевые задачи лишь для первых двух приближений.
Для γ(0), S(0) получаем краевую задачу:
DΔγ(0) = 0; (22)
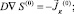 (23)
(23)
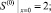
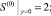
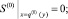 (24)
(24)
γ(0)(x, L) = 0; γ(0) (x, 0) = –kgLiav; (25)
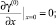
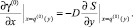 (26)
(26)
Для γ(1), S(1) получаем краевую задачу:
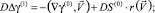 (27)
(27)
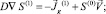 (28)
(28)
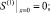
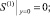
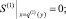 (29)
(29)
γ(1)(x, L) = 0; γ(1)(x, L) = 0; (30)
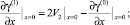
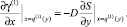 (31)
(31)
1) Решение краевой задачи для начального приближения γ(0), S(0)
Рассмотрим два разных метода решения краевой задачи.
Первый метод. Сначала решаем краевую задачу для уравнения 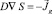 аналитически и находим
аналитически и находим 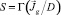 , где Γ интегральный оператор (см. п. 3). Далее находим решение уравнения DΔγ = 0 в области Ω, с заранее неизвестной границей, определяемой дополнительным условием
, где Γ интегральный оператор (см. п. 3). Далее находим решение уравнения DΔγ = 0 в области Ω, с заранее неизвестной границей, определяемой дополнительным условием 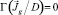 и граничным условием
и граничным условием 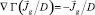 на этой границе.
на этой границе.
Второй метод. Если для решения использовать метод последовательных приближений п. 5.1, то получаем, что сначала задается некоторый соленоидальный вектор 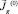 . Затем находим
. Затем находим 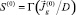 и определяем градиент
и определяем градиент 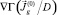 и нули x = q(0)(y) функции S(0). Далее решаем уравнение DΔγ = 0 в области
и нули x = q(0)(y) функции S(0). Далее решаем уравнение DΔγ = 0 в области 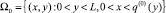 , удовлетворяющее соответствующим граничным условиям, и далее по алгоритму п. 5.1.
, удовлетворяющее соответствующим граничным условиям, и далее по алгоритму п. 5.1.
2) Решение краевой задачи для первого приближения γ(1), S(1)
Краевая задача для γ(1), S(1) отличается от краевой задачи для γ(0), S(0) лишь тем, что уравнение для γ(1) неоднородное, а для S(1) граничные условия однородные. Поэтому краевая задача для γ(1), S(1) решается аналогично краевой задаче для γ(0), S(0).
6. Случай течения Пуазейля
6.1. Упрощение краевой задачи для течения Пуазейля
В гладком канале независимо от начального распределения скорости течение раствора достаточно быстро становится Пуазейлевским. Для половины канала это означает
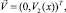
где 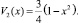
В этом случае из (17)–(21) имеем
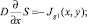 (32)
(32)
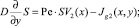 (33)
(33)
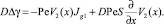 (34)
(34)
6.2. Сведение краевой задачи (32)–(34) к краевой задаче для интегро-дифференциального уравнения
Из уравнения (32) с учетом граничного условия S(0, y) = 2 для любого y ∈ [0, L] получаем
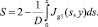 (35)
(35)
С другой стороны, применяя общую формулу п. 3, с учетом 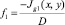 и
и 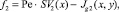 получаем
получаем
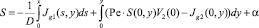
или
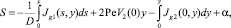
где α постоянная, не зависящая от x, y. Эта формула согласуется с формулой (35) в силу граничных условий
α = 2 и 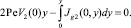
Действительно, второе соотношение, как легко видеть после дифференцирования по y, эквивалентно граничному условию
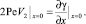
Подставляя (35) в уравнение (34), получаем для функции γ краевую задачу для интегро-дифференциального уравнения:
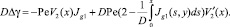 (36)
(36)
с соответствующими граничными условиями (20), (21).
6.3. Решение краевой задачи для интегро-дифференциального уравнения методом последовательных приближений
Краевую задачу для интегро-дифференциального уравнения (36) можно решать, например, методом последовательных приближений
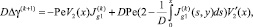 k = 0, 1, ... (37)
k = 0, 1, ... (37)
в области 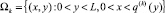 , с граничными условиями (19)–(21).
, с граничными условиями (19)–(21).
Пусть 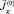 некоторый соленоидальный вектор, S(0) рассчитывается по формуле
некоторый соленоидальный вектор, S(0) рассчитывается по формуле 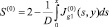 . Находим x = q(0)(y) – нули функции S(0). Решая краевую задачу для выражения (37) при k = 0, находим функции γ(1),
. Находим x = q(0)(y) – нули функции S(0). Решая краевую задачу для выражения (37) при k = 0, находим функции γ(1), 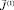 , а затем функцию S(1) и т.д.
, а затем функцию S(1) и т.д.
6.4. Пример вычисления последовательных приближений
Рассмотрим для простоты симметричный 1:1 электролит с D1 = D2 при запредельных токовых режимах iav > ilim = 2. Тогда уравнение и краевые условия упростятся, так как тогда D = 1 и kg = 1, причем
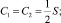
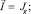
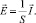
1) Положим 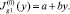 Выберем a и b так, чтобы на входе в канал был предельный режим и удовлетворялись граничные условия (20), т.е.
Выберем a и b так, чтобы на входе в канал был предельный режим и удовлетворялись граничные условия (20), т.е.  и
и 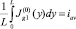 или
или 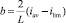 . Таким образом
. Таким образом 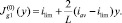
2) Вычислим S(0) по формуле (35).
3) Найдем область
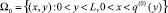 .
.
Для этого найдем нули функции
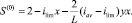
Таким образом
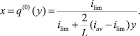
Область
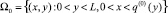
является начальным приближением области электронейтральности при заданной запредельной плотности тока iav (iav > ilim = 2).
4) Решим уравнение (37) при k = 0
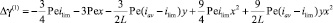
в области 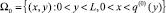 , с краевыми условиями
, с краевыми условиями
γ(1)(x, L) = 0; γ(1)(x, 0) = Liav; 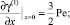
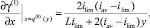
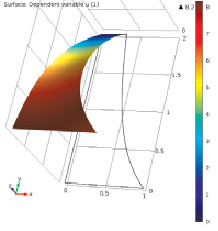
Рис. 1. График функции γ(1)
5) Находим 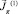 , а затем функцию S(1).
, а затем функцию S(1).
6) Находим нули функции S(1), т.е. функцию x = q(1)(y) и определяем очередное приближение к области электронейтральности 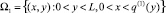 и т.д.
и т.д.
7) Результаты численных экспериментов.
Ниже приведены результаты численного решения при iav = 2ilim = 4, Pe = 0,1.
Функция γ(1) является нелинейной, положительно определенной функцией, причем нелинейность функции по x связана с нелинейность по x свободного члена уравнения, а нелинейность по y с граничным условием на правой границе.
Сопоставление графиков 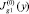 и
и 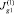 показывает, что следующая итерация приводит к коррекции начального линейного приближения
показывает, что следующая итерация приводит к коррекции начального линейного приближения 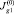 зависящего только от одной переменной y и замене его на нелинейную функцию
зависящего только от одной переменной y и замене его на нелинейную функцию 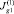 от обоих аргументов. Кроме того, видно, что в конце канала
от обоих аргументов. Кроме того, видно, что в конце канала 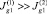 , т.е. ток течет практически поперек канала. Это связано с тем, что число Pe = 0,1 небольшое.
, т.е. ток течет практически поперек канала. Это связано с тем, что число Pe = 0,1 небольшое.
a б в
Рис. 2. Графики функций: a – 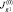 ; б –
; б – 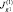 ; в –
; в – 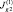
a б
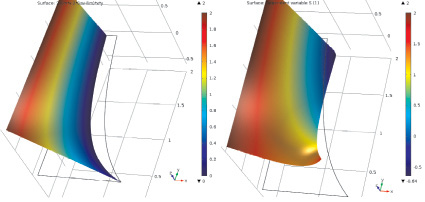
Рис. 3. Графики: a – S(0); б – S(1)
а б
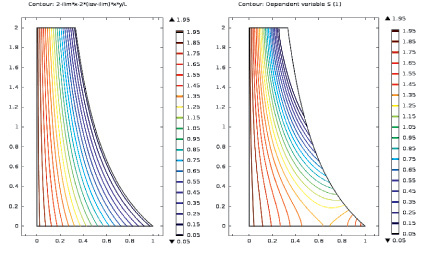
Рис. 4. Линии уровня: a – S(0); б – S(1)
Поскольку в данном случае 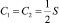 , то концентрация катионов и анионов может быть проанализирована по виду функции S. На а и б видно наличие «плато» в ядре потока и снижение концентрации до нуля на правой границе. Наличие отрицательных значений у функции S(1) в отличие от начального приближения S(0) говорит о том, что следующее приближение Ω1 к области электронейтральности отличается от начального приближения Ω0. Более ясно это видно на рис. 4, б, – в верхнем правом углу области часть области электронейтральности в приближении Ω0 в следующем приближении Ω1 уже исключается (не заштрихованная область в криволинейной трапеции Ω0) и правая граница области электронейтральности уточняется.
, то концентрация катионов и анионов может быть проанализирована по виду функции S. На а и б видно наличие «плато» в ядре потока и снижение концентрации до нуля на правой границе. Наличие отрицательных значений у функции S(1) в отличие от начального приближения S(0) говорит о том, что следующее приближение Ω1 к области электронейтральности отличается от начального приближения Ω0. Более ясно это видно на рис. 4, б, – в верхнем правом углу области часть области электронейтральности в приближении Ω0 в следующем приближении Ω1 уже исключается (не заштрихованная область в криволинейной трапеции Ω0) и правая граница области электронейтральности уточняется.
Полученные выше результаты согласуются с физическими представлениями и решениями одномерных моделей переноса бинарного электролита [4].
Замечание 2. Если V2(x) = const = V0, уравнение (33) не зависит от S и имеет вид 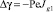 или
или 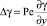 . Решая это уравнение с соответствующими условиями, находим
. Решая это уравнение с соответствующими условиями, находим 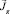 и по формуле (34) находим функцию S.
и по формуле (34) находим функцию S.
Замечание 3. Метод 2D моделирования, развитый здесь для бинарного электролита, несложно обобщается на случай произвольного числа ионов.
Заключение
Общепринятый метод моделирования переноса бинарного электролита в ЭМС при выполнении условия электронейтральности, заключается в использовании уравнения конвективной диффузии, т.е. уравнения с частными производными второго порядка. В работе предложен новый подход к 2D моделированию переноса бинарного электролита в ЭМС при тех же условиях, использующий уравнение с частными производными первого порядка, для решения которого не требуется граничного условия на концентрацию на поверхности мембраны. Это позволяет моделировать перенос ионов соли как при допредельных, так и запредельных плотностях тока, определять границы области электронейтральности.
Полученные в работе результаты могут быть использованы в нанотехнологиях, мембранной электрохимии и микрофлюидике при моделировании и исследовании переноса бинарного при запредельных плотностях тока [3, 6–7].
Работа выполнена при финансовой поддержке РФФИ и администрации Краснодарского края грантов: № 13-08-93105-НЦНИЛ_а и 13-08-96519 р_юг_а.
Рецензенты:
Халафян А.А., д.т.н., доцент, профессор кафедры прикладной математики, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар;
Павлова А.В., д.ф.-м.н., доцент, профессор кафедры математического моделирования, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар.



