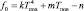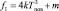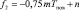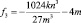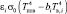Заполярные территории относятся к районам со сложными природно-климатическими и инженерно-геологическими условиями. Корректный расчет температурного режима грунтов криолитозоны необходим для обеспечения требуемого уровня надежности сооружений. Наибольшую опасность представляют термически неустойчивые просадочные многолетнемерзлые грунты (ММГ) с высокой влажностью [1–8; 11–13; 15].
В нормативно-технической документации РФ утверждена методика расчета температурного режима ММГ, которая учитывает влияние температурного режима воздуха, солнечной радиации, скорости ветра и снежного покрова, но не учитывает теплообмен подстилающей поверхности грунта с атмосферой в инфракрасной области спектра [14]. Проведенные ранее исследования показывают, что инфракрасное излучение оказывает существенное влияние на результаты прогнозных теплотехнических расчетов [9, 10].
Цель работы – разработать методику задания граничных условий третьего рода, учитывающую теплообмен с атмосферой посредством инфракрасного излучения и термическое сопротивление снежного покрова и обосновать необходимость ее применения.
Задачи:
– проанализировать исходные данные, необходимые для выполнения расчета температурного режима ММГ;
– вывести формулу для задания граничных условий третьего рода на поверхности грунта;
– обосновать необходимость введения поправки на теплообмен посредством инфракрасного излучения.
Моделирование температурного режима ММГ (рисунок) выполняется путем численного решения дифференциального уравнения теплопроводности методом конечных элементов или конечных разностей:
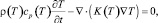 (1)
(1)
где ρ(T) – плотность грунта; T – температура; cр(T) – теплоемкость грунта; t – время; K(T) – теплопроводность грунта.
На нижней и боковых поверхностях моделируемого массива грунта выбирается граничное условие типа «нулевой тепловой поток». На поверхности грунта задается граничное условие:
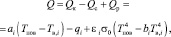 (2)
(2)
где Q – тепловой поток от грунта в атмосферу; Qк – конвективный тепловой поток; Qс – поток тепла от солнечной радиации; Qр – радиационный поток тепла в ИК области спектра; a – коэффициент конвективной теплоотдачи подстилающей поверхности грунта; qi – поток тепла от солнечной радиации; εi – степень черноты подстилающей поверхности грунта; σ0 – постоянная Стефана – Больцмана; bi – коэффициент излучения атмосферы; индекс i относится к i-му месяцу в году.
Выражение (2) полностью описывает тепловой поток в периоды времени, когда снежный покров отсутствует. Однако учет снежного покрова методом эквивалентного термического сопротивления усложняет задачу. Появляется дополнительная неизвестная величина – температура поверхности снега. Далее мы займемся выводом формулы, задающей тепловой поток от поверхности грунта в атмосферу через снежный покров.
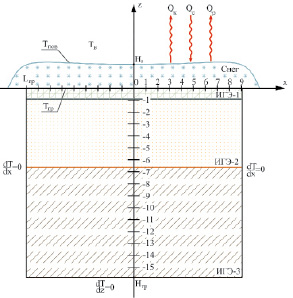
Схема для моделирования температурного режима многолетнемерзлых грунтов и основные граничные условия: Hs – высота снежного покрова; Hгр – глубина моделируемого грунтового основания, соответствующая границе нулевой годовой амплитуды температуры; Lгр – ширина моделируемого грунтового основания; Tпов – температура подстилающей поверхности грунта; Tв – температура атмосферного воздуха; Tгр – температура грунта; ИГЭ-1, 2, 3 – инженерно-геологические элементы
При задании динамики теплоизоляционных свойств снежного покрова методом эквивалентного термического сопротивления существенным является тот факт, что тепловой поток через толщу снега считается квазистационарным, т.е. постоянным в любой момент времени. Как следствие, принимается линейное распределение температур. Такой подход имеет хорошее приближение к действительности, если заранее известна динамика толщины, плотности и теплопроводности снежного покрова.
Величина теплового потока через снежный покров в случае стационарного теплового потока имеет следующий вид (3):
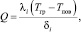 (3)
(3)
где λi – коэффициент теплопроводности снега; δi – толщина снежного покрова.
Теперь мы имеем систему из двух уравнений (2) и (3) и две неизвестные величины: Q и Tпов. Приравняем уравнения (2) и (3) друг к другу, исключив из рассмотрения величину теплового потока Q:
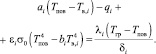 (4)
(4)
Как видно, уравнение (4) является полиномиальным, четвертой степени относительно неизвестной переменной Tпов. Сгруппируем коэффициенты при одинаковых степенях в формуле (4):
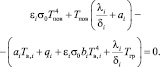 (5)
(5)
Заметим, что все числовые множители мономов в уравнении (5) являются положительными. В соответствии с физическим смыслом задачи нам необходимо найти температуру подстилающей поверхности грунта (температуру поверхности снега в зимний период времени), которая может принимать значения в диапазоне от 0 до ∞.
В связи с громоздкостью окончательного выражения для Tпов мы не будем получать решение в явном виде. Мы лишь докажем, что решение уравнения (5) существует и единственно для данной задачи. Для доказательства применим теорему Штурма. Найдем все полиномы штурма и запишем число смены знаков в полиномах штурма для исследуемых интервалов (табл. 1).
Зная число смены знаков в полиномах Штурма, определим количество действительных положительных корней уравнения N:
N = w(inf) – w(0) = 2 – 1 = 1. (6)
Таким образом, доказано существование единственного положительного корня уравнения (5), а значит и однозначная разрешимость системы уравнений (2)–(3). Благодаря тому, что степень уравнения (5) не превышает четырех, становится возможным найти аналитическое решение, например, по формулам Декарта – Эйлера. Решение для Tпов подставляется в уравнение (3) или (4) и находится величина теплового потока Q.
Теперь рассмотрим влияние снежного покрова на соотношение тепловых потоков различного рода. Исходные данные и результаты расчетов приведены в табл. 2.
Таблица 1
Определение числа смены знаков в полиномах Штурма
|
Граница диапазона Полиномы штурма |
0 |
inf |
|
|
– |
+ |
|
|
+ |
+ |
|
|
+ |
– |
|
|
– |
– |
|
Число смены знаков, w |
2 |
1 |
Таблица 2
Оценочный расчет слагаемых конвективного и радиационного теплообмена
|
Основные виды теплообмена Последовательность расчета |
Конвективный тепловой поток ai (Tпов – Tв, i) |
Поток тепла от солнечной радиации qi |
Тепловой поток ИК излучения
|
|
Исходные данные |
ai = 30 Вт/(К∙м2) (Tгр – Tв, i) = 5 К |
qi = 0 Вт/м2 (полярная ночь) |
εi = 0,9 (для снега) σ0 = 5,67∙10–8 Вт/(м2∙К4) Tв, i = 248 К Tгр = 253 К bi = 0,89 |
|
Термическое сопротивление снежного покрова, δi/λi, м2/Вт |
0,1…5 |
||
|
Температура поверхности снега, К |
248,66…247,39 |
||
|
Величина теплового потока от грунта в атмосферу, Вт/м2 |
20,01…–18,23 |
0 |
23,32…19,34 |
|
Вклад в суммарный тепловой поток, % |
46,2…48,51) |
0 |
53,8...51,51) |
Примечание. 1 – вклад в суммарный тепловой поток вычислен от суммы модулей величин конвективного и радиационного теплового потока.
Из табл. 2 видно, что абсолютная величина теплового потока от инфракрасного излучения почти всегда преобладает над конвективным тепловым потоком. Более того, при увеличении толщины снежного покрова конвективный тепловой поток меняет свой знак на противоположный. Это обусловлено тем, что радиационная температура атмосферы ниже температуры воздуха. Как следствие, наблюдается переохлаждение приповерхностных слоев снега до температур, более низких, чем температура атмосферного воздуха. Такой эффект может быть обнаружен только в том случае, если в расчете учитывается радиационный тепловой поток в инфракрасной области спектра по закону Стефана – Больцмана. Его учет является обязательным условием достоверного описания процесса теплопередачи от грунта в атмосферу. Это является очередным подтверждением выводов работ [9, 10].
Выводы
Выявлено, что методика расчета температурного режима ММГ, закрепленная в нормативно-технической документации РФ, не учитывает радиационный теплообмен в инфракрасной области спектра. Анализ научно-технической литературы показал, что неучёт данного вида теплообмена приводит к существенному искажению результатов моделирования теплового взаимодействия подземных сооружений с ММГ [9, 10]. Выведена система уравнений для задания граничных условий третьего рода на поверхности грунта, учитывающая теплообмен в инфракрасной области спектра и задающая снежный покров методом эквивалентного термического сопротивления. Доказана единственность решения системы уравнений для данной задачи. Показано, что теплообмен в инфракрасной области спектра вносит существенный вклад в температурный режим ММГ и его учет необходим для обеспечения высокой степени достоверности результатов моделирования.
Рецензенты:
Якубовский Ю.Е., д.т.н., заведующий кафедрой «Прикладная механика», ФГБОУ ВО «Тюменский государственный нефтегазовый университет», г. Тюмень;
Тарасенко А.А., д.т.н., профессор кафедры ТУР, ФГБОУ ВО «Тюменский государственный нефтегазовый университет», г. Тюмень.