При решении задач создания алгоритмов противопожарного мониторинга и локального пожаротушения при помощи малых беспилотных летательных аппаратов – квадрокоптеров, появляется научная проблема эффективной стабилизации движения, точного выполнения маневров и удержания положения квадрокоптером в пространстве. В последнее время был достигнут значительный прогресс в системах управления полетной динамикой квадрокоптера, последние образцы включают в себя агрессивные маневры [7], игру в теннис [11] и задачи совместной постройки простых конструкций [9]. В то же время все данные системы требуют наличия внешней системы мониторинга движения и не могут быть использованы в задачах противопожарного мониторинга, а также пожаротушения и применения в экстремальных ситуациях.
Эффективное автономное управление полетом до сих является открытой научной проблемой, особенно там, где невозможно применить внешние системы позиционирования – такие как GPS или GLONASS. Главной задачей, составляющей данную проблему, является сложность качественного позиционирования с использованием лишь встроенных сенсоров.
Задача точного измерения движения в произвольном и неизвестном заранее пространстве является одной из главных в области компьютерного зрения и робототехники и широко известна как проблема одновременной навигации и составления карты (simultaneous localization and mapping – SLAM). Идея очень проста – составлять карту окружающего пространства, используя сенсоры. Карта в дальнейшем используется для повторного определения текущей позиции через некоторый период времени. Таким образом SLAM отвечает на вопросы «Как выглядит окружающий мир?» и «Где я нахожусь?».
Для решения проблемы SLAM в данное время предлагается использовать самые различные сенсоры, такие как стереокамеры [3], лазерные сканеры – лидары [8], RGB-D камеры [4]. Данные решения неоправданно использовать для решения проблемы SLAM на малых БПЛА в качестве средства противопожарного мониторинга и локального пожаротушения в связи с их дороговизной и тяжелым весом – предполагаемая потеря БПЛА не должна принести значительного финансового ущерба.
Рассмотрим данную проблему на примере малого БПЛА с четырьмя фиксированными роторами – квадрокоптера. С нашей точки зрения, встроенные в квадрокоптер легкие и недорогие камеры имеют значительное преимущество в том, что их радиус действия не ограничен, позволяя применять однообъективный SLAM как внутри помещений, так и на открытых производственных площадках. Однако существует ряд ограничений, так как масштаб окружающего мира не может быть определен при помощи одного лишь изображения – необходимы дополнительные источники данных, и в случае с квадрокоптером наиболее целесообразно использовать данные инерциальных измерений IMU (Inertial measurements unit – устройство для осуществления инерциальных измерений).
Комбинация инерциальных и визуальных измерений может быть разделена на три типа использования. Первый – применение результатов измерений одного типа сенсора в качестве корректирующего к результатам измерений другого типа. Второй – использование лишь некоторых инерциальных измерений совместно с результатами визуальных наблюдений. Третий – объединение результатов инерциальных и визуальных измерений для улучшения определения положения.
В данной работе используется третий тип использования. Целью данной работы является создание алгоритмов стабилизации и управления полетом малого автономного БПЛА – квадрокоптера, пригодных для применения в чрезвычайной ситуации.
Существующие публикации по управлению квадрокоптером могут быть разделены на различные области исследований. Часть исследований посвящена точному управлению квадрокоптером [10], но данные работы в значительной мере опираются на внешние системы управления движением, ограничивая их применение исключительно в лабораторных условиях. Другие подходы используют заранее записанную в ручном режиме управления траекторию и дальнейшее ее повторение в автоматическом режиме [6].
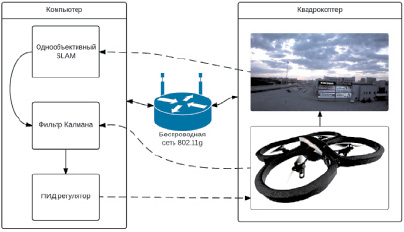
Рис. 1. Графическое представление предложенного подхода, состоящего из трех элементов: однообъективный SLAM для визуального трекинга, фильтр Калмана для обработки данных и ПИД регулятор для генерации управляющих команд. Все вычисления производятся на внешнем устройстве, что приводит к значительным задержкам поступления измерений и управляющих команд
В нашем подходе мы фокусируемся на стабилизации квадрокоптера с использованием визуальных данных с возможностью автономного полета по заданным траекториям без исходных знаний об окружающей среде и в отсутствие GPS-сигнала с применением лишь имеющихся на борту сенсоров. Стабилизация с использованием визуальных данных была впервые представлена в [12], однако данный метод имеет свойство накапливать ошибки с течением времени и не подходит для длительных автономных полетов.
Для компенсации накопления ошибки было предложено использование множества различных методов SLAM [1, 2], однако серьезной проблемой является определение масштаба, и оно не может быть совершено без привлечения дополнительных сенсоров, таких как IMU.
В качестве лабораторной платформы используется квадрокоптер Parrot AR.Drone 2.0, доступный в свободной продаже. В сравнении с квадрокоптерами фирм DJI или Ascending Technologies преимуществами являются невысокая цена, высокая надежность и доступность запасных частей. Стандартная комплектация также включает в себя защитную рамку, которая позволяет безопасно выполнять полеты внутри помещений. В то же время ни программное, ни аппаратное обеспечение данной модели невозможно заменить или изменить стандартными методами; связь с квадрокоптером доступна только через беспроводную сеть стандарта 802.11g. Вес со стандартной батареей и рамкой для полетов внутри помещений составляет около 420 грамм.
Квадрокоптер укомплектован 3-осевыми гироскопом и акселерометром, ультразвуковым альтиметром и двумя камерами. Первая камера направлена вперед, имеет разрешение 640×480, угол обзора составляет 93° и обладает дефектом rolling shutter с задержкой около 40мс между первой и последней захваченной линией. Видео с фронтальной камеры транслируется на компьютер с частотой 20 кадров в секунду. Вторая камера направлена вниз, имеет разрешение 320×240 и угол обзора 64°; используется встроенным программным обеспечением для определения горизонтальной скорости. Квадрокоптер транслирует данные гироскопа и горизонтальную скорость с частотой 200 Гц, ультразвуковой альтиметр передает данные с частотой 25 Гц. Исходные, не модифицированные встроенным программным обеспечением данные недоступны для использования. Встроенное программное обеспечение использует эти сенсоры для управления по каналам крена Φ и тангаж Ψ, в то время как скорость рыскания 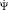 и вертикальная скорость
и вертикальная скорость  задаются при помощи внешнего эталонного значения u. Это значение устанавливается каждые 10 мс отправкой управляющей команды
задаются при помощи внешнего эталонного значения u. Это значение устанавливается каждые 10 мс отправкой управляющей команды 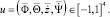
Наш подход состоит из трех основных компонентов, которые выполняются на ноутбуке, подключенном к квадрокоптеру через беспроводную сеть.
1. Однообъективный SLAM. Для реализации однообъективного SLAM наш подход использует библиотеку PTAM – Parallel Tracking and Mapping [5]. После инициализации карты производится вращение карты в плоскости x, y в соответствии с данными акселерометра, и масштабирование с параметром средней глубины ключевой точки равным 1. В дальнейшем масштабирование полученной карты выполняется при помощи метода, описанного ниже. Также определяется положение квадрокоптера в пространстве применением расширенного фильтра Калмана для определения и отбрасывания некорректных измерений.
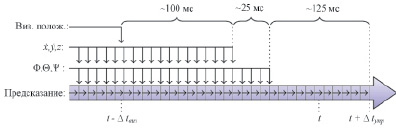
Рис. 2. Предсказание положения. Измерения и управляющие команды поступают со значительными задержками. Для их компенсации предлагается хранить историю измерений и посылать управляющие команды между t – Δtвиз и t – Δtупр
2. Расширенный фильтр Калмана. Для комбинирования и фильтрации всех получаемых данных применяется расширенный фильтр Калмана (EKF). Нами была рассчитана и откалибрована комплексная модель динамики полета квадрокоптера и его реакции на управляющие команды, детали которой описаны далее. Также EKF используется для компенсации различных временных задержек в системе, появляющихся в результате UDP/IP коммуникации в беспроводной сети, а также во время вычисления визуального трекинга (рис. 2).
3. PID управление. ПИД регулятор применяется для вычисления управляющих команд и направления квадрокоптера к желаемой позиции 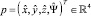 в глобальной системе координат. В соответствии с текущим состоянием мы преобразуем полученные управляющие команды в систему относительно самого робота и передаем команды квадрокоптеру. Для каждой из 4 степеней свободы используется отдельный ПИД контроллер, тип которого был экспериментально определен как наиболее подходящий.
в глобальной системе координат. В соответствии с текущим состоянием мы преобразуем полученные управляющие команды в систему относительно самого робота и передаем команды квадрокоптеру. Для каждой из 4 степеней свободы используется отдельный ПИД контроллер, тип которого был экспериментально определен как наиболее подходящий.
Графическое представление предложенного подхода изображено на рис. 1.
Применение EKF к наблюдению и предсказанию. Область состояния состоит из 10 переменных:
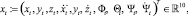 (1)
(1)
где (xt, yt, zt) обозначает текущую позицию квадрокоптера в метрах и 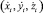 скорость в метрах в секунду в мировых координатах, крен Φt, тангаж Θt, рыскание Ψt и угловую скорость
скорость в метрах в секунду в мировых координатах, крен Φt, тангаж Θt, рыскание Ψt и угловую скорость 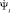 в градусах/с. В дополнение для каждого сенсора определяется функция наблюдения h(xt), которая описывает, как вектор наблюдений zt вычисляется из исходных данных сенсоров.
в градусах/с. В дополнение для каждого сенсора определяется функция наблюдения h(xt), которая описывает, как вектор наблюдений zt вычисляется из исходных данных сенсоров.
Квадрокоптер измеряет свою горизонтальную 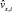 и
и 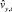 своих локальных координатах, которые трансформируются в глобальные
своих локальных координатах, которые трансформируются в глобальные  и
и 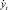 . Угол крена
. Угол крена 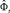 и тангажа
и тангажа 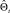 , измеряемые акселерометром, являются прямыми измерениями Φt и Θt соответственно. Для вычисления дрейфа рыскания производится дифференцирование измерения высоты
, измеряемые акселерометром, являются прямыми измерениями Φt и Θt соответственно. Для вычисления дрейфа рыскания производится дифференцирование измерения высоты  и рыскания
и рыскания 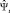 , и считаем их наблюдениями соответствующих скоростей. Следовательно, функцию наблюдения и вектор измерений можно записать как
, и считаем их наблюдениями соответствующих скоростей. Следовательно, функцию наблюдения и вектор измерений можно записать как
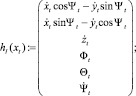 (2)
(2)
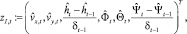 (3)
(3)
где δt обозначает время, которое прошло с момента t до момента t + 1.
Когда PTAM успешно отслеживает видеокадр, в первую очередь определяется масштаб положения квадрокоптера в пространстве через фактор масштаба λ* и преобразуется в систему локальных координат квадрокоптера, с использованием прямых наблюдений текущей позиции, которая задается как
hP(xt) := (xt, yt, zt, Φt, Θt, Ψt,)T; (4)
zP, t := f(EDC EC, t), (5)
где EC, t ∈ SE(3) является вычисленным положением камеры (масштабировано с λ); EDC ∈ SE(3) – статическое преобразование из координатной системы камеры в координатную систему квадрокоптера, и f:SE(3) → 6 преобразование из пространства SE(3) к представлению крен – тангаж – рыскание.
Модель предсказания показывает, как вектор состояния xt изменяется со временем. В частности, аппроксимируется горизонтальное ускорение квадрокоптера 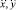 , основанное на текущем состоянии xt, и вычисляется вертикальное ускорение
, основанное на текущем состоянии xt, и вычисляется вертикальное ускорение  , ускорение вращения рыскания
, ускорение вращения рыскания 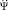 и скорость вращения по углам крена
и скорость вращения по углам крена  и тангажа
и тангажа  основанная на комбинации текущего состояния xt и активного управляющего состояния ut.
основанная на комбинации текущего состояния xt и активного управляющего состояния ut.
Горизонтальное ускорение пропорционально горизонтальной силе, действующей на квадрокоптер, задаваемой как
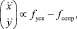 (6)
(6)
где fсопр обозначает тормозящую силу, а fуск ускоряющую. Сила сопротивления имеет линейную и квадратичную часть, соответствующую ламинарному и турбулентному потокам – задавая квадрокоптеру сравнительно небольшую скорость движения, мы можем аппроксимировать чистую линейную функцию к текущей горизонтальной скорости. Ускоряющая сила fуск пропорциональна проекции оси z квадрокоптера на горизонтальную плоскость. Вышесказанное можно представить как
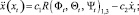 (7)
(7)
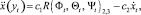 (8)
(8)
где R(•)i, j обозначает записи в матрице вращения, определенные углами крена, тангажа и рыскания.
Данная модель подразумевает постоянную тягу всех четырех роторов. Также аппроксимируется влияние отправляемых управляющих команд 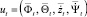 c помощью линейной модели:
c помощью линейной модели:
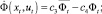 (9)
(9)
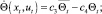 (10)
(10)
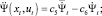 (11)
(11)
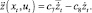 (12)
(12)
Коэффициенты c3…c8 определяются тестовыми полетами квадрокоптера. Общее состояние системы задается как
 (13)
(13)
Модель, описанная в формулах (7)–(13), не претендует на физическую правильность из за многочисленных допущений, но очень хорошо работает на практике, в основном за счет своей полноты: поведение всех параметров состояния и действие всех команд управления аппроксимируется, позволяя «слепой» прогноз, т.е. предсказание без наблюдений в течение короткого периода времени (~125 мс на практике).
Был произведен ряд экспериментов для анализа свойств полученной системы. Они проводились в различных средах – в помещениях различного размера и внешнего вида, а также на открытом воздухе под воздействием солнечных лучей и небольшого ветра.
Для анализа точности оценки масштаба квадрокоптеру было поручено пролететь заданную фигуру, в то же время каждую секунду брался образец данных и масштаб оценивался повторно. В первом тестовом наборе квадрокоптеру требовалось перемещаться только по вертикали, так как образцы данных в большей степени состояли только из измеренной высоты. Во втором наборе тестов квадрокоптеру требовалось пролететь горизонтальный прямоугольник, и в данном случае образцы данных состоят из измерений скорости при помощи встроенного IMU. После каждого полета мы измеряли истинную высоту  над поверхностью вручную, устанавливая квадрокоптер к двум точкам измерения и сравнивая известную дистанцию с измеренной системой визуальной навигации. Касательно первоначальной оценки значения
над поверхностью вручную, устанавливая квадрокоптер к двум точкам измерения и сравнивая известную дистанцию с измеренной системой визуальной навигации. Касательно первоначальной оценки значения  соотносятся со средней «глубиной» контрольных точек первого ключевого кадра, которая в наших экспериментах имела значение от 2 до 10 м. Для большего удобства сравнения, мы проанализировали и визуализировали ошибку
соотносятся со средней «глубиной» контрольных точек первого ключевого кадра, которая в наших экспериментах имела значение от 2 до 10 м. Для большего удобства сравнения, мы проанализировали и визуализировали ошибку 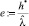 в соответствующую оцененной длине в 1 м.
в соответствующую оцененной длине в 1 м.
На рис. 3 представлена средняя ошибка, а также расхождение на протяжении 10 полетов. Как видено, наш метод быстро и точно определяет масштаб для двух типов движения квадрокоптера. В связи с повышенной точностью альтиметра в сравнении с измерением горизонтальной скорости, определение положения в пространстве происходит быстрее и точнее при вертикальном движении квадрокоптера, то есть схождение происходит через 2 секунды в сравнении с 15 секундами при горизонтальном движении, и финальная точность ±1,7 % в сравнении с ±5 %. Но в практическом применении мы рекомендуем использовать произвольные движения, что даст большее количество информации и значительно повысит точность и время сходимости.
Точность позиционирования. Также было произведено тестирование с точки зрения стабилизации положения квадрокоптера. Было задано удержание позиции квадрокоптером в течение 60 с в различных окружениях и измерена среднеквадратичная ошибка. Результаты представлены на рис. 3: измеренная ошибка находится между 4,9 см (внутри помещений) и 18 см (снаружи).
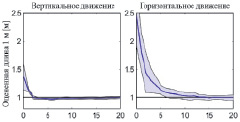

Рис. 3. Точность оценки расстояния и стабильность полета в различных окружениях
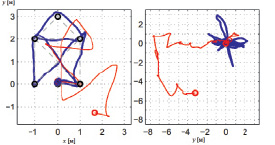
Рис. 4. Горизонтальная траектория полета квадрокоптера при выполнении полета по фигуре и удержании заданной позиции
Минимизация ухода измерений. Для проверки того, что визуальный SLAM минимизирует уход показателей одометрии, было произведено сравнение оцененной траектории с и без использования системы визуального SLAM. Рис. 4 показывает результирующие траектории с пролетом по фигуре и с удержанием заданной позиции, причем квадрокоптер был перемещен вручную с исходной позиции. Оба полета занимали около 40 с, и квадрокоптер был приземлен не более чем в 15 см от его исходного положения. В сравнении с исходными данными одометрии, накопленная ошибка составила 2,1 м для полета по фигуре и 6 метров для второго случая. Этот эксперимент демонстрирует то, что комбинирование визуального SLAM и инерциальных измерений эффективно минимизирует уход измерений положения во время совершения маневров.
Полеты по фигуре. Основываясь на точном определении положения и управлении, мы реализовали простой язык сценариев для полета по заданным траекториям. Команды включают в себя взлет, посадку и указание направления движения в координатах, начинающихся от места взлета. При помощи этого инструмента мы можем давать квадрокоптеру летать абсолютно автономно и выполнять различные маневры в рамках заданных команд.
Рецензенты:
Борзых В.Э., д.ф.-м.н., профессор, заведующий кафедрой информатики и информационных технологий, ФГБОУ ВПО «Тюменский государственный архитектурно-строительный университет», г. Тюмень;
Якубовский Ю.Е., д.т.н., профессор, заведующий кафедрой прикладной механики, ФГБОУ ВПО «Тюменский государственный нефтегазовый университет», г. Тюмень.



