Начиная с 1992 года ведется активная работа по изучению фотодетекторов, содержащих наноразмерные объекты в своей структуре (квантовые ямы, квантовые точки) [7, 14]. На данный момент эффективность таких структур не превышает 10 % [8], однако интерес к ним продолжает расти за счет технологических и электрофизических особенностей данных материалов. Наиболее изученными являются гетероструктуры с массивами квантовых точек InAs в матрице GaAs [1, 5]. Обнаружительная способность таких структур составляет порядка D* = 3·108 см·Гц1/2 при комнатной температуре [6]. Данные структуры, при межзонном поглощении, дают пик чувствительности в диапазоне 1,1–1,5 мкм [11], что удовлетворяет зоне ближнего ИК.
В данной работе предложена QD-InAs/GaAs гетероструктура для фотодетектора ближнего ИК-диапазона, на основании которой проведено моделирование спектров фотолюминесценции. Для проверки достоверности модели проведен сравнительный анализ результатов компьютерного моделирования с результатами сторонних исследовательских работ в данной тематике.
Теоретическое обоснование модели
Прежде чем перейти к описанию основных уравнений модели, необходимо сделать ряд допущений, связанных с различными подходами к моделированию структур на квантовых точках. Рассмотрим подробнее данные допущения.
1. После изучения ряда работ по раннему моделированию структур на квантовых точках [9, 12, 13] была выбрана пирамидальная форма квантовых точек в бесконечной полупроводниковой матрице.
2. Так как квантовые точки InAs являются центрами захвата электронов, справедливо, что неоднородность деформации не вносит изменений в энергетический спектр электронных состояний.
3. В предлагаемой модели рассматриваются только межзонные переходы. Соответственно, справедливо допущение, что в каждой квантовой яме, образованной квантовой точкой, содержится по одному дискретному уровню.
4. При моделировании использовался метод периодического потенциала Кронига – Пенни с учетом вклада влияния упругой деформации на эффективные массы носителей заряда.
Основные уравнения модели
Основополагающими уравнениями фотопреобразовательных структур являются уравнение Пуассона и уравнение непрерывности. Взяв закон Гаусса и Максвелла:
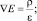
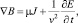(1)
где Е – энергия электрического поля; ρ – плотность носителей заряда; ε – диэлектрическая проницаемость материала; B – магнитное поле; µ – магнитная проницаемость; J – плотность тока; v – скорость света в среде, можно определить электрический потенциал в уравнении Пуассона и уравнение непрерывности.
Включив в уравнение непрерывности составляющие механизмов генерации и рекомбинации, получим уравнения непрерывности для электронов и дырок:
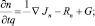
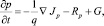(2)
где t – время; q – заряд электрона; n и p – концентрации электронов и дырок; Jn и Jp – плотности электронного и дырочного тока; Rn и Rp – скорости рекомбинации электронов и дырок; G – скорость генерации электронно-дырочных пар.
Как говорилось выше, квантовые точки в модели представляются в виде квантовых ям. Следовательно, мы будем иметь дело с двумерным электронным газом и уравнение для статистики распределения примет следующий вид:
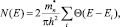(3)
где Θ – ступенчатая функция Хевисайда; h – постоянная Планка. Далее получаем двумерное выражение для концентрации электронов:
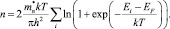(4)
Для учета локализации заряда по всей ширине квантовой ямы вводим соответствующую плоскую волновую функцию (выражение для направления оси роста структуры – х):
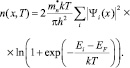(5)
Для дальнейшего решения необходимо знание зонной структуры (расположение валентной зоны и зоны проводимости), которое получается решением уравнения Шредингера с участием эффективных масс носителей заряда (ниже выражение для электронов):
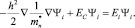(6)
Для моделирования зонной структуры была взята модель периодического прямоугольного потенциала Кронига – Пенни, модифицированная с условием действия равномерного поля деформации. Схематично модель прямоугольного потенциала изображена на рис. 1.
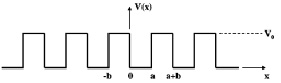
Рис. 1. Модель потенциала Кронига – Пенни
Модель потенциала представляет собой решение уравнения Шредингера в виде двух трансцендентных уравнений вида
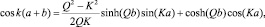E < V0; (7)
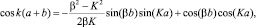E > V0, (8)
где K, Q, β – локальные волновые векторы:
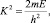V = 0, «E; (9)
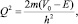V = 0, E < V0; (10)
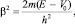V = 0, E > V0, (11)
Энергия определяется через волновой вектор функции Блоха:
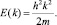(12)
Для моделирования спектров фотолюминесценции нами было выбрано стандартное выражение для излучательного потока [10].
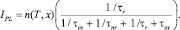(13)
где 1/τex – характеризует механизм перехода носителей заряда из зоны проводимости, в нашей модели выражен через туннельный эффект и термоэлектронную эмиссию; 1/τr – учитывает вклад излучательной рекомбинации; 1/τnr – вклад безызлучательной рекомбинации; 1/τex – вклад перехода носителей заряда на другие дискретные энергетические уровни в рамках одной потенциальной ямы (в данной модели не учитывается).
Для учета вклада термоэлектронной эмиссии воспользуемся моделью, описанной в [10] с некоторыми модификациями. Выражения для плотностей носителей заряда:
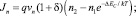
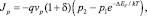(14)
где δ – коэффициент термоэлектронной эмиссии; vn и vp – скорости теплового движения электронов и дырок соответственно; ΔEC и ΔEV – различия энергий в зоне проводимости и валентной зоне.
Коэффициент термоэлектронной эмиссии:
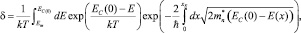(15)
где EC(0) – энергия в начальной точке потенциала; Em = max[EC(0), EC(W)] – максимальное значение энергии на всей ширине барьера (W).
Рекомбинация по модели Шокли – Рида – Холла учитывает ловушки захвата носителей заряда вблизи разрешенных зон. Обозначим через Nt плотность ловушек захвата, имеющих энергию Et в пределах ширины запрещенной зоны. В этом случае скорость рекомбинации будет иметь вид
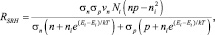(16)
где сечения захвата заряженных ловушек σn и нейтральных ловушек σp; ni – собственная концентрация носителей. Для удобства моделирования перепишем выражение (16) с учетом времени жизни носителей заряда:
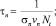
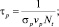(17)
(18)
Исходные данные для построения модели
Для построения модели была предложена гетероструктура с массивом InAs квантовых точек, изображенная на рис. 2.
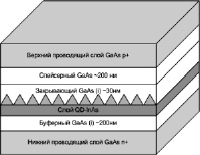
Рис. 2. Структура с массивом InAs квантовых точек
Моделируемая структура содержит слой GaAs с шириной запрещенной зоны 1,4 эВ и значением концентрации 3∙1017 см–3. Далее идет еще один слой GaAs толщиной 200 нм с подвижностью носителей заряда 8500 см2В–1с–1 (для электронов) и 400 см2В–1с–1 (для дырок). Следом слой InAs толщиной 3 монослоя и один массив квантовых точек InAs с поверхностной плотностью 1010 см–2 и латеральными размерами 35 нм. Далее два слоя GaAs, один толщиной 30 нм, второй толщиной 200 нм. Завершающий слой GaAs имеет значение концентрации 3∙1017 см–3.
Результаты исследования и их обсуждение
Зонная структура, рассчитанная по модели Кронига – Пенни, дала следующие результаты. За ширину потенциальной ямы были взяты размеры квантовых точек арсенида индия. Проведенные расчеты показали разницу энергий зоны проводимости между GaAs и InAs порядка 0,59 эВ. Расхождения значений эффективной массы у границ потенциальной ямы составили 0,024m0, а у границы барьера – 0,067m0. Различие энергии согласуется с теоретическими данными для структур подобного рода [12].
Результаты, полученные из зонной модели, были использованы для построений спектров фотолюминесценции. На рис. 3 представлены спектры фотолюминесценции рассматриваемой структуры в зависимости от температуры. Наблюдаются три пика зависимости, два из них в области среднего ИК-диапазона и один в коротковолновой области. Спектральный пик на длине волны 850 нм (I на графике) связан с рекомбинацией в слое GaAs. Интенсивность пика мала, что говорит о вкладе безызлучательных переходов и о малой доле проникающего излучения. Наибольшей интенсивностью обладает пик II (1080 нм), характеризующий основные переходы в массиве квантовых точек InAs. В нашей модели ширина пика составила 0,15 эВ при допущении однородности квантовых точек по размерам, однако на практике ширина и интенсивность пика основных переходов в квантовых точках могут отличаться, так как зависят от размеров квантовых точек. Пик III смещен в область длинных волн и характеризует вклад смачивающего слоя. При получении массива квантовых точек смачивающий слой представляет собой раствор GaxIn1-xAs. Оптимальным и наиболее изученным считается состав раствора с содержанием 35 % In [2, 3, 4, 15]. Разработанная модель дает пик смачивающего слоя на длине волны порядка 1,15 мкм, что соответствует ширине запрещенной зоны раствора Ga75In35As и согласуется с работами по получению структур подобного рода.
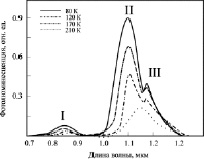
Рис. 3. Спектры фотолюминесценции
Стоит отметить, что все три пика имеют ярко выраженную зависимость от температуры. При увеличении температуры интенсивность пиков резко падает. Это говорит о преобладании процессов, связанных с температурой, повышается вероятность перехода носителей заряда за счет термоэлектронной эмиссии.
Проведя сравнительный анализ с работами [2, 4, 15], можно сказать, что выбранная модель дает достаточно корректные результаты и может быть доработана для сопоставления с экспериментальными данными. Интересно наблюдать, что в рассматриваемых работах по изучению спектров фотолюминесценции наблюдаются четыре пика активности. Четвертый пик, как правило, смещен в область среднего ИК и составляет 1,4–1,6 мкм. Данный спектральный отклик обусловлен присутствием квантовых точек большего латерального размера (дисперсия размеров массива квантовых точек).
Выводы
Предложена конструкция гетероструктуры (QD-InAs/GaAs) с массивом квантовых точек InAs для фотодетекторов ближнего ИК-диапазона. Разработана математическая модель построения зонной структуры и спектров фотолюминесценции на основании модели Кронига – Пенни и метода эффективных масс при межзонных переходах. Получены спектры фотолюминесценции с пиками интенсивности 1100 нм для основных межзонных переходов в квантовых точках, что говорит о возможности использования данной структуры в ближнем ИК-диапазоне. Установлено, что повышение температуры ведет к деградации эффективности структуры и сводится к нулю при комнатной температуре (300 К). Оптимальная температура для работы структуры составляет 77 К. Стоит отметить, что рассматриваемая структура с массивом квантовых точек при температуре 77 К имеет показатели эффективности выше, нежели другие наноструктуры (сверхрешетки, квантовые ямы и т.д.) [3]. Это говорит о перспективах дальнейшего изучения структур на квантовых точках и о возможности поднятия диапазона рабочих температур в перспективе до комнатной температуры.
Разработанная модель будет использоваться как основа для дальнейшего исследования внутризонных переходов в подобных структурах для фотодетекторов среднего и дальнего ИК-диапазонов.
Рецензенты:
Лунин Л.С., д.ф.-м.н., профессор, заведующий отделом, ФГБУН «Южный научный центр» Российской академии наук, г. Ростов-на-Дону;
Панич А.Е., д.т.н., профессор, директор – главный конструктор НКТБ «Пьезоприбор», Южный федеральный университет, г. Ростов-на-Дону.