В настоящее время развитие оптических систем передачи информации нового поколения основано на использовании широкополосных и сверхширокополосных сигналов. Воздействие аддитивных помех рассеяния можно минимизировать использованием методов нелинейной фильтрации, а влияние энергетического ослабления возможно компенсировать выбором энергетики оптического канала. В этой связи компенсация вредного влияния турбулентных неоднородностей среды распространения, создающих случайную пространственно-временную структуру показателя преломления и определяющих оптические свойства атмосферы, является наиболее сложной задачей.
Одним из наиболее эффективных способов ослабления возмущающего действия атмосферы является применение адаптивных методов и систем. Также можно отметить, что применение других методов и подходов в принципе не может обеспечить такого эффекта. Основные идеи, положенные в фундамент создания адаптивных систем, предложены сравнительно недавно. Процесс минимизации искажений волнового фронта в адаптивной оптической системе сводится к получению информации об искажениях, формированию управляющего воздействия на основе выбранных критериев и адаптации и коррекции фазового фронта. Адаптивные оптические системы фазовой компенсации в общем случае представляют собой систему автоматического управления с замкнутым многоканальным контуром. Основными элементами системы являются: анализатор – датчик фазового фронта, устройство обработки – цифровая или аналоговая ЭВМ и корректор фазового фронта. Существующие схемы функционирования адаптивных оптических систем позволяют решить задачу компенсации вредного влияния турбулентности. Получаемые при этом технические решения достаточно сложны. Поэтому существующие адаптивные оптические системы представляют собой многоканальные системы автоматического управления. А показатели качества таких систем в общем случае нелинейно зависят от числа каналов управления и улучшаются с их увеличением.
Для того чтобы адаптивные оптические системы передачи информации обеспечивали повышенную помехоустойчивость при минимальных аппаратурных затратах, число каналов необходимо ограничить при обеспечении заданного значения критерия качества. С экономической точки зрения для того чтобы адаптивные оптические системы передачи информации обеспечивали повышенную помехоустойчивость и как следствие – большую дальность действия при минимуме аппаратурных затрат, число каналов необходимо ограничить при обеспечении заданного значения критерия качества. Также к настоящему времени не решена задача синтеза специализированных алгоритмов оптимального и квазиоптимального измерения параметров фазового фронта в таких системах.
Основным элементом адаптивных оптических систем фазового сопряжения является датчик фазового фронта. С его помощью проводят измерения фазы в различных точках апертуры оптической системы с последующим «сшиванием» измерений и формированием распределения фазы фазового фронта по всему зрачку.
Датчики гартмановского типов позволяют измерять разности фаз между соседними участками апертуры или локальные наклоны фазового фронта, пропорциональные величинам вида, где k – волновое число; φ(x, y) – функция,
,
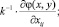
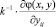описывающая распределение фазы на апертуре [1, 5].
Известен алгоритм [8] восстановления фазового фронта по результатам измерений частных производных в точках апертуры, предполагающий при обработке результатов измерений от т×п субапертур решение системы из (m + 1)(n + 1) линейных алгебраических уравнений. При решении такой системы не удается применить рекуррентную процедуру. При больших т и п это приводит к повышенным вычислительным затратам и ограничивает применение указанного алгоритма в реальном масштабе времени, а уменьшение т и п ведет к увеличению ошибки аппроксимации фазового фронта. В последнее время в технике адаптивной оптики возрос интерес к применению в качестве корректоров фазового фронта гибких зеркал с функциями отклика, близкими к ортогональным полиномам Цернике. При этом является актуальной задача вычисления управляющих сигналов для зеркал на современных ЭВМ с минимальными вычислительными затратами.
Цель работы – синтез алгоритма вычисления коэффициентов разложения фазового фронта по системе ортогональных полиномов на основе измерений значений частных производных фазового фронта в точках субапертуры.
Рассмотрим метод восстановления фазового фронта в виде разложения по системе ортогональных функций по результатам измерений датчика гартмановского типа.
Рассмотрим задачу в следующей постановке. Пусть на прямоугольной апертуре S размером (a, b)×(c, d), состоящей из т×п субапертур, датчик Гартмана измеряет значения частных производных вида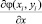 
и 
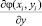в середине каждой субапертуры Sij. Зададим на интервалах (a, b) и (c, d) две системы ортогональных функций {μk(x)} и {λk(y)} 
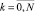из пространства C′(S), таких, что скалярные произведения вида
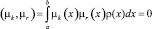при r ≠ k,
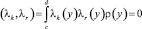при r ≠ k, (1)
и удовлетворяющих следующим дифференциальным уравнениям [8, 5]:
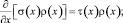
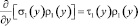(2)
при условиях
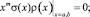
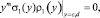(m = 0, 1, ...), (3)
где
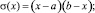
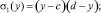
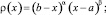
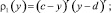
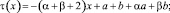
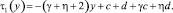
Искаженный фазовый фронт может быть представлен в виде [1, 3]:
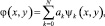(4)
где 
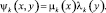(5)
Рассмотрим синтез алгоритма вычисления коэффициентов ak разложения вида (4) по результатам измерения значений частных производных фазового фронта в точках субапертуры. Продифференцируем по x и y выражение (4):
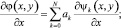
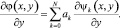(6)
Тогда значения частных производных фазового фронта в точках апертуры могут быть представлены как
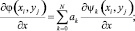
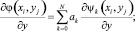(7)
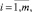
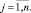
Коэффициенты ak получим из условия минимума функционала вида
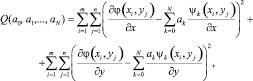
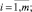
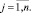(8)
Дифференцируя выражение (8) по a1 и приравнивая значения частных производных вида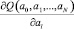 
к нулю, получим систему из N + 1 линейных уравнений:
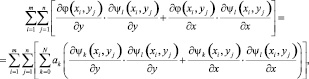(9)
N + 1 < m; N + 1 < n;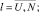 
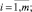
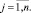
Введем следующие обозначения:
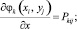
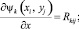
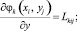
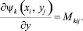
Учитывая свойство ортогональности производных полиномов, удовлетворяющих условиям(1), (2), (3), решение системы (9) запишется в виде
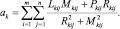(10)
В соответствии с формулой Родрига частные производные ортогональных полиномов могут быть представлены следующими соотношениями:
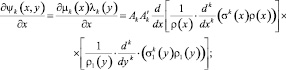(11)
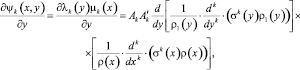(12)
где Ak,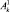 
– постоянные, зависящие от нормировки и определяемые по методике, изложенной в [1, 5]. Значения частных производных 
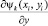и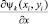 
для всех значений i, j, k могут быть рассчитаны заранее.
Для восстановления фазового фронта в соответствии с (10) потребуется P = 3Nmn операций. Функции отклика реальных зеркал могут не удовлетворять условиям (2), (3). Однако и в этом случае удается построить алгоритм восстановления фазового фронта.
Пусть в выражении (4) ψk не удовлетворяет (2), (3) и является функцией отклика гибкого зеркала. Тогда, введя обозначения
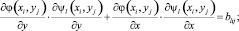
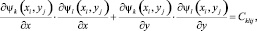
систему можно записать как
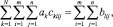
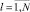(13)
или в матричной форме:
Da = F, (14)
где D – матрица правой части системы линейных уравнений (13) с элементами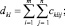 
a – вектор-строка искомых коэффициентов; F – вектор-столбец правой части системы с элементами
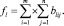
Решение системы запишется в виде
a = D–1F. (15)
Матрица D–1 для АОС вычисляется заранее, так как ее элементы не зависят от измеряемых датчиком гартмановского типа локальных наклонов фазового фронта на субапертурах. Таким образом, обработка результатов измерений фазового фронта в реальном масштабе времени сведется к вычислению элементов F в соответствии с (14) и умножению матрицы D–1 на F [7].
Выводы
Предложенный в работе метод позволяет существенно упростить конструкцию датчика фазового фронта и обеспечить его восстановление в реальном масштабе времени. Матрица D–1 может быть вычислена заранее, что также уменьшает объем вычислительных затрат. С учетом того, что на практике можно использовать ограниченное число полиномов, предложенный подход может быть использован в адаптивных оптических системах.
Рецензенты:
Звездина М.Ю., д.ф.-м.н., доцент, зав. кафедрой «Радиоэлектроника», ФГБОУ ВПО «Донской государственный технический университет», г. Ростов-на-Дону;
Габриэльян Д.Д., д.т.н., профессор, заместитель начальника научно-технического комплекса «Антенные системы» по науке, ФНПЦ ФГУП «РНИИРС», г. Ростов-на-Дону.