Одним из современных направлений развития промышленных систем управления является применение интеллектуальных материалов в измерительных и исполнительных элементах. К таким материалам относятся ферромагнетики с памятью формы (ФМПФ), способные изменять геометрические размеры под воздействием электромагнитных и механических сил и запоминать состояние [2, 5, 7]. Это позволяет повысить точность преобразования одного вида энергии в другой, упростить конструкцию устройств, сократить количество составных частей, подверженных поломке и износу. Как следствие, повысить эффективность систем управления. Поэтому разработка теории, принципов построения и средств исследования устройств на основе ФМПФ является актуальной задачей.
Постановка задачи
Целью работы является создание математической модели минимальной размерности и вычислительного алгоритма на ее основе для расчета магнитных полей актуаторов на основе ФМПФ. Полученные результаты могут быть использованы как при проектировании актуаторов, так и в задачах диагностики при прогнозировании состояния объекта и при анализе неисправностей в реальном времени.
Общий вид двухтактного актуатора показан на рис. 1 [6]. В нем используется распределенная намагничивающая система, содержащая n пар катушек без ферромагнитных сердечников, что позволяет повысить быстродействие, уменьшить массу и габариты устройства.
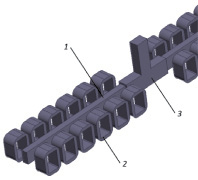
Рис. 1. Общий вид актуатора с двумя активными элементами (1), намагничивающими катушками (2) и исполнительным механизмом (3)
Математическая модель
Построим математическую модель магнитного поля одной пары катушек, между которыми находится часть активного элемента из ФМПФ, размеры которого совпадают с размерами окон катушек (рис. 2). Такую модель достаточно просто адаптировать на случай n пар катушек.
Стационарное трехмерное магнитное поле задачи описывается системой уравнений
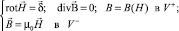 (1)
(1)
с граничными условиями на границе раздела сред: 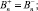
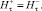 Здесь µ0 – магнитная постоянная;
Здесь µ0 – магнитная постоянная;  – плотность тока в катушках; V+ – подобласть, занятая активным элементом (ферромагнетиком); V– – подобласть, окружающего элемент пространства, заполненная линейной средой с µ0;
– плотность тока в катушках; V+ – подобласть, занятая активным элементом (ферромагнетиком); V– – подобласть, окружающего элемент пространства, заполненная линейной средой с µ0; 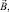
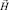 –магнитная индукция и напряженность магнитного поля соответственно;
–магнитная индукция и напряженность магнитного поля соответственно; 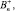
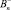 – нормальные составляющие магнитной индукции;
– нормальные составляющие магнитной индукции; 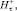
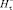 – тангенциальные составляющие напряженности магнитного поля на границе раздела сред V+ и V–.
– тангенциальные составляющие напряженности магнитного поля на границе раздела сред V+ и V–.
Для уменьшения размерности задачи будем далее использовать скалярный магнитный потенциал и фиктивные магнитные заряды. Это позволит применить для расчетов параметров поля в V– бессеточный численный метод фундаментальных решений (МФР).
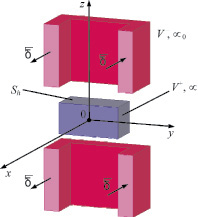
Рис. 2. Сечение исследуемой системы плоскостью y0z
Представим в V– напряженность магнитного поля в виде суммы двух полей [3]:
 (2)
(2)
где 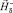 – напряженность магнитного поля, созданного токами катушек во всем пространстве V (V = V+ + V–) при удалении из V+ ферромагнетика;
– напряженность магнитного поля, созданного токами катушек во всем пространстве V (V = V+ + V–) при удалении из V+ ферромагнетика; 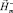 – напряженность магнитного поля в V–, созданного намагниченностью ферромагнетика при отсутствии тока в катушках.
– напряженность магнитного поля в V–, созданного намагниченностью ферромагнетика при отсутствии тока в катушках.
При использовании разложения (2) в V+ результирующее поле будет определяться как разность близких величин, что приведет к большим погрешностям. Поэтому, в отличие от [5], в V+ будем определять результирующее поле 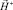 .
.
Исходную систему уравнений (1) после введения магнитного потенциала j заменим тремя системами:
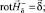
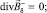
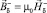 в V; (I)
в V; (I)
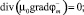
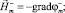
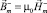 в V–; (II)
в V–; (II)
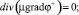
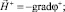 B = B(H) в V+. (III)
B = B(H) в V+. (III)
Решение системы (I) заменим вычислением 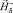 путем интегрирования по объемам катушек Vc (Vc = Vc1 + Vc2), используя формулу, полученную из закона Био – Савара – Лапласа [4]
путем интегрирования по объемам катушек Vc (Vc = Vc1 + Vc2), используя формулу, полученную из закона Био – Савара – Лапласа [4]
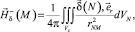 (3)
(3)
где 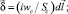 iwc – магнитодвижущая сила, создаваемая током i в катушке с числом витков wc; Sc – площадь сечения катушки;
iwc – магнитодвижущая сила, создаваемая током i в катушке с числом витков wc; Sc – площадь сечения катушки;  – единичный вектор, направленный из точки N к точке M.
– единичный вектор, направленный из точки N к точке M.
Решение системы (II) в V– выполним МФР, располагая в V+ фиктивные магнитные заряды.
Решение системы (III) в V+ с нелинейной средой из ФМПФ выполним методом конечных элементов (МКЭ).
Начало декартовой системы координат поместим в геометрическом центре активного элемента (рис. 2). Учитывая симметрию магнитной системы относительно плоскости x0y, будем решать задачу в области z ≥ 0. Принимаем, что на плоскости x0y все потенциалы 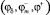 равны нулю. На боковых гранях параллелепипеда активного элемента положим
равны нулю. На боковых гранях параллелепипеда активного элемента положим 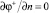 . На грани, лежащей в плоскости x0y, φ+ = 0. На верхней грани Sh имеем следующие соотношения, вытекающие из исходных граничных условий (1),
. На грани, лежащей в плоскости x0y, φ+ = 0. На верхней грани Sh имеем следующие соотношения, вытекающие из исходных граничных условий (1),
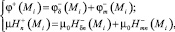 (4)
(4)
где 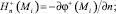
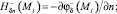
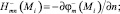
точка Mi ∈ Sh; i = 1, 2, ..., N; N – число точек коллокации на Sh.
Вычислительный алгоритм задачи
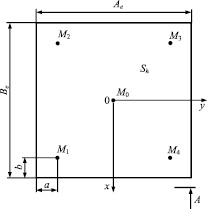
Считаем известными геометрические размеры активного элемента: ширину Ae и длину Be (размеры по осям 0x и 0y); толщину He (размер по оси 0z), геометрические размеры катушки (ширину Ac, длину Bc, толщину Hc, толщину намотки провода Cc) и магнитодвижущую силу iwc, создаваемую токами в катушках.
На верхней грани активного элемента разместим точки коллокации Mi (i = 1, 2, ..., N). Точки коллокации Mi имеют одинаковую z-координату 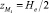 . Фиктивные магнитные заряды (количество их 2N) разместим в точках, x-координаты и y-координаты которых совпадают с соответствующими координатами точек коллокации Mi, причем
. Фиктивные магнитные заряды (количество их 2N) разместим в точках, x-координаты и y-координаты которых совпадают с соответствующими координатами точек коллокации Mi, причем 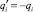 , что следует из равенства нулю потенциалов всех точек плоскости x0y.
, что следует из равенства нулю потенциалов всех точек плоскости x0y.
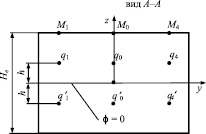
На рис. 3 показано положение точек коллокации M, при их числе N = 5, и фиктивных магнитных зарядов q, число зарядов 2N. Размеры a = b = 2∙10–3 м.
а
б
Рис. 3. Верхняя грань активного элемента Sh с точками коллокаций M(a) и расположением фиктивных магнитных зарядов q(b)
Аппликаты всех зарядов равны h для qi и –h для 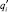 . Принимаем h = He/20.
. Принимаем h = He/20.
Потенциал в точке коллокации Mi определим по формуле [1]
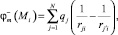 (5)
(5)
где 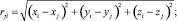
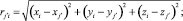
(xi, yi, zi) – координаты точки коллокации Mi; (xj, yj, zj) – координаты точки, в которой находится заряд qj; 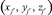 – координаты точки, в которой находится заряд
– координаты точки, в которой находится заряд 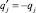 .
.
Z-составляющую напряженности магнитного поля в точке Mi, созданного зарядами, будем определять на основании (5) по формуле
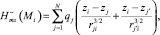 (6)
(6)
где zj = h; 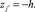
Система (4) с учетом соотношения (5) и (6) принимает следующий вид:
 (7)
(7)
Величина 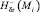 системы (7) определяется по формуле (3),
системы (7) определяется по формуле (3), 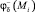 находиться из соотношения
находиться из соотношения
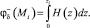 (8)
(8)
Таким образом, система (7), состоящая из 2N уравнений, содержит 3N неизвестных 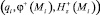 . Дополнительно N уравнений, связывающих φ+(Mi) и
. Дополнительно N уравнений, связывающих φ+(Mi) и 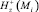 , получим, решая систему (III) МКЭ.
, получим, решая систему (III) МКЭ.
Алгоритм решения исходной задачи состоит из следующих этапов:
1. Выбираем расположения N точек коллокаций. Формируем массивы координат точек коллокации и точек, в которых расположены фиктивные магнитные заряды. Например, для точки Mi имеем Mi(xi, yi, H/2), qi(xi, yi, h), 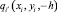 .
.
2. Вычисляем по формулам (3) и (8) в точках коллокации значения 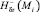 и
и 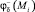 , i = 1, 2, ..., N.
, i = 1, 2, ..., N.
3. Учитывая, что 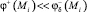 и
и 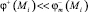 , полагаем φ+(Mi) = 0 и, решая первые N уравнений системы (7), найдем qi j = 1, 2, ..., N.
, полагаем φ+(Mi) = 0 и, решая первые N уравнений системы (7), найдем qi j = 1, 2, ..., N.
4. Решая вторые N уравнений системы (7), находим 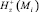 i = 1, 2, ..., N.
i = 1, 2, ..., N.
5. Решая краевую задачу МКЭ – систему (III) с граничными условиями: на Sh значения 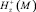 , где M ∈ Sh, в узлах конечной элементной сетки, которые определяются по второй формуле системы (7); на грани V+, лежащей в плоскости x0y, полагаем φ+ = 0, на боковых гранях
, где M ∈ Sh, в узлах конечной элементной сетки, которые определяются по второй формуле системы (7); на грани V+, лежащей в плоскости x0y, полагаем φ+ = 0, на боковых гранях 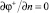 .
.
6. В тех случаях, когда магнитная проницаемость среды V+ зависит от H+, производится уточнение значений m и H+ с использованием зависимости B(H) ФМПФ.
7. Определив φ+(Mi), можно уточнить значения зарядов qi, решая систему (7).
Результаты экспериментальных исследований
Выберем для исследования систему (рис. 2), имеющую следующие параметры:
Ae = Be = Ac = Bc = 2∙10–3 м; He = 1∙10–3 м;
Hc = 2∙10–3 м; Cc = 0,5∙10–3 м.
Для оценки погрешности моделирования комбинированным методом (МФР и МКЭ) решим задачу МКЭ, при этом катушки и активный элемент поместим в центре параллелепипеда со сторонами 0,5×0,25×0,25 м, который заполним 87434 тетраэдрами. На гранях параллелепипеда задаем векторный магнитный потенциал 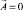 . На первом этапе расчетов определяем при iwc = 103. А каждой катушки значения
. На первом этапе расчетов определяем при iwc = 103. А каждой катушки значения 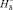 в точках коллокации Mi, а также в ряде точек на отрезке [0, zi], где zi = He/2. Далее численным интегрированием вычисляем
в точках коллокации Mi, а также в ряде точек на отрезке [0, zi], где zi = He/2. Далее численным интегрированием вычисляем 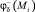 с использованием соотношения (8). Затем определяем величины
с использованием соотношения (8). Затем определяем величины 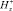 и φ+ в точках коллокаций.
и φ+ в точках коллокаций.
Перейдем к решению задачи комбинированным методом (МФР и МКЭ).
Вариант I. Выбираем N = 5 точек коллокаций (рис. 3). В силу симметрии их положения имеем q1 = q2 = q3 = q4. Таким образом, в этом варианте имеем два неизвестных заряда q0 и q1, а также 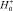 ,
, 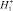 ,
, 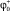 и
и 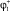 .
.
Величины 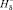 и
и 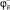 в точках коллокации M0 и M1 определяем по формулам (3), (8). В результате имеем систему уравнений
в точках коллокации M0 и M1 определяем по формулам (3), (8). В результате имеем систему уравнений
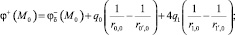
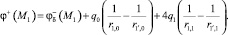
Полагая φ+(M0) = φ+(M1) = 0, найдем q0 и q1. Далее определяем H+(M0) и H+(M1) при начальном значении μ(0) = 103μ0. В случае μ(H+) решаем краевую задачу в V+ МКЭ, уточняя  φ+, q0, q1. Результаты сведем в табл. 1.
φ+, q0, q1. Результаты сведем в табл. 1.
Среднеквадратичное отклонение (RMSD) вычисляем по формуле
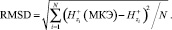
Таблица 1
Результаты расчетов при N = 5
|
Номер точки (i) |
Расчет комбинированным методом (МФР и МКЭ) |
Расчет МКЭ |
Относительная погрешность |
|||
|
|
|
|
φ+, А |
|
|
|
|
0 |
176613,4 |
83,8 |
445,8 |
0,1 |
266,2 |
67,4 |
|
1 |
125161,4 |
57,7 |
311,6 |
0,082 |
212,5 |
46,6 |
Относительное RMSD для N = 5 составило 53,3 %.
Вариант II. Разместим N = 13 точек коллокаций (рис. 4) на Sh. В силу симметрии положения точек имеем четыре неизвестных заряда q0, q1, q2, q3, а также неизвестные  и φ+(Mi), i = 0, 1, 2, 3.
и φ+(Mi), i = 0, 1, 2, 3.
Система уравнений составляется так же, как в варианте I. Результаты сведены в табл. 2. Относительное RMSD для N = 13 составило 9,1 %.
Замечание. Результаты, приведенные в табл. 1, 2, получены при μ = 103μ0.
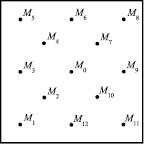
Рис. 4. Расположение точек коллокации N = 13
Таблица 2
Результаты расчетов при N = 13
|
Номер точки (i) |
Расчет комбинированным методом (МФР и МКЭ) |
Расчет МКЭ |
Относительная погрешность |
|||
|
|
|
|
φ+, А |
|
|
|
|
0 |
176613,4 |
83,8 |
306,5 |
0,089 |
266,2 |
15,1 |
|
1 |
125161,4 |
57,7 |
238,9 |
0,070 |
212,5 |
12,4 |
|
2 |
161570,5 |
69,5 |
233,0 |
0,099 |
238,0 |
–2,1 |
|
3 |
157664,0 |
74,0 |
265,1 |
0,055 |
246,4 |
7,6 |
Выводы
Предложена математическая модель минимальной размерности и алгоритм для расчета магнитного поля актуатора на основе ФМПФ. Модель и алгоритм основаны на разложении магнитного поля в линейной среде, окружающей устройство, на два поля: 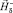 – напряженность магнитного поля, созданная токами катушек при отсутствии активного элемента из ФМПФ и поля
– напряженность магнитного поля, созданная токами катушек при отсутствии активного элемента из ФМПФ и поля 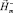 , создаваемого намагниченностью ФМПФ при отсутствии катушек с током. Для определения магнитного поля в окружающем пространстве
, создаваемого намагниченностью ФМПФ при отсутствии катушек с током. Для определения магнитного поля в окружающем пространстве 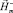 и активном элементе
и активном элементе 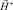 используются МФР и МКЭ соответственно. При этом магнитное поле
используются МФР и МКЭ соответственно. При этом магнитное поле 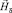 вычисляется по формуле, вытекающей из закона Био – Савара – Лапласа.
вычисляется по формуле, вытекающей из закона Био – Савара – Лапласа.
Достаточная для инженерных задач точность расчета параметров магнитного поля может быть получена при относительно небольшом числе фиктивных магнитных зарядов, что характерно для МФР [1]. Так при 26 зарядах погрешность расчета не превышает 9 %. Как следует из рис. 3, дальнейшее увеличение зарядов приведет к уменьшению погрешности. При 34 зарядах следует ожидать менее 5 %.
При учете симметрии магнитной системы размерность задачи существенно сокращается: при 10 зарядах число неизвестных равно двум (q0, q1), при 18 зарядах – трем (q0, q1, q2), при 26 зарядах – 4 (q0, q1, q2, q3). Это позволяет реализовать «быструю» компьютерную программу для расчета магнитных полей актуаторов на основе ФМПФ, что важно в задачах диагностики при прогнозировании состояния объекта и при анализе неисправностей в реальном времени.
Результаты работы получены при поддержке гранта РФФИ № 14-08-01288 «Разработка теории натурно-модельных испытаний измерительных и исполнительных систем, построенных на основе ферромагнитных материалов с эффектом памяти формы».
Рецензенты:
Савелов Н.С., д.т.н., доцент, профессор кафедры «Автоматика и телемеханика», ФГБОУ ВПО «Южно-Российский государственный политехнический университет имени М.И. Платова», г. Новочеркасск;
Седов А.В., д.т.н., доцент, профессор кафедры «Автоматика и телемеханика», ФГБОУ ВПО «Южно-Российский государственный политехнический университет имени М.И. Платова», г. Новочеркасск.




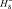 , А/м
, А/м
 , А
, А
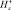 , А/м
, А/м
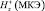 , А/м
, А/м
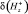 , %
, %
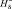 , А/м
, А/м
 , А
, А
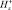 , А/м
, А/м
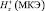 , А/м
, А/м
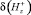 , %
, %