Для выходного и промежуточного контроля электромагнитных устройств ранее были разработаны ряд методов [12–14, 18, 19] и устройств [2, 3, 6, 8, 9, 11, 17]. В ходе проведенных работ были выявлены новые возможности диагностики неисправностей электромагнитных систем, основанные на анализе их вебер-амперных характеристик [7, 10, 15, 16]. При этом контроль магнитных свойств позволяет идентифицировать дефекты без необходимости проведения операций разборки/сборки изделий. Стоит отметить, что текущие электрические и магнитные характеристики и параметры привода несут в основном информацию о его состоянии в некоторый конкретный момент времени и не позволяют сделать вывод о появлении возможных неисправностей в предстоящий период эксплуатации. Более эффективными считаются системы прогнозирующей диагностики, в которых путем анализа результатов аналогичных контрольных операций за некоторый предыдущий период времени решается задача предсказания изменения состояния объекта в будущие моменты времени. Достижение данной важной цели требует выбора наиболее подходящих диагностических подходов и методов получения прогноза, учитывающих особенности объектов диагностирования. Применение методов прогнозирования принесет несомненную пользу: позволит определить время выхода из строя объекта и обосновать сроки профилактических работ, исключить «человеческий фактор» и ограничить количество персонала путем автоматизации процесса прогнозирования и определения состояния объекта на некоторый период времени вперед, сократить затраты на гарантийный ремонт и обслуживание путем выявления и оптимизации конструкции наименее отказоустойчивых элементов. Для постановки задачи прогнозирующей диагностики необходимо знать, на каких принципах может быть осуществлено ее решение, достигается ли цель путем применения известного математического аппарата, а также каким образом использовать известные подходы теории прогнозирования к данной предметной области.
Задача исследования состоит в определении оптимального метода прогнозирующей диагностики технического состояния электромагнитных приводов.
В качестве материалов используется теоретическое описание принципов работы предложенных ранее методов диагностики и прогнозирования технического состояния электромагнитных приводов, их достоинства и недостатки. Используемые методы: анализ, структурирование и алгоритмизация.
Описание методов прогнозирования технического состояния
При выборе метода прогнозирования необходимо учитывать следующие факторы: требуемая форма прогноза; горизонт, период и интервал прогнозирования; доступность данных; требуемая точность; поведение прогнозируемого процесса; стоимость разработки, установки и работы с системой; простота работы с системой. На практике наиболее удобно использовать первый принцип прогнозирования, так как он дает прогноз в той же размерности, что и измеряемая величина. При постановке задачи прогнозирования с позиции этого направления контролируемый процесс, характеризующий состояние объекта диагностики, представляется в виде многомерной функции yt, которая наблюдается дискретно или непрерывно в период времени t0 = 0 до tn в области T1, вследствие чего известны значения этой функции в соответствующие моменты времени yt1, yt2,…ytn. Задача прогнозирования заключается в определении величины заданной функции в будущие моменты времени ytn + 1, ytn + 2 и т.д. В этом случае рассматриваемая задача может быть решена различными методами.
Одним из наиболее простых является метод «наивных» моделей [5]. При создании таких моделей предполагается, что некоторый последний период прогнозируемого временного ряда лучше всего описывает будущее этого прогнозируемого ряда, поэтому в этих моделях прогноз, как правило, является очень простой функцией от значений прогнозируемой переменной в недалеком прошлом. Самой простой моделью является Y(t + 1) = Y(t), что соответствует предположению, что «завтра будет как сегодня». Такая модель не обладает высокой точностью, так как не учитывает механизмы, определяющие прогнозируемые данные, и не защищена от случайных флуктуаций.
Другим методом прогнозирования является метод среднего или скользящего среднего. Самой простой моделью, основанной на простом усреднении, является
Y(t + 1) = (1/(t))∙[Y(t) + Y(t – 1) + ... + Y(1)].
Этой модели соответствует принцип «завтра будет, как было в среднем за последнее время». Такая модель более устойчива к флуктуациям, поскольку в ней сглаживаются случайные выбросы относительно среднего. Несмотря на это, такой метод идеологически настолько же примитивен, как и «наивные» модели, и ему свойственны почти те же самые недостатки. В приведенной выше формуле предполагалось, что ряд усредняется по достаточно длительному интервалу времени. Однако, как правило, значения временного ряда из недалекого прошлого лучше описывают прогноз, чем более старые значения этого же ряда. Тогда можно использовать для прогнозирования скользящее среднее
Y(t + 1) = (1/(T + 1))∙[Y(t) + Y(t – 1) + ... + Y(t – T)].
Смысл его заключается в том, что модель видит только ближайшее прошлое (на T отсчетов по времени в глубину) и, основываясь только на этих данных, строит прогноз. При прогнозировании довольно часто используется метод экспоненциальных средних, который постоянно адаптируется к данным за счет новых значений. Формула, описывающая эту модель, записывается как
Y(t + 1) = α·Y(t) + (1 – α)Y·(t – 1),
где Y(t + 1) – прогноз на следующий период времени; Y(t) – реальное значение в момент времени t; Y(t – 1) – прошлый прогноз на момент времени t; α – постоянная сглаживания (0 ≤ α ≤ 1)). Модель простых средних:
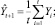
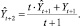
Модель скользящих средних:
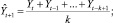
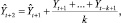
где k – порядок скользящих средних.
Если k = t, то получится метод простых средних, если k = 1, то наивный метод. Значит, таким методом, следует считать прогнозы, начиная с t = k.
Метод экспоненциального сглаживания:
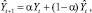
где α – сглаживающий параметр, определяющий зависимость прогноза от более старых данных, причем влияние данных на прогноз экспоненциально убывает с «возрастом» данных.
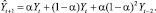
Все вышеприведенные модели хорошо работают, если тренд отсутствует.
В середине прошлого века Хольт предложил усовершенствованный метод экспоненциального сглаживания, впоследствии названный его именем. В предложенном алгоритме значения уровня сглаживаются с помощью экспоненциального сглаживания. Причем параметры сглаживания у них различны:
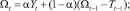
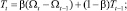
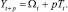
Здесь первое уравнение описывает сглаженный ряд общего уровня. Второе уравнение служит для оценки тренда. Третье уравнение определяет прогноз на p отсчетов по времени вперед. Постоянные сглаживания в методе Хольта идеологически играют ту же роль, что и постоянная в простом экспоненциальном сглаживании. Подбираются они путем перебора по этим параметрам с каким-то шагом. Можно использовать и менее сложные в смысле количества вычислений алгоритмы. Главное, что всегда можно подобрать такую пару параметров, которая дает большую точность модели на тестовом наборе, и затем использовать эту пару параметров при реальном прогнозировании. Частным случаем метода Хольта является метод Брауна, когда α = β.
Модель Хольта
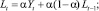
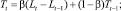
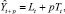
где p – просто число; α и β – выбираются как показатели точности. Обычно в зависимости от точности предыдущих прогнозов (чем больше средняя или еще какая-нибудь ошибка, тем больше эти параметры).
Для нахождения L применяется обратное прогнозирование обычно в зависимости от точности предыдущих прогнозов.
Модель Брауна
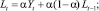
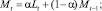
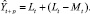
Хотя описанный выше метод Хольта (метод двухпараметрического экспоненциального сглаживания) и не является совсем простым (относительно «наивных» моделей и моделей, основанных на усреднении), он не позволяет учитывать случайные колебания при прогнозировании. Существует расширение метода Хольта до трехпараметрического экспоненциального сглаживания. Этот алгоритм называется методом Винтерса. При этом делается попытка учесть случайные колебания параметров. Система уравнений, описывающих метод Винтерса, выглядит следующим образом:
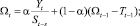
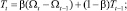
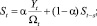
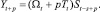
Дробь в первом уравнении служит для исключения случайной величины из Y(t). Полученный «чистый» прогноз, посчитанный по методу Хольта, умножается на случайный коэффициент.
Модель Винтерса
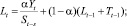
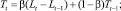
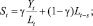
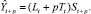
Наряду с описанными выше методами, основанными на экспоненциальном сглаживании, уже достаточно долгое время для прогнозирования используются регрессионные алгоритмы. Коротко суть алгоритмов такого класса можно описать так. Существует прогнозируемая переменная Y (зависимая переменная) и отобранный заранее комплект переменных, от которых она зависит – X1, X2, ..., XN (независимые переменные). Модель множественной регрессии в общем случае описывается выражением
Y = F(X1, X2....XN) + ε.
В более простом варианте линейной регрессионной модели зависимость зависимой переменной от независимых имеет вид
Y = β0 + β1X1 + .... + βN XN + ε,
где β0, β1, ..., βN – подбираемые коэффициенты регрессии, ε – компонента ошибки.
Предполагается, что все ошибки независимы и нормально распределены. Для построения регрессионных моделей необходимо иметь базу данных наблюдений. С помощью таблицы значений прошлых наблюдений можно подобрать (например, методом наименьших квадратов) коэффициенты регрессии, настроив тем самым модель. При работе с регрессией надо соблюдать определенную осторожность и обязательно проверить на адекватность найденные модели. Существуют разные способы такой проверки. Обязательным является статистический анализ остатков (тест Дарбина – Уотсона). Полезно иметь независимый набор примеров, на которых можно проверить качество работы модели.
Наиболее перспективным методом прогнозирования является использование нейронных сетей. Использование нейросетевой архитектуры и базы данных со всеми параметрами позволяет получить работающую систему прогнозирования. Причем учет или неучет системой внешних параметров будет определяться включением или исключением соответствующего входа в нейронную сеть. Дополнительным преимуществом нейронных сетей является то, что построение нейросетевой модели происходит адаптивно во время обучения, без участия эксперта, что исключает субъективные факторы. В настоящее время наиболее активно используются два основных типа моделей для нейросетевых методов прогнозирования: модели временных последовательностей и причинные модели. Временная последовательность – это упорядоченная во времени последовательность наблюдений (реализаций) переменной. Анализ временных последовательностей использует для прогнозирования переменной только исторические данные об ее изменении. Причинные модели используют связь между заданной временной последовательностью и одной или более другими временными последовательностями.
С учетом сложности и в первую очередь нелинейности объекта диагностики для проведения дальнейших исследований выбран метод прогнозирования на базе нейронных сетей и моделей временных последовательностей.
Обоснование подхода к прогнозирующей диагностике электромагнитных приводов путем анализа их вебер-амперных характеристик
В работах [10, 15, 16] представлен ряд доказательств, подтверждающий что появление дефектов электромагнитных приводов оказывает определенное влияние на форму вебер-амперной характеристики, в частности расположение в пространстве ψ(I) точек перегиба данной характеристики. В данной работе предполагаем, что положение данных точек изменяется в ходе жизненного цикла изделия и определяется постепенным проявлением дефекта изделия. Примером такого дефекта является изменение геометрии магнитной системы [16] в виде «скола» магнитопровода, препятствующего функционированию электропривода, в частности созданию необходимой силы перемещения F при некотором положении подвижного элемента x [4]. Окончательным проявлением данного дефекта на вебер-амперной характеристике будет снижение потокосцепления ψ при том же значении тока I. При этом в ходе развития дефекта магнитный поток также будет снижаться вследствие появления первичных трещин в магнитопроводе – дополнительных магнитных сопротивлений [1].
Стоит отметить, что сложность задачи прогнозирования времени развития дефекта заключается в неизвестном заранее для данного типа электропривода состоянии вебер-амперной характеристики, соответствующей наличию дефекта. Данная задача может быть успешно решена путем применения метода натурно-модельного эксперимента [19]. Обобщенный алгоритм решения задачи прогнозирования появления дефекта в управляемом электромагнитном приводе на базе искусственной нейронной сети представлен на рисунке.
Представленный алгоритм работает следующим образом. На первом этапе (рисунок, блок 1) производится экспериментальное определение вебер-амперной характеристики электромагнитного привода 
. Данный результат является входной величиной для проведения натурно-модельного эксперимента (НМЭ, рисунок, блок 2). Результатом выполнения НМЭ является адекватная компьютерная модель электропривода. На следующем этапе (рисунок, блок 3) выполняется изменение модели путем введения возможных изменений в электромагнитную систему привода (ЭМП) таким образом, чтобы представленное изменение проявилось в виде дефекта – отказа ЭМП. Полученные результаты фиксируются и передаются в блок настройки параметров искусственной нейронной сети (ИНС), прогнозирующей появление неисправности (рисунок, блок 4). Результатом настройки ИНС является некоторый набор параметров Θ. Данный набор параметров передается в блок программирования системы управления и диагностики электромагнитного привода (СУиД ЭМП, рисунок, блок 5).
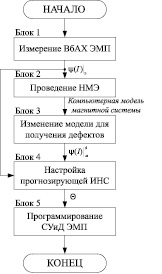
Обобщенный алгоритм решения задачи прогнозирования появления дефекта в управляемом электромагнитном приводе на базе искусственной нейронной сети
Заключение
В результате обзора и анализа методов диагностики электромагнитных приводов и математических принципов прогнозирования предложен принцип бессенсорной прогнозирующей диагностики на базе анализа изменения вебер-амперной характеристики во времени. Для определения вебер-амперной характеристики, соответствующей той или иной неисправности, предложено использовать натурно-модельный подход.
Результаты работы получены при поддержке гранта РФФИ № 15-38-20652 «Развитие теории бессенсорных прогнозирующих методов управления и диагностики электроприводов».
Рецензенты:
Горбатенко Н.И., д.т.н., зав. кафедрой «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск;
Кириевский Е.В., д.т.н., профессор кафедры «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск.