Современные промышленные предприятия нефтегазового комплекса представляют собой сложную техническую систему опасных производственных объектов, одним из элементов которой являются пожароопасные силовые масляные трансформаторы, техническое состояние которых влияет на непрерывность и безопасность технологических процессов. На предприятиях нефтегазового производства отказ силовых масляных трансформаторов может привести к созданию аварийных ситуаций, сопровождающихся значительным экономическим и экологическим ущербом. Для оценки технического состояния масляных трансформаторов в настоящее время применяется целый комплекс методов и средств, использующих различные диагностические параметры, одним из важнейших факторов, влияющих на надёжность функционирования силовых трансформаторов, является их эффективное охлаждение [1–2]. Существующие системы охлаждения силовых масляных трансформаторов имеют недостатки. Трансформаторное масло охлаждается с помощью радиаторов и вентиляторов крайне неэффективно.
В работах [7–13] предложена система охлаждения масляного трансформатора с применением всплывающих пузырьков газа. В качестве охлаждающего газа предлагается использовать элегаз, который характеризуется высоким коэффициентом теплового расширения и высокой плотностью. При высоком коэффициенте теплового расширения легко образуется конвективный поток, перераспределяющий тепловые потоки.
Измерение нестационарного температурного поля при наличии всплывающих пузырьков элегаза и их отсутствии позволяет определить эффективный коэффициент [3–5]. К сожалению, теории тепловых процессов, которая могла бы быть использована для определения коэффициента температуропроводности, нет.
Постановка задачи. Рассмотрим температурное поле в прямоугольном параллелепипеде, ограниченном по координатам x, y и z соответственно 0 < x < d/2, 0 < y < b/2, 0 < z < l.
При пропускании пузырьков элегаза [7–10], неравномерной нагрузке трансформатора и интенсивном теплообмене в среде обеспечить постоянство температуры на поверхности трансформаторного масла затруднительно. Температурное поле находится путем решения уравнения теплопроводности:
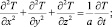
0 < x < d/2, 0 < y < b/2, 0 < z < l, t > 0. (1)
Начальное условие не изменяется:
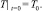 (2)
(2)
Предположим, что температура на поверхности трансформаторного масла зависит от времени по заданной зависимости, которая измеряется экспериментально:
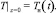 (3)
(3)
Для безразмерной температуры
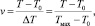
где Tmax – максимальная температура, математическую постановку задачи представим в виде
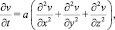
0 < x < d/2, 0 < y < b/2, 0 < z < l, t > 0; (4)
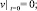 (5)
(5)
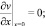
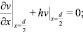
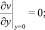
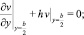 (6)
(6)
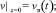
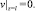
Решение задачи представим в виде свертки
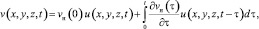 (7)
(7)
тогда задача для функции u примет вид
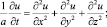 (8)
(8)
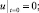 (9)
(9)
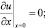
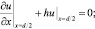 (10)
(10)
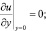
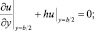 (11)
(11)
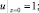
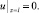 (12)
(12)
Решение задачи представляется в виде
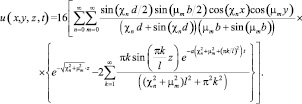 (13)
(13)
Окончательное выражение для температуры запишется в форме
 (14)
(14)
где χn и μm определяются из соответствующих трансцендентных уравнений:
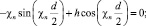
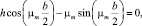
где n = 0, 1, 2,…, m = 0, 1, 2,…
Полученное решение задачи предназначено для определения эффективной теплопроводности, температуропроводности, коэффициента теплоотдачи, на основе результатов измерения температуры в созданной установке. Такая возможность обеспечивается на основе использования решений прямых задач в алгоритмах обратных задач на основе метода деления отрезка пополам и метода наименьших квадратов.
Для определения коэффициента температуропроводности трансформаторного масла с всплывающими элегазовыми пузырьками по экспериментальным значениям температуры созданы программы [6–7].
Анализ результатов. На рис. 1 представлен график зависимости стационарной температуры от вертикальной координаты z в центре резервуара x = 0 м, y = 0 м при различных значениях коэффициента теплообмена.
Как видно из рис. 1, температура воды при глубине меньше 0,1 м меняется по линейному закону с глубиной z, дальнейшее изменение температуры соответствует z > 0,1 м стремлению к температуре окружающей среды, что также подтверждено экспериментальными измерениями на установке. Анализ графиков позволяет выделить следующие три режима:
1) хорошая изоляция установки (температурное возмущение более 1 м);
2) средняя изоляция (температурное возмущение около 1 м);
3) слабая изоляция (температурное возмущение около 0,1 м).
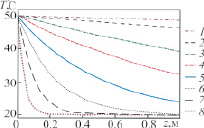
Рис. 1. Распределение стационарной температуры по глубине в центре резервуара при различных значениях параметра теплообмена h: 1 – 0,00005 м–1; 2 – 0,0005 м–1; 3 – 0,005 м–1; 4 – 0,02 м–1; 5 – 0,1 м–1; 6 – 0,5 м–1; 7 – 3 м–1; 8 –36,8 м–1
Как видно из рис. 2, с увеличением z температура воды уменьшается и стремится на больших глубинах к температуре окружающей среды. Обнаружены невысокие значения разницы температуры между центром и стенками резервуара при одинаковых значениях глубины z.
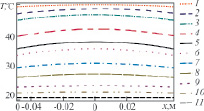
Рис. 2. Зависимости стационарной температуры от горизонтальной координаты x при y = 0 м, h = 6 м–1 для следующих глубин z: 1 – 0,001 м; 2 – 0,005 м; 3 – 0,01 м; 4 – 0,025 м; 5 – 0,04 м; 6 – 0,05 м; 7 – 0,075 м; 8 – 0,1 м; 9 – 0,15 м; 10 – 0,2 м; 11 – 0,5 м
Выводы
На основе решения задач о температурном поле произведены расчеты пространственно-временных зависимостей температуры применительно к масляным трансформаторам с элегазовым охлаждением и анализ произведенных расчетов.
Рецензенты:
Жирнов Б.С., д.т.н., профессор, заведующий кафедрой ХТП, филиал, ФГБОУ ВПО «Уфимский государственный нефтяной технический университет», г. Салават;
Вильданов Р.Г., д.т.н., профессор кафедры ЭАПП, филиал, ФГБОУ ВПО «Уфимский государственный нефтяной технический университет», г. Салават.



