Спасение жизней людей в экстренных ситуациях исчисляется минутами и даже секундами, в зависимости от стадии конкретного экстренного случая. Принятием наиболее оптимального решения в подобных ситуациях может быть минимизировано количество жертв. В данной работе рассматривается задача определения оптимального пути эвакуации в случае возникновения экстренных ситуаций внутри зданий, например пожар. Под оптимальным путем эвакуации при этом понимается наиболее безопасный и кратчайший маршрут от текущей позиции человека до выхода из здания. Для решения задачи построения такого маршрута в работе предложена модель, описывающая свойства потоков людей, перемещающихся в здании в случае эвакуации. Работа данной модели проверена на примере Петрозаводского государственного университета.
Анализ проблемы
В задачах эвакуации рассматриваются различные модели движения людей. Как правило, при решении задач эвакуации рассматривают сценарии поведения людей до чрезвычайной ситуации и после, когда начинается паника. Поведение людей в случае паники приводит к эффектам, подробно рассмотренным в работах [10, 11]:
● Затор – эффект «бутылочного горлышка». Данный эффект возникает в случаях, когда большое количество людей пытаются покинуть помещение через один выход. Заторы также возникают в случаях, когда два потока людей движутся через один проход навстречу друг другу и образуют противопотоки друг для друга.
● Раскачивание – данный эффект возникает при наличии противопотока. При прохождении одного человека через узкий проход за ним следует еще несколько, затем направление движения меняется, что и вызывает эффект раскачивания.
● Пересечение – возникает в случаях, когда различные потоки людей пересекаются друг с другом на перекрестках зданий, что замедляет процессы эвакуации. При строительстве зданий с целью сглаживания пересекающихся потоков в центре перекрестков зданий ставят препятствия округлой формы, что способствует сглаживанию пересечения потоков и организации кругового движения, как до возникновения чрезвычайной ситуации, так и после.
● Проложенный путь – эффект «хвоста», при котором часть людей следует за человеком, маршрут движения которого выглядит наиболее привлекательным, но не всегда является безопасным.
● «Быстрее значит медленнее» – данный феномен возникает в случае близкой опасности, когда люди максимально быстро устремляются к выходу, образуя давку и блокируя собой выход.
● Люди двигаются быстрее, чем до возникновения чрезвычайной ситуации; люди, находившиеся прежде в сидячем положении, при этом также становятся участниками движения.
● Увеличивается количество столкновений между людьми, что является следствием их падения и сдерживания при движении к выходу.
● Движения людей становятся нескоординированными.
● Эффект толпы, при котором люди делают то же, что и все, исключая при этом иные возможные пути эвакуации.
При построении оптимального маршрута в случае эвакуации необходимо учитывать обозначенные аспекты с целью их возможного исключения и уменьшения рисков возникновения пострадавших. В работе [12] авторы акцентируют внимание на том, что при эвакуации из горящего здания жертвами чаще становятся люди, которые не знакомы с конструкцией здания. Для нахождения оптимального пути авторы используют в своей работе алгоритм Дейкстры (Д), позволяющий определить кратчайший путь. Двери внутри здания представляют собой вершины, соединенные ребрами, и принимаются за исходные позиции. Каждое ребро имеет вес в виде расстояния. Безопасные выходы из здания представляют собой вершины назначения. Кратчайшие маршруты эвакуации строятся из каждой исходной вершины до соответствующей вершины назначения.
В случае применения алгоритма Д для решения задачи эвакуации недостаточно использовать в качестве весовых критериев ребер только расстояния. В работе [13] рассматривается модифицированный алгоритм Д для решения задачи эвакуации. В своей работе авторы не учитывают ребра, на участке которых есть опасность, исключая тем самым часть связей между рассматриваемыми вершинами. Маршрут эвакуации при этом строится уже на основе двух критериев – безопасности и протяженности.
Пожар является одной из экстренных ситуаций, требующих эвакуации людей из здания. Руководитель тушения пожара (РТП) в относительно простых случаях делает ошибочный выбор маршрута эвакуации людей в 27 % при среднем времени принятия решения 46 секунд. В сложных ситуациях данные значения возрастают [5]. В работе [5] также произведена сравнительная оценка реализации методов теории графов, теории игр и теории катастроф для решения задачи выбора оптимального пути. На основе результатов анализа наилучшим образом для решения данной задачи подходит теория графов. Также автором приведено сравнение наиболее часто используемых для решения данной задачи алгоритмов – Дейкстры (Д), Флойда ‒ Уоршелла (ФУ) и Беллмана ‒ Форда (БФ). Наилучшего результата, согласно представленному анализу, следует ожидать от алгоритма Флойда ‒ Уоршелла. Данный алгоритм помимо кратчайшего пути позволяет получить маршрутную информацию сразу для всех узлов сети. В своей работе автор рассматривает следующие критерии для корректировки маршрута: минимальное время движения, маршрут без огня, маршрут без теплового излучения. При использовании алгоритма ФУ маршрут корректируется с учетом указанных критериев.
В работе [9] также рассматриваются алгоритмы Д, ФУ и БФ для решения задачи эвакуации в шахтах. Наиболее эффективным для шахт является алгоритм Д. В то же время авторами отмечено, что алгоритм ФУ более эффективен, но менее прост, в связи с чем уступает алгоритму Д. Метод построения маршрута эвакуации из шахты в аварийной ситуации заключается в следующем [9]:
● Определение выработок, пригодных для осуществления аварийной эвакуации людей, и времени движения по ним с учетом геометрических (длина, площадь поперечного сечения, угол наклона), технологических (температура, влажность, количество технологического оборудования и промышленных отходов) и аварийных (возможное повышение температуры воздуха и избыток пожарных газов) характеристик.
● Формирование маршрутов аварийной эвакуации с наименьшим суммарным временем преодоления выработки.
● Проведение контрольных проверок оптимальных маршрутов.
Еще одним важным аспектом, влияющим на безопасность эвакуации, является наличие информации о скоплениях людей в какой-либо точке одного из маршрутов на момент возникновения чрезвычайной ситуации. Наличие подобной информации позволило бы формировать различные пути эвакуации для различных групп людей. В зданиях определить скопления людей можно при помощи методов локации объектов в помещениях на основе информации о WiFi-сигналах от мобильных устройств. Подобный подход предполагает наличие WiFi-сети в здании, для которого планируется определять маршруты эвакуации, и рассмотрен в работе [3].
Таким образом, при использовании алгоритмов построения оптимального маршрута эвакуации необходимо сформировать не только кратчайшие, но и безопасные для эвакуации маршруты. Безопасность маршрута в зависимости от типа объекта определяется дополнительными весовыми критериями, которые должны учитывать технологические и конструктивные особенности объекта, а также очаги опасности.
В Российской Федерации приказ МЧС России от 30.06.2009 № 382 допускает использование для расчетов трех моделей движения потоков людей: упрощенной аналитической, имитационно-стохастической и индивидуально-поточной. Для решения большинства инженерных задач наиболее эффективным инструментом является имитационно-стохастическая модель. Для моделирования сложных сценариев, учитывающих индивидуальные особенности людей, наиболее подходящей является индивидуально-поточная модель [4]. В данной работе представлена модель, наиболее подходящая для общих случаев, не учитывающая динамические свойства отдельных элементов потока.
Предлагаемая модель и способ решения
Рассмотрим в качестве модели здания связный граф G = (V, E), где V – множество вершин, E – множество ребер, E ⊂ V×V. Ребрам графа соответствуют части коридоров здания, вершинам графа – места разветвления коридоров или аудитории.
Пусть каждая вершина v ∈ V имеет неотрицательный вес wv, равный числу людей в соответствующем месте здания. Например, если вершина соответствует аудитории, то вес вершины – число находящихся в аудитории человек. Если в аудитории нет людей, то вес соответствующей вершины равен нулю. Веса частиц могут быть определены в процессе работы системы локации и подсчете числа людей в различных местах здания.
При движении людей по коридору здания целесообразно учитывать в расчетах допустимую плотность людского потока, определяя тем самым вес каждого ребра. В работе [8] людской поток D определяется как отношение количества людей в потоке N к площади занимаемого ими участка пути и измеряется в чел/м2. При этом участок имеет такие критерии, как ширину b и длину l:
D = N/(b⋅l). (1)
В зависимости от плотности авторами рассматриваются различные уровни комфортности людей, при этом экспериментально подтвержден физический предел плотности, составивший 14 чел./м2 при средней площади горизонтальной проекции людей, равной 0,09 м2/чел. (горизонтальной проекцией человека выступает эллипс, диаметры которого соответствуют ширине и толщине человека). Авторами также рассмотрено влияние вида пути на скорость движения потока при максимальных плотностях потока, которые составили 17 м/мин при движении по горизонтальному пути, 10 м/мин – по лестнице вниз и 8 м/мин – по лестнице вверх. Таким образом возможно рассчитать минимальную допустимую скорость эвакуации для ребер графа, соответствующих различным частям здания.
Пропускную способность ребра можно определить как отношение произведения площади соответствующего ребру коридора на плотность потока ко времени, необходимому на эвакуацию:
f = b⋅l⋅D/t, (2)
при этом время, необходимое на преодоление конкретного ребра, рассчитывается из исходя из его длины l и скорости движения человека. Далее предположим, что каждому ребру приписана пропускная способность, соответствующая количеству людей, которые могут пройти через соответствующий ребру коридор за время, назначенное на эвакуацию. Пусть задано подмножество вершин U ⊂ V, соответствующих местам выхода из здания.
В модели схему эвакуации людей из здания будем рассматривать как поток на графе. Поток определяет объемы перемещаемых по ребрам графа абстрактных частиц (людей в коридорах здания), находящихся в вершинах графа v ∈ V в объемах wv, и доставляющего его в вершины множества U (ниже будет представлено формальное определение потока). При этом в вершинах, не принадлежащих множеству U, после перемещения потока частиц не остается: число ушедших из вершины частиц равно сумме числа изначально имевшихся в вершине частиц (B на рис. 1) и числа пришедших в нее частиц (A и C). Данный поток можно интерпретировать как определение направлений движения эвакуируемых людей из аудиторий по коридорам здания к его выходам.
Летальный исход при концентрации окиси углерода CO в 1 % наступает за 2–3 минуты, двуокиси углерода CO2 – за 5 минут, снижение концентрации кислорода до 9 % также приводит к летальному исходу в течение 5 минут [8]. С учетом того, что время на эвакуацию в случае возникновения чрезвычайных ситуаций при наихудшем сценарии с момента возгорания составляет 2–5 минут, то для упрощения не будем рассматривать динамические по времени потоковые модели, а считать, что перемещение потока происходит в рамках неделимого на части периода времени.
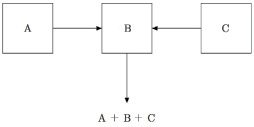
Рис. 1. Перемещение частиц в потоке
Будем рассматривать случай, когда при эвакуации запрещены разделения потоков людей. Тогда ребра графа с положительной величиной потока должны образовывать лес корневых деревьев с корнями из множества U. Лес корневых деревьев можно определить исходя из определения всех возможных путей эвакуации для каждого выхода из здания с учетом пропускной способности каждого ребра. Все пути в этом лесу идут в сторону корней деревьев.
Вернемся к построению модели. Будем считать, что если в графе имеется ребро {u, v}, инцидентное вершинам u и v, то множеству E принадлежат обе пары (u, v) и (v, u). Такое условие удобно тем, что порядок вершин в записи ребра однозначно определяет направление движения потока по ребру.
Обозначим Г(v) – множество вершин, смежных с вершиной v:
Г(v) = {u ∈ V | (u, v) ∈ E}, v ∈ V. (3)
Для каждого ребра (u, v) ∈ E заданы: tuv – расчетное среднее время, которое необходимо потратить человеку на прохождение соответствующего ребру коридора; fuv – пропускная способность, т.е. число людей, которые могут пройти по соответствующему ребру коридора за время tuv.
Будем полагать, что tuv = tvu, fuv = fvu для всех u, v ∈ E.
Дадим формальное определение потока. Пусть N – множество целых положительных чисел.
Определение. Поток – это функция x:E → N, которая каждому ребру ставит в соответствие целое положительное число, обладает следующими свойствами:
1. Ограничение на пропускную способность: 0 ≤ xuv ≤ fuv для всех u, v ∈ E.
2. Поток направлен по каждому ребру в одну сторону: xuv⋅xvu = 0 для всех u, v ∈ E.
3. Уравнение баланса:
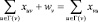для всех v∈V\U. (4)
4. Из каждой вершины поток «выходит» только по одному ребру:
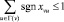для всех v ∈ V\U. (5)
5. Поток направлен в сторону выходов:
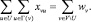(6)
Здесь обозначает значение функции x на паре (u, v). Добавим в модель учет времени на эвакуацию. Пусть
Гx(v) = {u ∈ Г(v) | xuv > 0}. (7)
Определим крайнее время эвакуации из точки, соответствующей вершине v ∈ V:
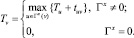(8)
Для всех v ∈ U должно быть выполнено ограничение: Tv ≤ T, где T – максимально допустимое время на эвакуацию людей из здания.
Недостаток модели – пока не учитывается, что время прохождения зависит от количества людей. Также все дальнейшие результаты в работе представлены без учета специфики эвакуируемых людей, например в работах [7, 6] авторы исследуют эвакуацию детей дошкольного возраста и инвалидов, эвакуация которых происходит гораздо медленнее, т.к. требуется помощь посторонних людей и/или обслуживающего персонала.
Примеры методов построения покрывающего корневого дерева рассмотрены в работах [1, 2]. Далее рассмотрим в качестве основного алгоритма, определяющего кратчайший путь эвакуации, алгоритм Д. В алгоритме Д кратчайший путь строится на основе информации о весах каждого ребра графа. В качестве весового критерия каждого ребра можно определить его пропускную способность, обратно пропорциональную единице (ребро с меньшим весом предпочтительнее). Чтобы удовлетворить условию уравнения баланса, для каждого выхода из здания необходимо рассчитать возможные пути эвакуации с учетом максимально допустимого количества людей в каждой вершине. Максимально возможное количество людей в вершине u будем рассчитывать исходя из пропускной способности ребра {u, v}:
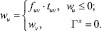(9)
При таком подходе пропускная способность каждого ребра всего пути эвакуации будет соответствовать пропускной способности ребра с самым низким значением:
fmin = min(fuv). (10)
Таким образом, достаточно определить ребро с минимальной пропускной способностью и далее рассчитать соответствующее каждой вершине максимально допустимое количество людей:
wu = fmin⋅tuv, (11)
Далее на основе информации о фактическом количестве людей в каждой вершине и полученных оптимальных путях до каждого выхода необходимо выбрать пути эвакуации с наименьшим временем, требуемым на их прохождение.
Экспериментальная площадка
В качестве экспериментальной площадки рассмотрен второй этаж главного корпуса Петрозаводского государственного университета. Процесс эвакуации можно разбить на три фазы:
1) люди находятся внутри комнат;
2) люди находятся в коридорах здания (покинули комнаты);
3) люди находятся на лестничной площадке (покинули коридоры).
а
б
Рис. 2. Фазы эвакуации: а – первая; б – вторая и третья
На рис. 2 представлена рассматриваемая тестовая площадка. Рис. 2 а соответствует первой фазе эвакуации. Вершины с номерами 1 по 10, отмеченные красным цветом, соответствуют лестничным площадкам с выходом из здания. До данных вершин предполагается расчет оптимальных маршрутов эвакуации. Позиции людей, соответствующие первой фазе эвакуации отмечены синими вершинами с номерами 11 по 92. На рис. 2 б представлены вторая и третья фазы эвакуации. В работе [7] рассматривается способ определения позиций мобильных устройств между двух базовых станций на примере того же здания. По результатам тестирования эмпирическим путем была подтверждена возможность достаточно точного определения позиций мобильных устройств относительно коридоров здания, что соответствует второй фазе эвакуации, в то время как фактические позиции могут соответствовать первой фазе. Таким образом, возможно допустить использование рассмотренного способа расчета локации в зданиях с вытянутой конструкцией, где переход из первой фазы эвакуации во вторую требует достаточно небольшого времени (менее минуты). Далее для расчетов оптимального маршрута эвакуации был использован граф с зелеными вершинами – номера с 1 по 74 на рис. 2 б.
Рис. 3. Пример вычисленных путей эвакуации
Результат расчета оптимальных путей
Рассмотрим результаты расчета оптимальных путей на примере ситуации, когда нужно эвакуировать людей из вершин 11–28, соответствующих второй фазе эвакуации, при условии, что узел 29 заблокирован (возгорание). На рис. 3 изображен результат расчета оптимальных путей эвакуации из каждой вершины и максимально допустимое количество людей, которые могут находиться на участках между различными вершинами с учетом пропускной способности каждого участка пути. Максимальное допустимое количество человек на каждом участке пути рассчитывалось с учетом описанных выше критических значений плотности потока (14 чел./м2), времени на эвакуацию (5 минут) и скорости движения в потоке по горизонтальному пути (17 м/мин). В качестве пояснения рассмотрим перемещение из вершины с номером 13 в вершину с номером 12. В данном случае на участке между данными вершинами не может находиться более 124 человек, время преодоления данного участка пути при этом составило 0,35 минуты.
Заключение
Предложенная в данной работе модель потока может быть использована для определения оптимальных путей эвакуации людей из здания. При эвакуации из сложных помещений на основе информации о позициях людей и их количестве в дальнейшем возможно включать аварийные сигналы выходов таким образом, чтобы избежать заторов в местах выходов, пересечений различных потоков людей, столкновений и, как следствие, возможных жертв. При расчете допустимого количества людей необходимо учитывать критические значения плотности потока и скорости его движения, на основе чего можно вычислить пропускную способность каждого участка пути эвакуации, для дальнейшего использования ее в качестве весового критерия при определении оптимального пути. Предложенная модель потока не учитывает индивидуальные особенности различных групп людей и применима в случаях, когда определено предельно допустимое время эвакуации.
Исследования, описанные в статье, поддерживались Петрозаводским государственным университетом (Программа стратегического развития ПетрГУ на 2012–2016 гг.).
Рецензенты:
Рогов А.А., д.т.н., профессор кафедры теории вероятности и анализа данных, Петрозаводский государственный университет, г. Петрозаводск;
Печников А.А., д.т.н., доцент, ведущий научный сотрудник, Институт прикладных математических исследований Карельского научного центра РАН, г. Петрозаводск.