Навигационная безопасность коллективного движения судов является актуальной проблемой эксплуатации водных транспортных путей [9]. Её обеспечение возложено на береговые системы управления движением судов (СУДС). Их информационной базой являются радары и транспондеры Автоматической идентификационной системы (АИС) [10].
Определение судов, чьё движение является потенциально опасным (ведёт к столкновению), и выработка тревожных сигналов является центральной функцией, реализующей целевое назначение СУДС. Число объектов, для которых в текущий момент времени может быть выработан тревожный сигнал, увеличивается с ростом интенсивности движения [1]. Это является побудительным мотивом дополнительно учитывать тип навигационной ситуации и выделять различные уровни опасности (типа «очень опасная», «опасная», «почти безопасная» и т.п.) [8].
Настоящая статья посвящена изучению модели задачи предупреждения об опасном сближении типа «судно ‒ берег». Несмотря на то, что этой теме посвящено достаточно много публикаций [4], она продолжает оставаться актуальной для практики. Наличие случайной компоненты, обусловленной инструментальной погрешностью измерений, предопределяет выбор для распознавания опасных ситуаций моделей вероятностного типа.
Модельные представления задачи
Пусть измеряемыми параметрами являются декартовы координаты объекта. Будем описывать эволюцию координат объекта простейшими полиномиальными моделями. Целью решения задачи является определение вектора оценок 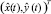 . В силу вероятностного характера значений оценок вектор
. В силу вероятностного характера значений оценок вектор 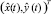 имеет смысл только вместе с информацией о характеристиках случайных погрешностей оценивания (величинах
имеет смысл только вместе с информацией о характеристиках случайных погрешностей оценивания (величинах 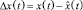 ,
, 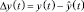 ).
).
Разделим наблюдаемую акваторию на две зоны: участок, где движение судов возможно без ограничений (разрешённую зону, множество Y), и участок, где движение судов запрещено (запрещённую зону, множество N). Определим корабельный домен [12, 13] S° в виде круга радиуса R°, очерченного вокруг условной точки – центра судна. Будем трактовать этот домен в статическом смысле – как зону, вторжение в которую интерпретируется как опасность. В таком случае за опасную ситуацию можно принять факт наличия (в данный момент времени) непустого пересечения множеств N и S°.
Пусть положение наблюдаемого объекта в данный момент времени t характеризуется оценкой его координат – вектором 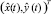 и функцией плотности распределения вероятностей оценок f(x, y). Опишем возможные способы определения понятия «вероятность опасной ситуации».
и функцией плотности распределения вероятностей оценок f(x, y). Опишем возможные способы определения понятия «вероятность опасной ситуации».
1. Рассмотрим разрешённую зону Y. В её рамках выделим зону Y* – множество разрешённых положений центра судна (т.е. приведём Y к Y* с учётом радиуса корабельного домена (рисунок а). Если 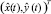 – оценка положения центра объекта, а f(x, y) – функция плотностей распределения вероятностей оценок, то вероятность того, что (x(t), y(t))T ∈ Y* (т.е. корабельный домен в момент времени t лежит в безопасной зоне) может быть найдена по формуле
– оценка положения центра объекта, а f(x, y) – функция плотностей распределения вероятностей оценок, то вероятность того, что (x(t), y(t))T ∈ Y* (т.е. корабельный домен в момент времени t лежит в безопасной зоне) может быть найдена по формуле
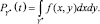 (1)
(1)
2. Как и в первом случае, приведём зону Y к Y*. Пусть 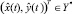 . Обозначим через ρ минимальное расстояние от
. Обозначим через ρ минимальное расстояние от 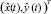 до границы Y* и введём понятие круга безопасности объекта
до границы Y* и введём понятие круга безопасности объекта 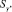 – круга с центром
– круга с центром 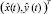 и радиусом ρ (рисунок, б); как видно из рисунка,
и радиусом ρ (рисунок, б); как видно из рисунка, 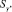 не следует отождествлять с корабельным доменом S°). Вероятность того, что
не следует отождествлять с корабельным доменом S°). Вероятность того, что 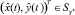 (т.е. центр судна в момент времени t лежит в круге безопасности) может быть найдена по формуле
(т.е. центр судна в момент времени t лежит в круге безопасности) может быть найдена по формуле
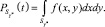 (2)
(2)
В случае, когда 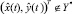 , примем
, примем 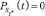 .
.
3. Рассмотрим вектор оценок координат объекта 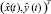 и зону Y*. Пусть
и зону Y*. Пусть 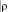 – минимальное расстояние от точки
– минимальное расстояние от точки 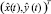 до границы Y*, причём ρ > 0, если
до границы Y*, причём ρ > 0, если 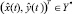 , и ρ < 0, если
, и ρ < 0, если 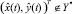 (рисунок, в). Если f(ρ) – функция плотности распределения вероятностей случайной величины ρ (вероятностный характер которой обусловлен статистикой
(рисунок, в). Если f(ρ) – функция плотности распределения вероятностей случайной величины ρ (вероятностный характер которой обусловлен статистикой 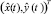 ), то вероятность того, что ρ > 0 в момент времениt (то есть центр объекта лежит в зоне Y*) можно определить по формуле
), то вероятность того, что ρ > 0 в момент времениt (то есть центр объекта лежит в зоне Y*) можно определить по формуле
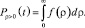 (3)
(3)
Величины 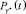 ,
, 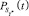 и
и 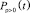 можно интерпретировать как вероятности безопасной ситуации в момент времени t (безопасного положения судна по отношению к берегу). Соответственно, величины
можно интерпретировать как вероятности безопасной ситуации в момент времени t (безопасного положения судна по отношению к берегу). Соответственно, величины 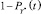 ,
, 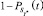 и
и 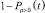 можно принять в качестве вероятностей опасной ситуации.
можно принять в качестве вероятностей опасной ситуации.
Метод решения задачи
Предлагаемый метод оценки вектора состояния задачи связан с её сведением к конечномерному виду задачи метода наименьших квадратов. Применение метода наименьших квадратов даёт возможность достаточно просто определить функцию плотности распределения вероятности координат объекта f(x, y). Так, можно показать, что в этом случае f(x, y) близка к плотности двумерного нормального распределения со средним (x(t0), y(t0))T и дисперсиями 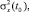
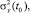
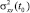 , соответствующими дисперсионной матрице задачи.
, соответствующими дисперсионной матрице задачи.

а б в
Иллюстрация понятий, используемых при моделировании опасной ситуации для случая «судно ‒ берег»
Будем разделять наблюдаемые объекты на два класса: движущиеся прямолинейно и равномерно и маневрирующие. Предлагается следующий алгоритм выделения маневрирующих объектов. Пусть 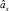 ,
, 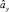 и
и 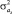 ,
, 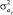 – значения оценок ускорений объекта и их дисперсий, вычисленные методом наименьших квадратов. Тогда вероятность того, что нулевые значения ускорений ax, ay не входят в область их вероятных значений, может быть определена формулами
– значения оценок ускорений объекта и их дисперсий, вычисленные методом наименьших квадратов. Тогда вероятность того, что нулевые значения ускорений ax, ay не входят в область их вероятных значений, может быть определена формулами
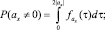
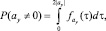 (4)
(4)
где 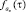 ,
, 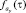 – функции плотностей нормального распределения со средними
– функции плотностей нормального распределения со средними 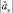 ,
, 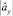 и дисперсиями
и дисперсиями 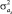 ,
, 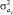 . Решение о том, что объект является маневрирующим, принимается в том случае, если значение
. Решение о том, что объект является маневрирующим, принимается в том случае, если значение 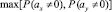 превышает некоторый порог. В противном случае принимается решение о неопределённой ситуации.
превышает некоторый порог. В противном случае принимается решение о неопределённой ситуации.
Определим следующие вербальные уровни опасности для объекта. Под ситуацией с уровнем опасности «красная тревога» (RED) будем понимать ситуацию, когда возникновение опасности возможно без изменения текущих курса и скорости движения. Ситуацией с уровнем опасности «желтая тревога» (YELLOW) назовём ситуацию, когда возникновение опасности имеет место при маневрировании судна. Наконец, уровнем «отсутствие тревоги» (GREEN) будем называть случай, когда возникновение опасности маловероятно при любом типе движения [7, 11, 2].
Введём величины 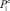 ,
,  , определяемые в зависимости от типа объекта:
, определяемые в зависимости от типа объекта:
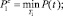
– для объектов, движущихся прямолинейно и равномерно, и
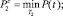
– для маневрирующих объектов. Здесь T1, T2 – время прогнозирования траектории для модели соответствующего порядка; P(t) – вероятность безопасной ситуации, определяемая как (1), (2) или (3).
В соответствии с описанными модельными представлениями предлагается следующая дискретная система правил соотнесения уровней опасности с вычисленными значениями вероятностей 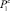 и
и 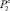 (таблица). Здесь p* – некоторый порог безопасности, с которым сравниваются значения
(таблица). Здесь p* – некоторый порог безопасности, с которым сравниваются значения 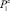 ,
,  ; d – значения детектора маневра, причём d = 1, если манёвр зафиксирован, и d = 0 в случае неопределённой ситуации; «GREEN», «YELLOW», «RED» – соответствующие вербальные значения уровня опасности.
; d – значения детектора маневра, причём d = 1, если манёвр зафиксирован, и d = 0 в случае неопределённой ситуации; «GREEN», «YELLOW», «RED» – соответствующие вербальные значения уровня опасности.
На практике определение в условиях внешнего наблюдения по конкретному судну уровня «GREEN» означает, что его движение не представляет опасности; уровня «YELLOW» означает, что опасная ситуация возможна, но при этом судно маневрирует, то есть судоводитель, скорее всего, сам контролирует ситуацию и старается придать движению безопасный характер; уровня «RED» – движение судна ведёт к опасности и необходимо начать манёвр уклонения [3–6].
Система правил определения уровня опасности в задаче «судно ‒ берег»
|
№ п/п |
|
|
d |
GREEN |
YELLOW |
RED |
|
1 |
+ |
+ |
1 |
+ |
||
|
2 |
+ |
+ |
0 |
+ |
||
|
3 |
+ |
– |
1 |
+ |
||
|
4 |
+ |
– |
0 |
+ |
||
|
5 |
– |
+ |
1 |
+ |
||
|
6 |
– |
+ |
0 |
+ |
||
|
7 |
– |
– |
1 |
+ |
||
|
8 |
– |
– |
0 |
+ |
Заключение
Рассмотренный в статье подход к решению задачи предупреждения об опасном сближении судов позволяет наглядно представлять особенности навигационной обстановки. Предложенная цветовая интерпретация уровней тревоги типа «красный» и «желтый» интуитивно понятна судоводителям и операторам СУДС.
Результаты работы ориентированы на расширение функций современных систем управления движением судов.
Рецензенты:
Игнатюк В.А., д.т.н., профессор кафедры информационных технологий и систем, Владивостокский государственный университет экономики и сервиса Минобразования РФ, г. Владивосток;
Кривошеев В.П., д.т.н., профессор кафедры информационных технологий и систем, Владивостокский государственный университет экономики и сервиса Минобразования РФ, г. Владивосток.





