Модели динамики биологических популяций являются одним из ключевых инструментов современной экологии, биофизики биологических сообществ, популяционной биологии. Особый интерес представляют модели пространственно распределенных сообществ с миграциями. Мы будем рассматривать модели динамики популяции на основе принципа эволюционной оптимальности [1–4], в которых перемещения особей носят целенаправленный характер и должны максимизировать средний по пространству коэффициент размножения (КР). Будем предполагать, что особи глобально информированы и могут реализовывать рефлексивную стратегию перемещения из стации в стацию. Глобальная информированность означает, что особям известна вся информация о состоянии окружающей среды в месте их пребывания, а также в стации эмиграции, информация о численностях субпопуляций в обеих стациях и цена перемещения (т.е. затраты на перемещение из стации в стацию, выраженные в долях КР). Под рефлексивным поведением будем понимать миграционное поведение особей, которое зависит от миграционного поведения нерефлексирующих особей. Нерефлексирующие особи руководствуются в своем миграционном поведении только параметрами окружающей среды и плотностью субпопуляции в стациях. Выясним, оказывает ли влияние рефлексивное поведение особей на численность популяции. Для этого сравним динамику численности для модели глобально информированных особей без рефлексивного поведения и динамику численности для модели глобально информированных особей с рефлексивным поведением. Рассмотрим также два варианта размножения. Первый вариант – считается, что все особи, не зависимо от информированности, относятся к одному виду. Второй вариант – особи разной информированности будут рассматриваться как подвиды исходного вида.
Модель глобально информированных особей без рефлексивного поведения
Будем рассматривать сообщество, состоящее из одного вида, особи в котором распределены по двум стациям. Ситуацией миграции будем считать перемещение особей из одной стации в другую. Все остальные перемещения внутри стаций, в реальной ситуации неизбежные, миграцией считаться не будут. Будем рассматривать динамику в дискретном времени.
Пусть динамика сообщества в каждой из стаций (в отсутствие миграции) описывается уравнением Ферхюльста
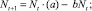
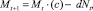(1)
где Nt(Mt) – численность особей в момент времени t в I (соответственно, во II стации); a и c описывают плодовитость, b и d описывают плотностно зависимые факторы саморегуляции. Функции, стоящие в скобках, будем называть коэффициентами размножения (КР) соответственно в первой и второй стации.
Определим условия миграции. Миграция из стации в стацию происходит в том и только в том случае, когда условия существования в стации иммиграции оказываются лучше, чем в стации пребывания, с учетом цены перемещения p. Величина p (0 < p ≤ 1) описывает вероятность перемещения из стации в стацию без ущерба для дальнейшего размножения.
Условие наличия миграции из стации I в стацию II (соответственно из II в I):
(
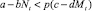
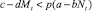,соответственно). (2)
Перемещается такое количество особей Δ, которое обращает неравенство (2) в равенство. Очевидно, что Δ ≤ Nt (либо Δ ≤ Mt). Если на шаге t миграция происходит, то Δ определяется одним из двух соотношений:
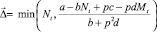
либо
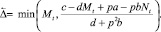(3)
Модель (1)–(3) необратима по времени: операция, соответствующая акту миграции, является проектированием. Отметим, что в данной модели миграционный поток однонаправлен. Встречных потоков миграции быть не может.
Еще раз коротко опишем, как работает модель. На каждом шаге времени t проверяются условия возникновения миграции, вычисляется величина миграционного потока Δ и происходит перераспределение особей по стациям. Вычисляются новые численност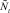и 
и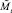 
по следующим формулам:
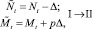
или
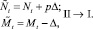(4)
Для полученных численностей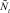 
и 
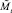вычисляются численности на шаге t + 1 по формуле (1).
Модель глобально информированных особей с рефлексивным поведением
Перейдем теперь к описанию модели с рефлексивным поведением. Под рефлексивным поведением мы будем понимать такое, при котором одна из сторон конфликта (или взаимодействия) предугадывает или прогнозирует поведение противоположной стороны. Базовые подходы к описанию и моделированию такого поведения были разработаны В.А. Лефевром [5].
Будем предполагать, что популяция у нас делится на два подвида: рефлексирующих особей Rt и нерефлексирующих особей NRt, которые могут быть распределены по обеим стациям. Считаем, что на начальном шаге по времени каждый из подвидов занимает свою стацию, например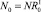 
, 
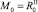. На следующих шагах по времени численности в стациях являются суммой численностей рефлексирующих и нерефлексирующих особе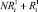й: 
и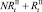 
. Модель при этом меняется следующим образом. Проверяются условия наличия миграции для общих численностей в стациях:
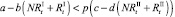
или
.
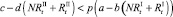Если какое-то из условий выполнено, определяется величина миграционного потока Δ и происходит миграция нерефлексирующих особей. В случае, если миграционный поток по величине больше, чем численность нерефлексирующих особей в данной стации, то величина миграционного потока приравнивается к количеству таких особей в стации. После этого вычисляются численност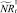и 
и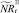 
:
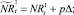
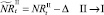
или
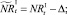
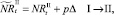
которые сложатся в результате миграции нерефлексирующих особей на данном шаге. Для этих численностей снова проверяются условия существования миграции:
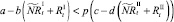
или
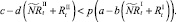
В случае если какое-то из условий выполняется, вычисляется величина миграционного потока Δ для рефлексирующих особей и происходит перераспределение по стациям уже этих особей, то есть вычисляются новые численност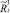и 
и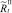 
:
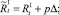
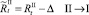
или
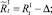
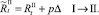
Численности на шаге t + 1 вычисляются следующим образом:
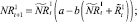
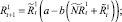
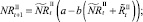
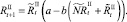
То есть численности нерефлексирующих и рефлексирующих особей на шаге t + 1 зависят от общей численности особей в стациях.
Мы также рассматриваем случай, когда рефлексирующие и нерефлексирующие особи при размножении представляют собой отдельные подвиды. В этом случае численности на шаге t + 1 вычисляются по следующим формулам:
|
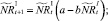
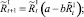
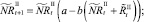
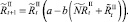
p |
SN, % |
SNR, % |
SNRO, % |
SRavn, % |
SS, % |
|
0,1 |
8,80934 |
13,8686 |
71,5804 |
5,64206 |
0,0996 |
|
0,2 |
3,43894 |
16,6697 |
74,4578 |
5,31491 |
0,118576 |
|
0,3 |
1,80178 |
21,8464 |
71,6109 |
4,61678 |
0,12416 |
|
0,4 |
1,35586 |
27,7823 |
66,7888 |
3,9427 |
0,130352 |
|
0,5 |
1,50704 |
29,9224 |
65,0931 |
3,33198 |
0,145536 |
|
0,6 |
1,89078 |
27,5213 |
68,1184 |
2,29227 |
0,177216 |
|
0,7 |
2,36827 |
23,7701 |
72,1693 |
1,49742 |
0,194912 |
|
0,8 |
2,32942 |
19,2125 |
77,5926 |
0,687136 |
0,178272 |
|
0,9 |
2,33538 |
16,1955 |
81,0601 |
0,195728 |
0,213248 |
|
1 |
1,74896 |
19,9887 |
78,0033 |
0,040256 |
0,218848 |
Численные эксперименты
Для сравнения динамики численностей рефлексирующих и нерефлексирующих особей были проведены численные эксперименты. Проводилось сканирование области параметров для следующих значений: a и c изменялись от 2 до 10 с шагом 0,16, b и d изменялись от 0,0001 до 0,0005 с шагом 0,000008, p изменялось от 0,1 до 1 с шагом 0,1. То есть для каждого параметра делалось 50 шагов в интервале его изменения. Для каждого набора параметров количество шагов по времени равнялось 1000 и начальные численности в каждой из стаций равнялись 1000 особей.
Для каждого значения цены перемещения p перебирались 504 наборов параметров a, b, c, d и вычислялись суммарные средние численности по обеим стациям за 1000 шагов по времени. Вычислялись следующие суммарные численности: N – средняя суммарная численность по двум стациям для модели без рефлексивного поведения особей; NR – средняя суммарная численность по двум стациям для модели с рефлексивным поведением; NRO – средняя суммарная численность по двум стациям при условии, что рефлексирующие и нерефлексирующие особи размножаются как отдельные подвиды. Для каждого набора параметров вычислялся максимум среди этих численностей. Для каждого значения p вычислялись: SN – количество максимальных значений для модели без рефлексии, SNR – количество максимальных значений для модели с рефлексией и SNRO – количество максимальных значений для модели с рефлексией и размножением как отдельные подвиды. Таким образом, мы выясняли, какая стратегия поведения особей дает им преимущество по численности для каждого набора параметров. В случае, когда для набора параметров все три средние суммарные численности были равны, вычислялось SRavn – количество совпавших средних суммарных численностей. В случае, когда совпали не все три, а две из средних численностей, вычислялось SS – количество таких случаев. В таблице показано процентное соотношение SN, SNR, SNRO, SRavn и SS к общему количеству наборов параметров (504 наборов) для каждого значения.
Как видно из таблицы, наиболее эффективным с точки зрения средней численности является рефлексивное поведение, когда рефлексирующие и нерефлексирующие особи размножаются как отдельные подвиды. Следующим по эффективности можно считать рефлексивное поведение особей, когда рефлексирующие и нерефлексирующие особи рассматриваются как один вид. Поведение при отсутствии рефлексии является наименее эффективным. Процент наборов параметров, при которых средние численности при различном поведении совпадают, монотонно убывает при росте параметра p.
Рецензенты:
Денисенко В.В., д.ф.-м.н., профессор, ведущий научный сотрудник, Институт вычислительного моделирования СО РАН, г. Красноярск;
Сомова Л.А., д.б.н., ведущий научный сотрудник, Институт биофизики СО РАН, г. Красноярск.