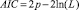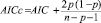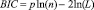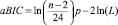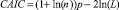Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Одним из условий применения IRT-моделей является необходимость соблюдения условия «одномерности» используемых эмпирических данных – ответы на задания конструкта должны зависеть только от одной латентной переменной (параметра). Но, несмотря на кажущуюся простоту, данное условие трудновыполнимо. Например, даже ответ на такой простой вопрос «сколько будет 2 + 2?» обусловлен не только умением складывать числа, но и рядом других латентных параметров: умением читать, знанием цифр и пр. Поэтому в настоящий момент считается, что если задание диагностирует исследуемый латентный параметр (главный), влияние других незначительно, задание удовлетворяет статистическим проверкам на соответствие [9], то его можно использовать для оценки латентного параметра. Однако некоторые теоретические исследования показывают, что игнорирование условия одномерности, а также локально-зависимых заданий [15] в ряде случаях приводит к необъективному оцениванию [14] либо к завышению надежности набора заданий (конструкта) [13].

В работе [2] рассматривается применение IRT-моделей для оценки компетенций студентов вузов. Базовая модель для оценки компетенций (латентная модель экзаменационных заданий, mRSM) формулируется в следующем виде 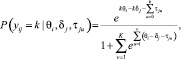[1]:

(1)

где y_ij – ответ, который дал i-й студент на j-е задание, 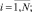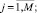N – количество студентов; M – количество заданий; θ_i – латентный параметр (компетентность) i-го студента; τ_ju – параметр (сложность категории) «шага» шкалы оценки по каждому экзаменационному заданию j; δ_j – параметр задания; k – оценка за задание; K – максимальная оценка.

Исходными данными являются оценки за ответы на выполненные экзаменационные задания. Экзаменационное задание по своей природе является собирательным, поэтому возникает вопрос об исследовании влияния множества компетенций на полученную экзаменационную оценку. Для этого можно использовать подход, рассмотренный в работах [6, 8], суть которого заключается в добавлении к исследуемой модели дополнительного параметра для учета влияния других латентных переменных – γ. Тогда модель (1) можно записать в следующем виде (TmRSM):

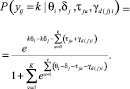(2)

Однако при использовании модели (2) возникают три существенные сложности:

1) увеличение числа параметров приводит к увеличению вычислительной сложности алгоритма;

2) использование большого числа параметров в некоторых случаях может не только не привести к повышению согласия эмпирических данных и модели, но и ухудшить его;

3) возрастает «сложность» задания исходных данных и интерпретации результатов. Поэтому задача определения «границ» использования одномерной модели является важной и зачастую определяющей для успешного применения модели в практической деятельности.

План исследования

Для анализа используются эмпирические данные об оценках студентов направления подготовки «Прикладная информатика», профиль подготовки «Информационные системы и технологии в управлении», квалификация (степень) бакалавр.

Статистический анализ применимости моделей проводится с использованием fit-статистик Infit, OutFit, InFit(t), OutFit(t) – считается, что следует использовать задания, у которых значения Infit и OutFit находятся в диапазоне 0,4–1,6, а InFit(t) и OutFit(t): –2,5...+2,5 [9].

Для сравнения моделей между собой использован ряд критериев, связанных с понятием информационной энтропии и расстоянием Кульбака – Лейблера [7]. При применении критериев лучшей считается модель, в достаточной мере полно описывающая данные с наименьшим количеством параметров. В работе использованы критерии Акаике, Байесовский и их модификации: состоятельный критерий Акаике, скорректированный критерий Акаике и скорректированный Байесовский критерий [4, 12] (табл. 1).

Также для сравнения можно использовать информационную функцию, введенную А. Бирнбаумом. По одному из определений, количество информации, обеспеченное j-м заданием в конкретной точке θ, – это величина, обратно пропорциональная стандартной ошибке измерения данного значения θ с помощью задания j [3]. Информационная функция задания показывает соответствие количества информации, получаемой при оценивании параметра θ с помощью задания j и может быть выражена следующей формулой:

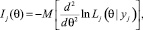(3)

где 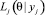– есть функция правдоподобия задания j.

Таблица 1

Информационные критерии

где p – количество оцениваемых параметров модели; L – максимизированное значение функции правдоподобия, n – размер выборки.

Значения этой функции являются своеобразной характеристикой эффективности j-го задания: чем больше количество информации, тем лучше, образно говоря, работает задание на рассматриваемом интервале оси θ. Информация, полученная при измерении данного θ с помощью всего конструкта, складывается из отдельных значений ординат информационных функций, построенных для каждого задания [5]:

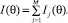(4)

Оценка параметров моделей, расчеты статистик и значений критериев производились с помощью программы, написанной на языке R [11].

Результаты исследования и их обсуждение

Рассмотрим компетенцию ПК-1. Определены 8 экзаменационных заданий, которые сформировали конструкт для оценки компетенции: правоведение, основы бизнеса, информационная безопасность, проектирование информационных систем, предметно-ориентированные экономические информационные системы, защита информации в банках, автоматизированные банковские системы, налогообложение. Дополнительно построена матрица (табл. 2), в которой цифрой 1 обозначены компетенции, влияющие на оценку соответствующего задания.

В табл. 3 приведены значения статистик параметров моделей, рассчитанные по экзаменационным оценкам.

Таблица 2

Матрица влияния компетенций на экзаменационные задания конструкта

Таблица 3

Значения fit-статистик

Анализируя таблицу, видно, что в целом обе модели достаточно хорошо описывают эмпирические данные, превышения значений статистик для некоторых параметров объясняются влиянием многомерности, к чему особенно чувствительна Outfit-статистика.

В табл. 4 приведены значения информационных критериев – мер относительно качества моделей, учитывающих степень «подгонки» модели под данные с корректировкой (штрафом) на используемое количество оцениваемых параметров.

Даже если исключить из рассмотрения AICc, который накладывает очень большой штраф на количество параметров, все равно увеличение количества параметров является очень существенным и сказывается на значениях всех прочих информационных критериев, согласно которым следует выбрать mRSM.

На рис. 1 в графическом виде представлены оценки компетенций студентов в логитах, рассчитанные по двум моделям.

Таблица 4

Значения информационных критериев

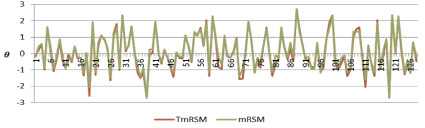
Рис. 1. График оценок компетенций студентов

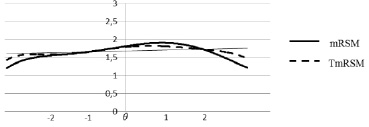
Рис. 2. Графики информационных функций конструкта

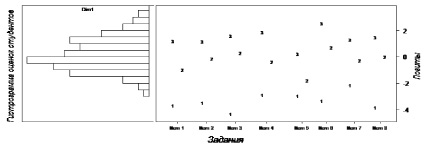
Рис. 3. Карта Райта

Абсолютная максимальная разница в оценках составила 0,6 логита, средняя разница – 0,13 логита, наибольшая разница проявляется на концах шкалы, при оценке θ в диапазоне (–1,5; +1,5) логита разница не превышает среднюю. Корреляция оценок – 0,99. В подавляющем большинстве случаев разница в оценке не превышает среднюю ошибку вычисления. На рис. 2 представлены графики информационных функций конструкта.

Для обеих моделей информационные функции имеют один выраженный максимум, что говорит о хорошем качестве конструкта. Сравнивая точности измерения компетенций, можно отметить, что у mRSM наибольшая точность достигается в диапазоне (примерно) θ ∈ (–0,5; +2), в диапазоне θ ∈ (–1,2; +0,5) точности равны, а по краям шкалы TmRSM показывает большую точность измерения. Однако данные различия не являются значительными, и в общем случае нельзя сделать однозначный вывод о том, какой модели следует отдать предпочтение. На рис. 3 представлена карта Райта для набора заданий оценки компетенции ПК-1. Оценки большинства студентов находятся в диапазоне (–2; +2) логита, где по точности mRSM не уступает TmRSM.

Результаты расчётов и анализа по остальным компетенциям ФГОС «Прикладная информатика» аналогичны приведённым для компетенции ПК-1.

Выводы

В статье с практической точки зрения рассмотрена проблема игнорирования условия одномерности при использовании одномерной IRT-модели оценки компетенции. Проведено сравнение одномерной модели mRSM с многомерной TmRSM, учитывающей влияние нескольких латентных переменных – компетенций. Проведенные расчеты показывают, что TmRSM в некоторых случаях более точно позволяет оценить компетенции, особенно у студентов с низким и/или высоким уровнем освоения компетенции, однако для студентов со средним уровнем освоения компетенции (а таких большинство) более предпочтительной является одномерная модель. Оценки компетенций студентов, полученные по mRSM и TmRSM, обладают очень высоким коэффициентом корреляции – минимальное значение 0,985 (по компетенции ПК-15), а абсолютная разница оценок в 96 % случаев не превышает ошибку измерения. Разумеется, нельзя не списывать со счетов и размер выборки – расчеты, проведенные на имитационных данных, например в работе [10], показывают, что с увеличением объема выборки расхождение в оценках параметров моделей растет. Но при небольшом и среднем размере выборки применение одномерной модели не приводит к существенному ухудшению точности оценки. В совокупности с усложнением процедуры оценки и алгоритмов расчетов TmRSM использование одномерной модели для практического применения следует считать допустимым.

Рецензенты:

Пархомов В.А., д.ф.-м.н., профессор кафедры информатики и кибернетики, ФГБОУ ВПО «Байкальский государственный университет экономики и права», г. Иркутск;

Боровский А.В., д.ф.-м.н., профессор кафедры информатики и кибернетики, ФГБОУ ВПО «Байкальский государственный университет экономики и права», г. Иркутск.