Системы прогнозирующего управления, именуемые в зарубежной литературе «Model Predictive Control (MPC)», зародились в начале 60-х годов 20-го века. Изначально свое применение данный подход нашел в нефтехимическом и энергетическом производстве, поскольку позволял решать задачи управления в случаях высокой сложности математических моделей объектов управления.
В настоящее время и сфера практического приложения MPC-методов, и их разнообразие существенно расширились.
Преимуществом MPC-подхода, которое позволило ему успешно развиться в практике построения и эксплуатации систем управления, является относительная простота базовой схемы формирования обратной связи, сочетающаяся с высокими адаптивными свойствами. Последнее обстоятельство позволяет управлять многомерными и многосвязными объектами со сложной структурой, включающей нелинейности, оптимизировать процессы в режиме реального времени в рамках ограничений на управляющие и управляемые переменные, учитывать неопределенности в задании объектов и возмущений [1].
Цель исследования
Задача исследования состоит в определении оптимального метода прогнозирующего управления электромагнитным приводом.
Материалы и методы исследования
В качестве материалов используется теоретическое описание принципов работы наиболее популярных методов прогнозирующего управления, их достоинства и недостатки. Используемые методы: анализ, структурирование и алгоритмизация.
Описание алгоритма прогнозирующего управления
Для описания работы алгоритма прогнозирующего управления предположим, что объект управления имеет структуру SISO (single-input, single-output), т.е. он представляет собой систему управления с одной переменной, одним входом и одним выходом. Также мы предполагаем, что время изменяется дискретно, и текущий момент времени обозначим k.
Основной принцип MPC заключается в определении в определенный момент времени k последовательности управляющих воздействий
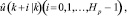
которая будет приложена к объекту, чтобы обеспечить максимальное совпадение траектории прогнозируемых значений выхода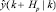 
с рекомендуемой траекторией движения r(k + i|k). Решается эта задача с помощью минимизации стоимостной функции [4]:
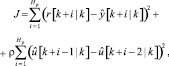
где ρ – коэффициент регуляризации входного сигнала.
Это общий вид функции стоимости прогнозирующего управления, в которой учитывается разница между рекомендуемой траекторией и спрогнозированной, а также уровень сигнала управления. Функция может меняться от метода к методу.
Для более подробного описания рассмотрим рис. 1 [11], на котором представлены сигналы, участвующие в алгоритме работы прогнозирующего управления. На данном рисунке представлены следующие виды сигналов:
● s(t) – установленная траектория, по которой должен следовать выход в идеале;
● r(t|k) – рекомендуемая траектория, вдоль которой значение выхода объекта должно вернуться к s(t), начинается с y(k);
● 
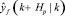– свободный отклик, который будет получен если будущая входная траектория останется в последнем состоянии u(k – 1);
● 
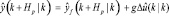– спрогнозированный выход в момент времени k + Hp, где 
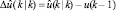– разница между текущим значением u(k – 1) входа и спрогнозированным 
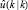, g – отклик модели на дискретный входной шаг горизонта прогноза Hp.
Перед описанием самого алгоритма работы следует отметить несколько моментов. Предсказанное поведение зависит от прогнозируемой входной траектории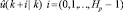 
. Значение спрогнозируемой входной последовательности 
лучше значений реального входного сигнала u определяет в момент k, какой вход в момент k + i должен быть; реальный входной сигнал u(k + i) будет, вероятнее всего, отличаться от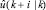 
.
В регуляторе имеется внутренняя модель, которая используется для прогноза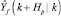 
свободного отклика объекта, начинающегося в текущий момент времени k и вдоль будущего горизонта предсказания k + Hp.
Далее рассмотрим обобщенный алгоритм работы прогнозирующего управления:
1. В момент времени k регулятор получает выходное измерение y(k).
2. На основе y(k) определяется новая рекомендуемая траектория r(k + i|k).
3. Делается прогноз свободного отклика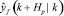 
вдоль горизонта k + i, где i = 1, 2, …, Hp.
4. Делается предположение, что спрогнозированный отклик объекта соответствует рекомендуемой траектории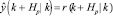 
. Из этого предположения определяется входное воздействие 
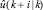, где i = 0, 1, …, Hp – 1. Входное воздействие определяется по формуле
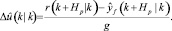
5. Новое значение входа применяется к объекту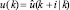 
, момент времени смещается k = k + 1.
Согласно концепции удаляющегося горизонта, в момент времени k только первое значение входа (Δu(t)) вектора будущих приращений сигнала управления или последовательности (u) реально применяется к объекту. Оставшиеся оптимальные входы отбрасываются, и новая задача оптимального управления решается в момент времени t + 1 [11].
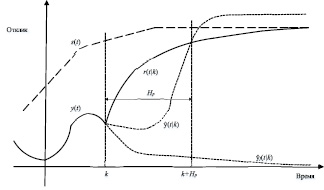
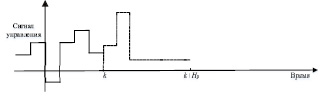
Рис. 1. Принцип работы алгоритма прогнозирующего управления
Варианты реализации прогнозирующего управления
Рассмотрим более подробно наиболее распространенные методы прогнозирующего управления [10]:
● Динамическое матричное управление – Dynamic matrix control (DMC).
● Модельное алгоритмическое управление – Model algorithmic control (MAC).
● Прогнозирующее функциональное управление – Predictive functional control (PFC).
● Расширенное прогнозирующее – самоадаптивное управление Extended prediction self-adaptive control (EPSAC).
● Расширенное интервальное адаптивное управление – Extended horizon adaptive control (EHAC).
● Обобщенное прогнозирующее управление – Generalized predictive control (GPC).
● Нейросетевое инверсное прогнозирующее управление.
Динамическое матричное управление (DMC)
В DMC динамическая матрица используется для прогнозирования будущих значений, метод основан на модели пошагового отклика процесса. Алгоритм используется для линейных открытых стационарных процессов (linear open loop stable process) [6].
Суть DMC регулятора заключается в управлении выходным сигналом объекта управления по методу наименьших квадратов со штрафным членом в сигнале управления. Блок-схема работа алгоритма представлена на рис. 2 [4].
Для случая SISO (один вход – один выход) модель отклика объекта:
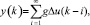
где g – коэффициент отклика объекта на входное возмущение Δu(k – i); k – момент времени.
Предсказанное значение выхода объекта с возбуждением:
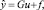
где G – динамическая матрица коэффициентов отклика модели на дискретный входной шаг горизонта прогноза, f – свободный отклик объекта.
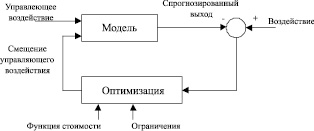
Рис. 2. Блок-схема алгоритма управления DMC
.
Функция стоимости, которая должна быть минимизирована согласно алгоритму, включая изменение сигнала управления, выглядит следующим образом:
,
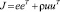где ρ – коэффициенты регуляризации входного сигнала; u – вектор наращивания сигнала управления; e – вектор будущих ошибок, равен уровню спрогнозированного возмущения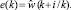 
Решение этой функции стоимости может быть получено вычислением производной от J и приравниванием ее к нулю.
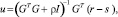
где r – рекомендуемая траектория; s – свободный отклик объекта.
Стандартное квадратичное программирование в каждый момент выборки осуществляет оптимизацию.
Для DMC алгоритма для реализации закрытой схемы требуется большая длина горизонта прогноза [13].
ДМУ особенно успешен в нефтехимической индустрии с многофакторными процессами.
Модельное алгоритмическое управление (MAC)
MAC использует импульсную модель отклика. Этот метод очень похож на DMC со следующими различиями:
● Вместо модели шагового отклика с участием Δu применяется импульсная модель отклика с участием u.
● Количество изменений входа не настраивается.
● Оценка возмущения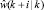 
фильтруется.
Управление многофакторным процессом представлено его импульсными откликами (содержатся во внутренней модели), используемыми на линии прогноза [12].
Управление многофакторным процессом представлено его импульсными откликами (содержатся во внутренней модели), используемыми на линии прогноза [4].
Рассмотрим линейную систему с усеченным импульсным откликом:
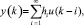
где hi – коэффициенты импульсного отклика, u – вектор сигнала управления.
С учетом возмущений прогноз может быть записан как
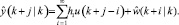
Прогноз без возмущений:
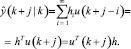
Сначала через горизонт прогноза N вычисляется модель рекомендуемой траектории r(k) первого порядка:
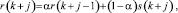
j = 1, 2, …, N,
где α – коэффициенты прогнозирующей модели; r – идеальная траектория.
Затем вычисляется прогноз вдоль горизонта.
Если входная переменная изменяется вдоль горизонта прогноза:
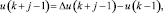
j = 1, 2, …, N.
Предсказатель может быть записан как
y = Hu + yf.
Закон управления MAC (без ограничений):
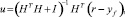
где
Этот закон проще относительно других формулировок.
Горизонт прогноза, коэффициент штрафования и α – это все настраиваемые параметры. α выбран как главный настраиваемый параметр.
В MAC импульсный отклик позволяет усилить робастность против ошибок идентификации.
MAC применим только для стабильных процессов с открытой схемой. MAC используется в энергетике, стекловыпекании, парогенераторах и др.
Прогнозирующее функциональное управление (PFC)
В PFC ценится его гибкость и эффективность. PFC алгоритм требует метода оптимизации в реальном времени.
Точки совпадения и базисная функция – две характеристики PFC. Точка совпадения используется для упрощения вычислений, учитывая только набор точек в горизонте прогноза. Желаемые и прогнозируемые значения выхода объекта должны совпадать только в определенном наборе точек вдоль горизонта прогноза, а не на всем горизонте.
Выбор базисной функции зависит от характеристики процесса и желаемой идеальной траектории. Она определяет входной профиль вдоль горизонта прогноза, используя малый набор параметров.
Согласно модели пространства состояний, которая наиболее часто применяется в PFC [4]
w(t) = Aw(t – 1) + Bu(t – 1);
y(t) = Cw(t).
Прогноз осуществляется путем добавления члена автоматической компенсации,
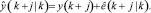
Будущий сигнал управления устроен как линейная комбинация базисных функций,
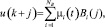
где μi – коэффициенты линейной комбинации базисных функций; Bi – базисная функция.
Функция стоимости выглядит следующим образом:
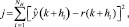
где hi = общее количество точек совпадений; r(k + j) = s(k + j) – αj(s(k) – y(k)); s – идеальная траектория.
PFC использует постоянную времени рекомендуемой траектории как главный настраиваемый параметр. Меньшее значение временной константы приводит к более агрессивному управлению, пока большее значение временной константы приводит к более агрессивным действиям.
Этот алгоритм робастен к ошибкам моделирования. Простота настройки и обслуживания являются преимуществами PFC.
Фиксированная модель PFC не может гарантировать хорошее качество, когда применяется к сложным объектам, изменяющимся во времени.
PFC используется в таких процессах, как управление роботами, ракетами, реакторами, нагревателями и т.д. Он также используется в черной металлургии и алюминиевой промышленности.
Расширенное прогнозирующее самоадаптивное управление – (EPSAC)
EPSAC использует дискретную (z-преобразование) функцию передачи для моделирования процесса [7, 8].
Для прогнозирования процесс моделируется с возмущениями:
A(z–1)y(k) = B(z–1)u(k – d) + w(k);
w(k) = C(z–1)e(k).
Вектор параметров оценивается с помощью рекурсивного (расширенного) метода наименьших квадратов:
∆y(k) = ϕT(k)∙θ(k) + η(k),
где ϕT – вектор измерений; θ(k) – вектор параметров.
Прогноз на J шаг вперед (J = 2, 3, ..., N) выход процесса (без возмущений) осуществляется с помощью многоступенчатого предсказателя:
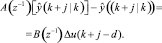
Учитывая
∆u(k + j) = 0, j > 0,
значение сигнала управления получают минимизируя функцию стоимости:
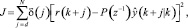
где P(z–1) – спроектированный полином с единым статическим коэффициентом усиления
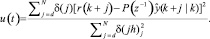
Это показывает, что структура закона управления очень проста и вычисление сводится к одному значению u(t).
Возможные параметры настройки – это горизонт предсказания, весовой коэффициент и фильтр-полином. Однако настройка в реальном времени горизонта прогноза влияет на структуру многоступенчатого предсказателя и структуру управления.
Расширенное интервальное адаптивное управление – (EHAC)
Основная идея EHAC заключается в вычислении последовательности входов в каждый момент выборки [u(k), u(k + 1), …, u(k + N – d)], чтобы свести к минимуму несоответствие между моделью и рекомендуемой траекторией в момент (k + N):
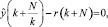N ≥ d.
Другая стратегия заключается в предположении, что управляющий сигнал постоянен u(k) = u(k + 1) = … = u(k + N – d) в интервале [k, k + N – d]. Стоимостная функция тогда
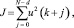N ≥ d.
Функция стоимости с учетом возмущений [4]:
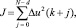
где ∆u(k + j) = u(k + j) – u(k + j – 1).
Первый элемент сигнала управления, который минимизирует индекс стоимостной функции:
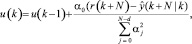
где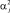 
– это коэффициент ∆u(k – j) в уравнении прогноза.
Таким образом, закон управления зависит только от параметров процесса, и настраиваемый параметр в методе EHAC это только горизонт прогноза N.
Алгоритм не требует знания систем матричного исчисления и терпим к эффекту выходных возмущений [9]. Однако многопараметрические регуляторы, основанные на одношаговом критерии прогноза, чувствительны к выбору структуры задержки. Циклическое поведение избегается использованием отступающего горизонта прогноза [14].
Обобщенное прогнозирующее управление (GPC)
Обобщенное прогнозирующее управление (GPC) – один из наиболее популярных прогнозирующих алгоритмов управления. Основное различие между GPC и DMC заключается в модели используемой для описания объекта и формирования динамической матрицы. Эта модель является более подходящей в промышленных приложениях, где возмущения не являются стационарными.
GPC используется для получения хорошего предсказания выхода и оптимизации последовательности будущих управляющих сигналов с целью минимизации многоступенчатой функции стоимости, определенной вдоль горизонта прогнозирования. Включение возмущения необходимо для отображения правильной структуры регулятора.
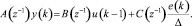
Спрогнозированный выход зависит от предыдущих значений выхода и предыдущих и будущих значений сигнала управления.
Для генерации набора спрогнозированных выходов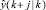 
используется уравнение спрогнозированной модели
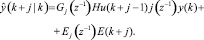
Значение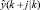 
для j > k зависит от будущих значений сигнала управления u(k + j). Эти управляющие сигналы используются для достижения цели в GPC с помощью минимизации функции стоимости, данной как
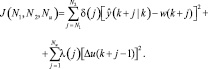
Предполагая, в открытом цикле, сигнал управления вычисляется, игнорируя будущую последовательность шума. Тогда оптимальное значение прогноза может быть
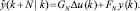
Ожидаемая выходная последовательность равна первой колонке матрицы G. Если время задержки объекта d > 1, то первые d – 1 строки G будут нулями. Когда N1 = d, тогда ведущий элемент ненулевой. Ожидаемая функция стоимости может быть записана как
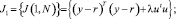
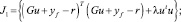
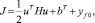
где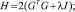 
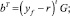
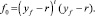
В случае отсутствия ограничений будущий сигнал управления для минимизации стоимости
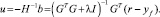
Первый элемент управляющего сигнала u:
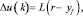
где L – это первая строка матрицы
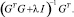
Текущий управляющий сигнал
.
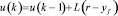Для r –yf = 0 нет изменения сигнала управления.
GPC применим к системам неминимально-фазовым, с разомкнутым контуром нестабильным и имеющим изменяющееся время задержки. Он способен учитывать как постоянные, так и изменяющиеся будущие значения контрольных точек.
GPC показывает более высокую производительность в цементных мельницах, башнях для сушки распыления и роботизированных руках [5].
Нейросетевое инверсное прогнозирующее управление
В последнее время стало активно развиваться направление интеллектуализации существующих подходов управления и создание принципиально новых стратегий на базе искусственного интеллекта. Одним из таких новых подходов является нейросетевое инверсное прогнозирующее управление. Широкое распространение такого способа управления связано с тем, что применение нейронных сетей позволяет повысить качество переходного процесса, по сравнению с другими методами.
Блок-схема нейросетевого инверсного прогнозирующего управления представлена на рис. 3 [2].
Суть нейросетевого прогнозирования заключается в использовании в качестве регулятора нейронной сети, обученной переводить объект из текущего состояния в желаемое за указанный горизонт прогноза g.
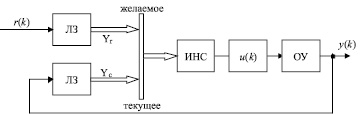
Рис. 3. Блок-схема нейросетевого инверсного прогнозирующего управления
При этом измеренная и заданная траектория выходного сигнала объекта принимают вид
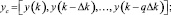
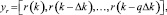
где r(t) – сигнал задания системы управления (рекомендуемая траектория); Δk – период дискретизации; q – число задержанных значений в образуемых векторах.
Основной настраиваемый параметр, используемый в нейросетевом прогнозирующем управлении, – это горизонт прогноза. Например, уменьшение горизонта прогноза приводит к повышению точности модели, а также к увеличению быстродействия системы, что сопровождается увеличением амплитуды управления.
Для работы данной схемы управления предварительно нужно обучить нейронную сеть. Один из возможных вариантов обучения нейронной сети для задач управления представлен на рис. 4.
Рис. 4. Блок-схема обучения нейросетевого инверсного прогнозирующего регулятора
Рис. 5. Блок-схема работы нейросетевого инверсного прогнозирующего регулятора с электромагнитным механизмом (ЭМ) в качестве объекта управления
Схема работает следующим образом, на вход объекта управления подается случайный тестовый сигнал u(t) и регистрируется возникающий при этом фактический выход объекта y(t), на основе которого с помощью задержек формируются регрессионные векторы:
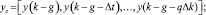
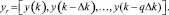
Возникающая пара состояний, с опережением одним другого на время горизонта прогноза, моделирует ситуацию желаемого перехода объекта из текущего состояния в желаемое под воздействием сигналов управления.
Объект управления и выбор схемы управления
Объектом прогнозирующего управления выступает электромагнитный привод, который включает как исполнительный элемент, так и систему управления. При проведении экспериментальных разработок новой продукции важными вопросами являются настройка параметров регуляторов. К устройствам данного класса, в частности используемых в составе систем повышенной ответственности, предъявляются требования по обеспечению высокой надежности работы. Сложность и непрерывное совершенствование применяемых в настоящее время магнитных систем требует новых высокоточных подходов к управлению положением их подвижных элементов.
Положение подвижного элемента электромагнита x определяет степень замкнутости магнитной цепи d. Степень замкнутости магнитной цепи d определяет уровень магнитного потока Ф при заданном значении магнитодвижущей силы Iw [3]. Уровень магнитного потока имеет прямую взаимосвязь с потокосцеплением обмотки магнитопровода ψ. Таким образом, существует физическая взаимосвязь между вебер-амперной характеристикой электромагнита ψ(Iw) и положением его подвижного элемента x:
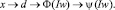
В условиях сложности конструкции и неопределенности отдельных параметров новых экспериментальных образцов продукции, традиционные методы разработки систем управления не являются эффективными. С учетом рассмотренных ранее методов прогнозирующего управления для решения данной задачи предлагается использовать регуляторы на базе нейронных сетей, т.е. применить стратегию инверсного прогнозирующего нейроуправления. Данный выбор обосновывается определенными свойствами нейронных сетей, которые обеспечиваются их внутренней структурой и устройством.
1. Отказоустойчивость при аппаратной реализации нейронной сети. Нейронные сети потенциально отказоустойчивы: при неблагоприятных условиях их производительность падает незначительно.
2. Потенциальное сверхвысокое быстродействие. Нейронные сети обладают потенциальным сверхвысоким быстродействием за счет использования массового параллелизма обработки информации.
3. Устойчивость к шумам во входных данных. Возможность работы при наличии большого числа неинформативных, шумовых входных сигналов. Нет необходимости делать их предварительный отсев, нейронная сеть сама определит их малопригодность для решения задачи и отбросит их.
4. Адаптирование к изменениям окружающей среды. Нейронные сети обладают способностью адаптироваться к изменениям окружающей среды. В частности, нейронные сети, обученные действовать в определенной среде, могут быть легко переучены для работы в условиях незначительных колебаний параметров среды. Более того, для работы в нестационарной среде (где статистика изменяется с течением времени) могут быть созданы нейронные сети, переучивающиеся в реальном времени.
Исходя из описания объекта управления и выбранной структуры регулятора, предлагается следующая схема управления электромагнитным приводом (рис. 5).
При этом управляющими сигналами выступает значение тока, подаваемого на ЭМ в момент времени k – I(k). Выходным сигналом с объекта управления будет выступать функция положения якоря x(k). На блок-схеме рис. 5 xr(k) – желаемое значение выхода ЭМ.
Заключение
В результате анализа и обзора методов прогнозирующего управления инверсный нейросетевой прогнозирующий регулятор выбран как наиболее подходящий для управления электромагнитным приводом. Предложена блок-схема управления электромагнитом.
Результаты работы получены при поддержке гранта РФФИ № 15-38-20652 «Развитие теории бессенсорных прогнозирующих методов управления и диагностики электроприводов».
Рецензенты:
Горбатенко Н.И., д.т.н., зав. кафедрой «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск;
Кириевский Е.В., д.т.н., профессор кафедры «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск.