Задача об определении давления в вертикальном потоке газа в скважине в общем случае приводит к необходимости решения нелинейных уравнений и поэтому не исследована окончательно даже для простейшего случая однородного потока газа [2, 3].
Вместе с тем ее решение необходимо для проведения расчетов зависимости плотности, скорости, давления и температуры в газовой скважине [4]. Такие задачи неизбежно возникают при определении технологического режима работы газовых скважин.
Использованное здесь стационарное уравнение движения включает силу трения Fтр.
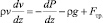(1)
В общем случае плотность определяется из уравнения состояния и является функцией температуры и давления ρ = ρ(P, T). Учет зависимости плотности от температуры сильно усложняет задачу. Однако в ряде задач зависимостью плотности от температуры можно пренебречь.
В баротропном приближении плотность газа является функцией давления ρ = ρ(P) или обратно – давления от плотности P = P(ρ). Очевидно, что для изотермических процессов справедливо баротропное приближение. Оно применимо также при относительно небольших перепадах температуры. Применительно к реальным скважинным условиям это оправдано, поскольку перепады давления составляют десятки атмосфер, т.е. порядка 1000 % по отношению к атмосферному. В то же время перепады температуры порядка 10 °С составляют около 3 % по отношению к нормальному значению. Впрочем, баротропное приближение строго справедливо не только для изотермических, но и, например, для адиабатических и других политропных процессов в идеальном газе.
В случае ламинарного потока газа сила внутреннего трения определяется через массовый дебит скважины Q
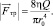(2)
Поскольку средняя по сечению скважины скорость потока и дебит скважины связаны соотношением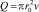 
, то сила трения пропорциональна средней по сечению скорости газа [5]:
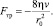(3)
В вертикальном восходящем потоке газа происходит увеличение скорости за счет уменьшения плотности. При этом ламинарный режим течения неизбежно переходит в турбулентный. При течении газа с плотностью r = 71,4 кг/м3, вязкостью η = 10,27∙10–6 Па·с при нормальных условиях и значении критического числа Рейнольдса Reкр = 2300 в трубе диаметра d = 0,062 м скорость, при которой ламинарное течение сменяется турбулентным, составляет v = 0,01 м/c. Поскольку указанная смена режимов течения может происходить в некотором диапазоне скоростей, то для верхней границы критического числа Рейнольдса Re = 5,9∙105 при тех же условиях течения скорость будет равна v = 1,37 м/c. Такой диапазон скоростей соответствует дебитам от 0,2 до 40 т/сут.
В турбулентном потоке средняя скорость зависит от градиента давления более сложным образом [1]:
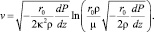(4)
В подкоренном выражении введен знак минус, поскольку градиент давления отрицательный при движении газа в положительном направлении оси z.
Поскольку зависимость (4) не позволяет явно выразить зависимость градиента давления от скорости течения, то представим ее в обобщенной форме
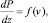(5)
где функция f является такой, что обратная к ней совпадает с (4).
Общие закономерности зависимости средней скорости ламинарного и турбулентного потоков от градиента давления и градиента давления от средней скорости потока иллюстрируются на рис. 1–4. Для расчета кривых использованы следующие значения параметров скважины: D = 2000 м, r0 = 0,031 м; наполняющего флюида – метан: M = 16,04∙10–3 кг/моль, r = 71,4 кг/м3, η = 10,26∙10–6 Па∙с; g = 9,8 м/с2, R = 8,31 Дж/(моль∙К), T = 300 К.
Рис. 1 иллюстрирует зависимость средней скорости ламинарного и турбулентного потока газа от градиента давления. Из сопоставления кривых, приведенных на рис 1, следует, что при турбулентном режиме величина средней скорости при градиенте давления около 10 Па/м на два порядка ниже, чем при ламинарном.
Рис. 2 иллюстрирует зависимость средней скорости потока газа от градиента давления с учетом изменения режима течения с ламинарного на турбулентный при некотором критическом значении градиента 0,01 Па/м. Из рисунка следует, что при указанных значениях параметров в ламинарном режиме наблюдается линейное возрастание средней по сечению скорости, которое при достижении критического градиента скачкообразно уменьшается в несколько раз.
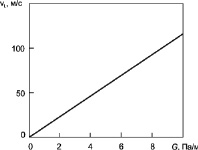
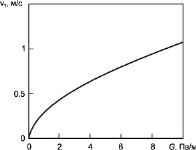
а б
Рис. 1. Зависимость средней скорости ламинарного (а) и турбулентного (б) потока газа в трубе от градиента давления
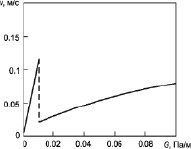
Рис. 2. Зависимость средней скорости потока газа от градиента давления с учетом смены режимов течения
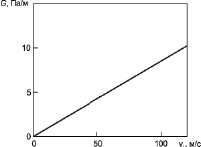
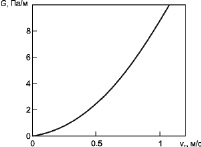
На рис. 3 представлена зависимость градиента давления от средней скорости ламинарного и турбулентного потока газа. Рисунок позволяет судить о величине градиента давления в зависимости от режима течения.
Зависимость градиента давления от средней скорости потока газа с учетом смены режима течения показана на рис. 4. Из кривой, приведенной на рисунке, следует, что изменение режима течения сопровождается скачкообразным возрастанием градиента давления. Проиллюстрированная на рисунке закономерность положена в основу исследования поля давления газового потока в скважине с учетом смены режима течения.
а б
Рис. 3. Зависимость градиента давления от средней скорости ламинарного (а) и турбулентного (б) потока газа
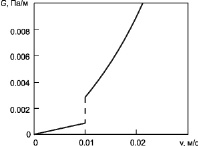
Рис. 4. Изменение градиента давления в зависимости от средней скорости потока газа с учетом перехода течения из ламинарного в турбулентное
Уравнение движения, учитывающее смену режимов течения, с учетом (3) представится как
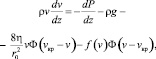(6)
где Ф(x) – единичная функция Хевисайда.
В случае, когда пространственное ускорение потока равно нулю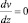 
, в отсутствие гравитационных сил из (6) следует формула
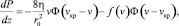(7)
из которой при v < vкр следует известная формула Пуазейля,
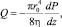(8)
а при v > vкр – аналогичная зависимость дебита от градиента давления для турбулентного потока
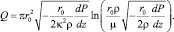(9)
Такое согласие дополнительно свидетельствует о достоверности принятой концепции.
Из уравнения неразрывности для стационарного случая имеем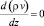 
. Отсюда следует ρv = ρ0v0, что позволяет определить зависимость скорости от плотности
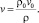(10)
С учетом зависимости (6) уравнение движения приводится к виду
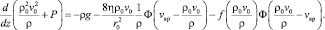(11)
Далее воспользуемся известной формулой для производной сложной функции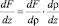 
, тогда получим дифференциальное уравнение для определения поля давления в скважине:
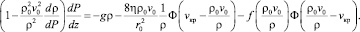(12)
Разделяя переменные в этом уравнении, получим неявную зависимость поля давления от пространственной координаты и определяющих процесс физических параметров:
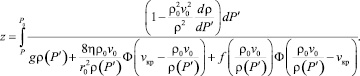(13)
В частном случае для адиабатического процесса в идеальном газе получим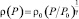 
Подстановка полученного выражения в уравнение (13) приводит к следующему соотношению:
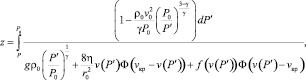(14)
где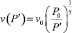 
. В случае ламинарного течения зависимость (15) приобретает вид
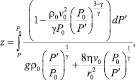(15)
а в турбулентном потоке
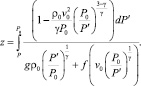(16)
Формула (14) позволяет построить зависимости давления от вертикальной координаты для стационарного дозвукового потока газа. На рис. 5 представлены результаты расчетов давления газа в стволе скважины при дебите 100 т/сут для различных режимов течения газа. Для расчета кривых использованы указанные выше значения параметров скважины и наполняющего флюида.
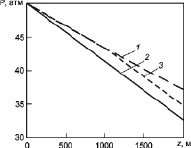
Рис. 5. Зависимости давления газа в скважине от глубины при различных режимах течения: 1 – ламинарный поток; 2 – турбулентный поток; 3 – поток с изменяющимся режимом течения
Кривая 2, выделенная на рисунке сплошной линией, соответствует турбулентному режиму течения и наиболее часто реализуется на практике, поскольку критические значения скорости малы. Кривая 1 построена для случая, если бы ламинарное течение сохранялось во всем диапазоне скоростей.
Кривая 3 описывает поле давлений для случая, когда на глубине 1000 м происходит смена режима течения с ламинарного на турбулентный. Поэтому в диапазоне глубин до 1000 м кривая 3 совпадает с кривой 1 для ламинарного течения. В диапазоне глубин от 1000 до 2000 м кривая 3 соответствует турбулентному режиму течения и симулирует кривую 2, описывающую турбулентный режим течения.
Итак, развитая математическая модель позволяет исследовать поля давления газа в стволе действующей скважины с учетом смены режима течения в диапазоне дозвуковых скоростей и может быть использована для практических расчетов.
Обозначения
Латинские: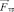 
– сила внутреннего трения, Н; 
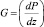– градиент давления, Па/м; 
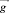– вектор ускорения свободного падения, м/с2; M – молярная масса газа, кг/моль; P – поле давления внутри скважины, Па; Q – массовый дебит скважины, т/сут; r0 – внутренний радиус трубы, м; R – универсальная газовая постоянная, равная 8,31 Дж/(моль·К); T – температура газа, К; 
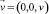– поле скоростей газа в трубе, м/c; v0 – фиксированное значение средней скорости по сечению трубы, м/c; vкр – критическое значение скорости, м/c; z – вертикальная координата; м.
Греческие: π – число Пи, равное 3,14; κ – постоянная Кармана, равная 0,4; η – динамическая вязкость газа, Па·с; μ – кинематическая вязкость газа, Па·с; ρ, ρ0 –плотность газа и ее фиксированное значение соответственно, кг/м3.
Рецензенты:
Галиев А.Л., д.т.н., профессор, директор филиала ФГБОУ ВПО «Уфимский государственный авиационный технический университет», г. Стерлитамак;
Сабитов К.Б., д.ф.-м.н., профессор, директор ГАНУ «Институт прикладных исследований Республики Башкортостан», г. Стерлитамак.