В условиях обработки металлов давлением среди таких факторов, влияющих на пластичность, как состав и структура деформируемого металла, характер напряженного состояния при деформации, скорость деформации и др., – является температура деформации.
Вопросами моделирования температурных полей, описывающими температурные процессы, происходящие в очаге деформации и технологическом потоке стана, занимались многие ученые. Для создания данного алгоритма была использована модель [1], где для практических расчетов температуры в многоклетевых станах используется упрощенная модель, которая имеет вид
Ui = Ui–1 – ∆Uu – ∆Uk – ∆Ub + ∆Ud, (1)
где Ui – температура на выходе из i-й клети; Ui–1 – температура на выходе из предыдущей клети или температура начального нагрева заготовки в нагревательном устройстве; ∆Uu – теплопередача излучением в окружающую среду; ∆Uk – конвективная теплопередача; ∆Ub – контактный теплообмен с рабочими валками; ∆Ud – разогрев металла за счет энергии пластической деформации.
В работе [2] эта модель реализована с помощью метода конечных элементов.
При численном решении задач распределения температурного поля по клетям закрытого прокатного стана для линии непрерывного литья и прокатки металлической катанки одним из наиболее употребительным методом является метод сеток.
Простота и универсальность характерны для разностных методов решения краевых задач математической физики в регулярных расчетных областях, а использование нерегулярных сеток сближает метод конечных разностей с методом конечных элементов.
В работе был использован экономичный разностный метод для решения многомерных уравнений в частных производных [3], метод суммарной аппроксимации, который позволяет получить абсолютно устойчивые сходящиеся локально-одномерные схемы для уравнений параболического типа.
Цель исследования
Рассмотрим задачу для уравнения теплопроводности в виде [2]:
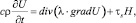 (2)
(2)
где c – удельная теплоемкость металла; ρ – массовая плотность металла; λ – коэффициент теплопроводности; τs – сопротивление металла пластической деформации сдвига; H – интенсивность скоростей деформации сдвига, со следующими граничными условиями:
1. На входе в очаг деформации температура металла известна.
2. На свободной поверхности имеет место теплопередача излучением в окружающую среду, которая описывается формулой Стефана ‒ Больцмана.
3. На контактной поверхности имеет место теплообмен между деформируемым металлом и поверхностью валков, описываемый выражением
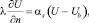 (3)
(3)
где αs – коэффициент теплопередачи на контактной поверхности; Ub – температура валков.
4. На остальных поверхностях, ограничивающих 1/4 часть очага деформации, тепловой поток равен нулю.
По теории в большинстве процессов обработки металла давлением форма заготовки отличается от формы готового изделия, определяемой формой инструмента. Чем ближе элемент находится к углу сечения, тем меньшее удлинение он получит. Поэтому стороны сечения получат выпуклую форму. Квадратное сечение будет приближаться к круговому, а прямоугольное – сначала к эллипсу, а затем все равно к кругу. Так как черновые калибры предназначены для постепенного формирования прокатываемого профиля, а также к черновым относят калибры простой формы (прямоугольный, ромб, овал, круг, квадрат), для эксперимента при выборе формы калибров клетей было взято прямоугольное сечение.
Разностное уравнение
Рассмотрим трехмерное параболическое уравнение второго порядка [3]:
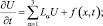 (4)
(4)
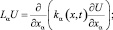 (5)
(5)
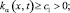 c1 = const, (6)
c1 = const, (6)
где x = (x1, x2, x3) – точка 3-мерного пространства с координатами x1, x2, x3. Пусть G – произвольная 3-мерная область с границей Г, 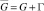 ,
,
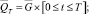
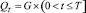 .
.
Требуется найти непрерывное в цилиндре 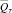 решение уравнения (6), удовлетворяющее краевому условию
решение уравнения (6), удовлетворяющее краевому условию
U = μ(x, t) при x ∈ Γ, 0 ≤ t ≤ T (7)
и начальному условию
U(x, 0) = U0(x), при 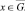 (8)
(8)
Как обычно, предполагается, что эта задача имеет единственное решение U = U(x, t), обладающее всеми требуемыми по ходу изложения производными.
При построении локально-одномерной схемы формально заменим трехмерное уравнение цепочкой одномерных уравнений, т.е. аппроксимируем с шагом  последовательно операторы
последовательно операторы
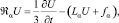 α = 1, 2, 3, (9)
α = 1, 2, 3, (9)
где fa удовлетворяет условию 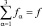 .
.
Для аппроксимации LaU + fa на пространственной сетке ωh воспользуемся однородным разностным оператором второго порядка аппроксимации Λαy + φα. Граничные условия и правая часть φα берутся в произвольные моменты времени:
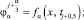
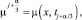 α = 1, 2, 3.
α = 1, 2, 3.
Аппроксимируя каждое уравнение теплопроводности номера α на интервале 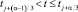 двухслойной схемой с весами, получим цепочку p одномерных схем, которая называется ЛОС:
двухслойной схемой с весами, получим цепочку p одномерных схем, которая называется ЛОС:
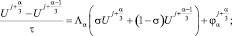 α = 1, 2, 3, x ∈ ωh, (10)
α = 1, 2, 3, x ∈ ωh, (10)
где σ – произвольное число. При σ = 1 получим чисто неявную локально-одномерную схему, а при σ = 0 ‒ явную ЛОС.
Рассмотрим чисто неявную ЛОС:
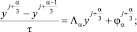 α = 1, 2, 3, x ∈ ωh. (11)
α = 1, 2, 3, x ∈ ωh. (11)
Краевое условие:
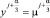 при x ∈ γh,α, j = 0, 1, ..., j0; α = 1, 2, 3. (12)
при x ∈ γh,α, j = 0, 1, ..., j0; α = 1, 2, 3. (12)
Начальное условие:
y(x, 0) = u0(x). (13)
Остановимся более подробно на (11):
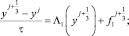
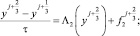
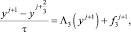
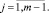 (14)
(14)
Краевые условия:
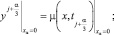
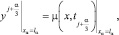 α = 1, 2, 3. (15)
α = 1, 2, 3. (15)
Начальное условие:
y0 = U0(x). (16)
Рассмотрим каждое из трех уравнений (14) отдельно. Первое из уравнений (14) записываем в виде
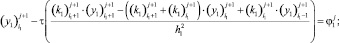
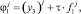 (17)
(17)
где 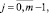
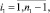
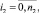
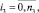
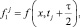
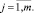
Выражение (17) перепишем в виде
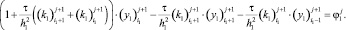 (18)
(18)
Обозначая через
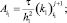
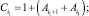
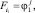
получим
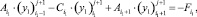
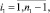
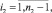
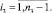 (19)
(19)
Граничные условия в общем виде:
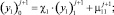
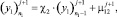 (20)
(20)
здесь χ1 = 0, χ2 = 0 – граничные условия 1-го рода, 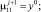
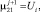 где Ui – температура на выходе из i-й клети в (1).
где Ui – температура на выходе из i-й клети в (1).
Далее подставляя известные значения y0, вычисляем F1, затем методом прогонки решаем задачу (19) во всех узлах сетки ωh:
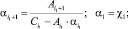
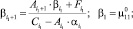
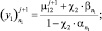
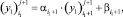
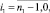
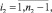
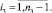 (21)
(21)
Второе из уравнений (14) записываем в виде
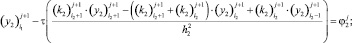
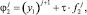 (22)
(22)
где 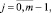
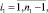
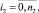
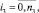
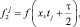
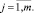
Выражение (22) перепишем в виде
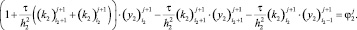 (23)
(23)
Обозначая через
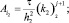
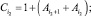
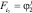
получим
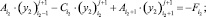
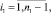
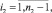
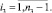 (24)
(24)
Граничные условия в общем виде:
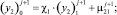
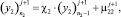 (25)
(25)
где 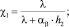
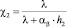 – граничные условия 3-го рода.
– граничные условия 3-го рода.
Далее подставляя известные значения 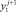 , вычисляем F2, затем методом прогонки решаем задачу (24) во всех узлах сетки ωh:
, вычисляем F2, затем методом прогонки решаем задачу (24) во всех узлах сетки ωh:
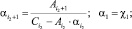
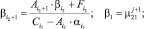
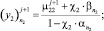
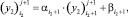
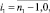
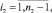
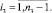 (26)
(26)
Третье из уравнений (14) записываем в виде
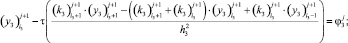
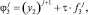 (27)
(27)
где 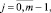
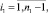
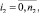
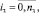
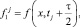
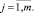
Выражение (27) перепишем в виде
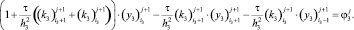 (28)
(28)
Обозначая через
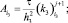
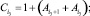
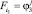
получим
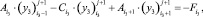
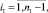
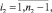
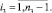 (29)
(29)
Граничные условия в общем виде:
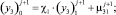
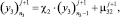 (30)
(30)
где 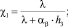
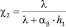 – граничные условия 3-го рода.
– граничные условия 3-го рода.
Далее подставляя известные значения 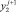 вычисляем F3, затем методом прогонки решаем задачу (29) во всех узлах сетки ωh:
вычисляем F3, затем методом прогонки решаем задачу (29) во всех узлах сетки ωh:
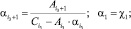
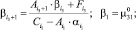
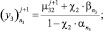
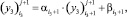
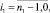
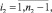
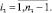 (31)
(31)
Решением является 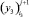 .
.
Результаты численных расчетов.
Для тестирования предложенного алгоритма численно решена задача (6) в параллелепипеде и были получены относительные погрешности вычислений εij в соответствующей норме [4]:
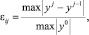
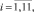 j = 1, 2, ..., j0,
j = 1, 2, ..., j0,
где j – номер итерации; i – номера клетей.
Результаты вычислений относительной погрешности εij представлены на рис. 1. При реализации вычислительного процесса каждое последующее приближение к решению точнее предыдущего, т.е. погрешность εij с каждой итерацией уменьшается. Итак, итерационный процесс сходится.
Разработанный алгоритм решения задачи температурных режимов учитывает изменения температуры непосредственно в прокатной клети и межклетевом промежутке в линии прокатного стана. Алгоритм может применяться для расчета распределения температуры различных прокатываемых материалов на любом типе сортового прокатного стана.
Программа, реализующая алгоритм решения задачи распределения температурного поля металлической катанки по клетям прокатного стана, написана на языке Fortran Pover Station 4.0 [5]. Для расчета в качестве исходных данных были использованы литературные данные.
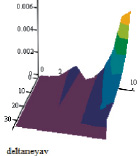
Рис. 1. Результаты вычисления относительной погрешности
В результате расчета было получено: трехмерное поле температур. Приведены результаты исследований температурного поля металлической катанки из сплава ВТ6.
Первоначально нагретая до температуры 950 °С заготовка подается в первую черновую клеть, после прокатки в клети поверхность полосы охлаждается до температур, находящихся в диапазоне 904–949 °С. На рис. 2 показано поперечное сечение раската после пятой клети, где температура поверхности раската, контактирующей с валком, за счет теплопередачи понижается до 880 °С, в результате большей пластической деформации углов заготовки и большего деформационного разогрева видно меньшее падение температуры – до 915 °С. Боковые стороны, контактирующие только с окружающей средой, охлаждаются до температуры 938 °С.
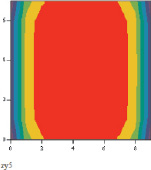
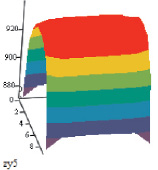
Рис. 2. Поперечное сечение раската после пятой клети
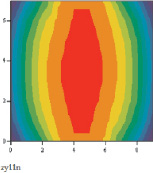
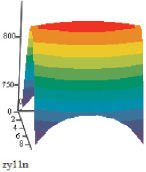
Рис. 3. Поперечное сечение раската после одиннадцатой клети
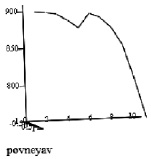
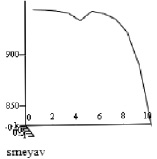
Рис. 4. Графики изменения температуры полосы по проходам, полученные в результате расчета с помощью неявной ЛОС (соответственно температура поверхности и центральной части раската)
Теоретически примем, что после пяти проходов в клети полосу режут на мерные длины, остужают, а затем снова нагревают до температуры 950 °С. Далее полосу прокатывают в группе клетей за 6 проходов, т.е. с 6 по 11 клетей. Результаты поперечного сечения раската после 11 клети показаны на рис. 3.
По теории обработки металлов давлением для получения требуемой однородной структуры необходимо добиться равномерной температуры по сечению катанки. Как видно на рис. 3, это условие выполняется, хотя осуществить это условие практически невозможно.
Полученные в результате расчета по неявной локально-одномерной схеме значения температуры раската по различным участкам прохода представлены на рис. 4.
Как показывают исследования, структуры центра и поверхности катанки отличаются, что вызвано перепадом температуры около 50 °С и сохраняется условие нагрева полосы до 950 °С на входе в 1-ую и 6-ую клети, т.е. графики изменения температуры точно описывают процесс деформации металлической катанки.
Выводы
Созданный алгоритм решения температурной задачи позволяет получить трехмерное температурное поле полосы в многоклетевом прокатном стане, проводить эксперименты, меняя те или иные факторы, влияющие на прочность и пластичность деформируемого металла, в том числе форму калибровки, не прибегая к дорогостоящим натурным экспериментам.
Проверка точности и сравнительный анализ расчета температурных полей проката дает возможность использования приведенного алгоритма локально-одномерных схем при сортовой прокатке.
Рецензенты:
Казиев Г.З., д.т.н., профессор, менеджер лаборатории больших данных, АО «Национальные информационные технологии», г. Астана;
Шарипов Б.Ж., д.п.н., профессор, главный эксперт, АО «Национальный инфокоммуникационный холдинг “Зерде”», г. Астана.



