Известно, что паразитный эхотракт дуплексной системы передачи сообщений обладает «памятью». «Память» эхотракта обусловлена тем, что его импульсная реакция имеет некоторую длительность. Форма и длительность импульсной реакции могут быть различными, поскольку они определяются множеством факторов (схемой дифференциальной системы, степенью согласования выходных параметров дифференциальной системы с входными параметрами ненагруженного канала связи и т.д.). В качестве примера на рис. 1 изображена одна из возможных форм импульсной реакции эхотракта, образованного дифференциальной системой.
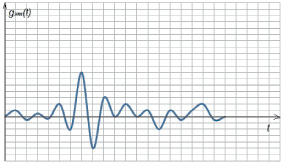
Рис. 1. Импульсная реакция эхотракта диффсистемы
При условии, что эхотракт является линейной системой, эхосигналы Sэ(t) на выходе эхотракта можно рассчитать посредством интеграла свёртки:
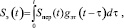(1)
где Sпер(τ) – сигналы передатчика; gэт(t) – импульсная реакция эхотракта.
Представляя сигналы передатчика в виде суммы его квадратурных компонент Sпер sin(t) и Sпер cos(t), выражение (1) можно представить в виде
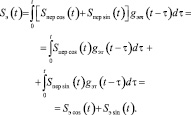(2)
Следует заметить, что слагаемые Sэ sin(t) и Sэ cos(t) в общем случае не являются ортогональными, так как ортогональность сохраняют на выходе линейной системы только сигналы, описываемые разными собственными векторами матрицы оператора паразитного эхотракта, а Sпер sin(t) и Sпер cos(t) такими сигналами в общем случае не являются. Длительность Sэ(t) вследствие эхотракта всегда превышает длительность передаваемых сигналов, что приведет к появлению межсимвольной интерференции эхосигналов. В случае если межсимвольная интерференция существенна, необходимо учитывать ее наличие и использовать алгоритмы компенсации эха, учитывающие наличие межсимвольной интерференции такой эхокомпенсации.
Далее рассмотрим ситуацию, когда передатчик реализует алгоритмы квадратурной амплитудной модуляции (КAM), которая представляет собой разновидность многопозиционной амплитудно-фазовой модуляции. Этот выбор обусловлен распространенностью КAM в современных высокоскоростных системах передачи сообщений.
КAM-модулированный сигнал может быть записан в виде следующего выражения:
Sпер(t) = Im∙cos(2πft) + Qm∙sin(2πft), (3)
где f – частота несущей; Im, Qm – амплитуды квадратурных компонентов; m – значность модуляции.
На рис. 2 изображены сигнальные созвездия КAM для разной значности модуляции: m = 2, m = 4, m = 5, m = 6.
Амплитуды квадратурных составляющих I и Q принимают дискретные значения ±1; ±3; ±5; ±7 и т.д.
В качестве примера на рис. 3 изображена структурная схема модулятора КAM-16.
Передаваемый информационный цифровой сигнал от источника сообщений поступает в регистр (Р), затем в преобразователь кода (ПК), где формируется бинарный однополярный сигнал, подвергающийся скремблированию в скремблере (СКР). После скремблера сигнал разделяется в делители потока (ДП1) на два потока (1П и 2П), каждый из которых затем делится ещё на два потока в делителях потока ДП2 и ДП3. Эти потоки пронумерованы цифрами 3, 4 и 5, 6 соответственно. В цифро-аналоговом преобразователе (ЦАП) происходит формирование 4-уровневых модулирующих сигналов квадратурных каналов.
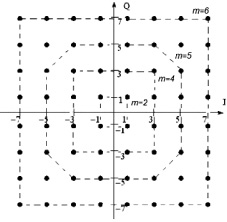
Рис. 2. Сигнальные созвездия КAM при различных значениях m
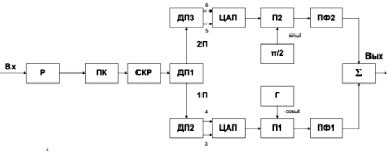
Рис. 3. Структурная схема модулятора КAM-16
При этом для каждого из возможных сочетаний 4-х входных двоичных символов (квадробитов) вырабатывается определённый уровень сигнала на выходе ЦАП. Таблица соответствия квадробитов и величин амплитуд модулирующих сигналов I и Q приведена ниже.
Таблица 1
Соответствия квадробитов и величин амплитуд модулирующих сигналов I и Q для QAM-16
|
Квадробиты |
I |
Q |
Квадробиты |
I |
Q |
||||||
|
0 |
1 |
0 |
1 |
3 |
3 |
1 |
0 |
0 |
1 |
–1 |
3 |
|
0 |
1 |
0 |
0 |
3 |
1 |
1 |
0 |
0 |
0 |
–1 |
1 |
|
0 |
1 |
1 |
0 |
3 |
–1 |
1 |
0 |
1 |
0 |
–1 |
–1 |
|
0 |
1 |
1 |
1 |
3 |
–3 |
1 |
0 |
1 |
1 |
–1 |
–3 |
|
0 |
0 |
0 |
1 |
1 |
3 |
1 |
1 |
0 |
1 |
–3 |
3 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
–1 |
1 |
1 |
1 |
0 |
–1 |
–1 |
|
0 |
0 |
1 |
1 |
1 |
–3 |
1 |
1 |
1 |
1 |
–3 |
–3 |
В перемножителях П1 и П2 происходит умножение 4-уровневых сигналов I и Q на квадратурные поднесущие. Полосовые фильтры ПФ1 и ПФ2 производят выделение тех спектральных составляющих амплитудно-модулированных сигналов, которые выходят за пределы отведённой полосы частот.
Теперь проанализируем процесс межсимвольной интерференции на выходе эхотракта с импульсной реакцией gэт(t).
Пусть на i-м единичном интервале времени длительностью τ0 передаётся сигнал:
Si пер(t) = Im i∙cos ωt + Qm i∙sin ωt. (4)
Тогда для эхосигнала на выходе эхотракта можно записать
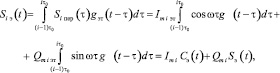(5)
где Сэ(t) и Sэ(t) – сигналы на выходе эхотракта, порождаемые импульсами cos ωt и sin ωt, поступающими на вход эхотракта.
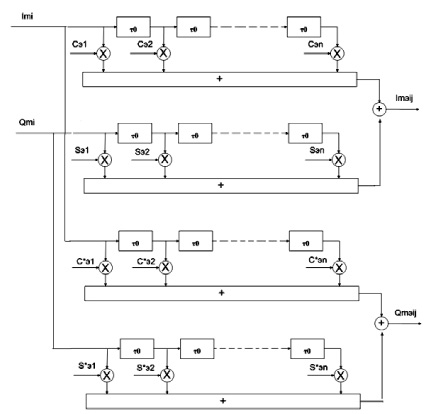
Рис. 4. Эквивалентная схема эхотракта с корреляторами для дискретных моментов времени
Пусть в схеме после дифференциальной системы включены два коррелятора с опорными сигналами cos ωt и sin ωt и длительностью интервала интегрирования τ0. Эти корреляторы разлагают сумму эхосигнала и принимаемого сигнала на квадратурные составляющие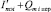 
и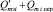 
. Вследствие памяти эхотракта длительность сигналов Сэ(t) и Sэ(t) будет больше τ0. Тогда количество результатов обработки сигналов Сэ(t) и Sэ(t) корреляторами будет равно
(6)
где τвых – длительность Сэ(t) и Sэ(t); при этом τвых = τ0 + τэт (τэт – длительность импульсной реакции эхотракта).
Квадратные скобки означают операцию округления до ближайшего большего целого числа.
Таким образом, на выходе корреляторов будет наблюдаться последовательность величин Imэ i j и Qmэ i j:
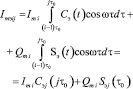(7)
и
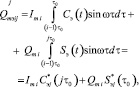(8)
где j = 1, 2, …, n.
Для дискретных моментов времени tj = jτ0 модель эхотракта с корреляторами на его выходе будет следующей, той которая изображена на рис. 4.
Как следует из этой модели, пара чисел Im i и Qm i превращаются в две последовательности чисел Im i j и Qm i j, каждая из которых имеет длину, равную n. С другой стороны, в формировании каждой пары чисел Imэ i и Qmэ j участвуют n пар чисел
{I(m(i–n)), Q(m(i–n))}, {I(m(i–n–1)), Q(m(i–n–1))};
{I(m(i–n–2)), Q(m(i–n–2))}, …, {Imi, Qmi}.
При этом можно записать
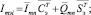(9)
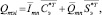(10)
где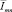 
– вектор-строка, составленная из n чисел Imi, Im(i–1), …, I(m(i–n)); 
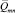– вектор-строка, составленная из n чисел Qmi, Qm(i–1), …, Q(m(i–n)); 
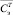– вектор-столбец, составленный из чисел Сэ1, Сэ2,…, Сэn; 
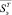– вектор-столбец, составленный из чисел Sэ1, Sэ2,…, Sэn; 
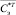– вектор-столбец, составленный из чисел 
; 
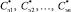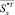– вектор-столбец, составленный из чисел 
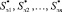; Т – знак транспонирования вектор-строки в вектор-столбец.
Как было показано выше, в формировании пары величин Imэ i и Qmэ j на выходе корреляторов, подключённых к выходу диффсистемы, участвует последовательность из n ранее переданных сигналов Si пер(t), S(i–1) пер(t), …, S(i–n) пер(t), каждый из которых однозначно представлен парой чисел {Imi, Qmi}; {I(m(i–1)), Q(m(i–1))}, …, {I(m(i–n)), Q(m(i–n))}. Эта последовательность пар чисел может быть отображена вектором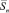 
в пространстве с 2n измерениями. С учётом того, что каждая из n координатных осей отображает 2m возможных векторов сигналов, за каждым из этих 2m векторов следует любой из 2m векторов, общее число вариантов вектора 
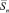будет равно 2mn.
В качестве координат вектора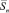 
можно рассматривать числа, составляющие вышеперечисленные пары чисел. Таким образом, каждый вектор 
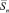согласно (9) будет порождать на выходах корреляторов, подключённых к выходу диффсистемы, две величины Imэ i и Qmэ i..
В качестве примера в табл. 2 приведены все возможные варианты векторов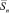 
для m = 2 и n = 2. Векторы заданы значениями Imi, Im(i–1) и Qmi, Qm(i–1).
В табл. 3 представлены соответствующие величины Imэi и Qmэi, рассчитанные для конкретных значений Сэ1 = 0,2; Сэ2 = 0,1; Sэ1 = 0,1; Sэ2 = 0,05;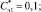 
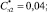
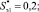
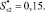
Множество векторов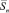 
можно разбить на два подмножества противоположно направленных векторов. Каждая пара противоположно направленных векторов, очевидно, является парой параллельных векторов, для которых выполняется инвариант аффинной группы преобразований, описывающих преобразования передаваемых сигналов в паразитном эхотракте: если два вектора, отображающих группу из n передаваемых сигналов, параллельны, то отношение длин их векторов будет равно отношению длин векторов соответствующих им эхосигналов (при этом вектора эхосигналов также будут параллельны).
Таблица 2
Варианты векторов 
для m = 2 и n = 2
Это инвариантное соотношение можно записать следующим образом:
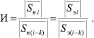(11)
Таблица 3
Величины эха на выходах корреляторов
|
Imэ i |
Qmэ i |
|
0,49 |
0,49 |
|
0,35 |
0,19 |
|
0,25 |
0,41 |
|
0,15 |
0,11 |
|
0,25 |
0,09 |
|
0,15 |
–0,21 |
|
0,05 |
0,01 |
|
–0,05 |
–0,29 |
|
0,05 |
0,29 |
|
–0,05 |
–0,01 |
|
–0,15 |
0,21 |
|
–0,25 |
–0,09 |
|
–0,15 |
–0,11 |
|
–0,25 |
–0,41 |
|
–0,35 |
–0,19 |
|
–0,45 |
–0,49 |
Здесь k обозначает количество единичных интервалов, отделяющих две последовательности передаваемых сигналов, отображаемых параллельными векторами. Вектор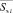 
и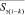 
представлены парами чисел {Imi, Qmi} и {I(m(i–k)), Q(m(i–k))}.
Из (11) следует, что
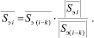(12)
Соотношение (12) показывает, каким образом можно вычислить оценку вектора эхосигнала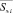 
, используя для этого образц вектора предыдущего эхосигнала 
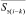и отношение длин векторов, отображающих группу передаваемых сигналов, обладающих свойством подобия, проявляющееся свойством параллельности соответствующих им векторов). Вычисленная оценка вектора эхосигнала может быть использована для компенсации эха пути вычитания её из вектора реального эхосигнала.
Описанный способ компенсации эха в условиях межсимвольной интерференции эхосигналов может быть реализован следующей структурной схемой, изображенной на рис. 5.
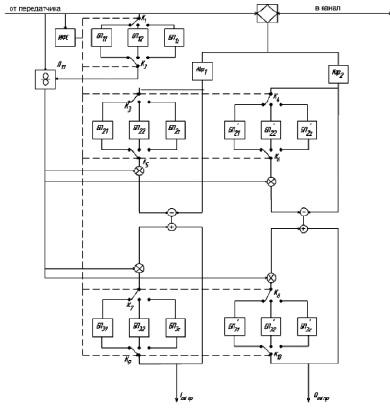
Рис. 5. Схема инвариантного эхокомпенсатора с квадратурными каналами обработки сигналов
Рецензенты:
Рогулина Л.Г., д.т.н., профессор кафедры «Радиотехнические устройства» СибГУТИ, г. Новосибирск;
Сединин В.И., д.т.н., профессор, заведующий кафедрой «Системы автоматизированного проектирования», СибГУТИ, г. Новосибирск.