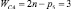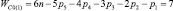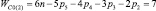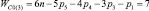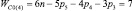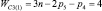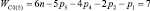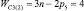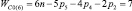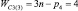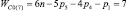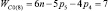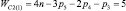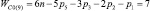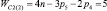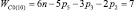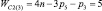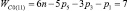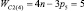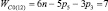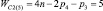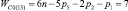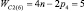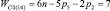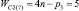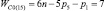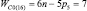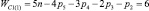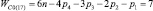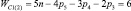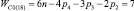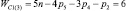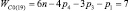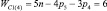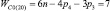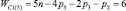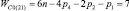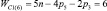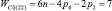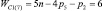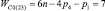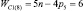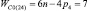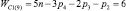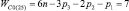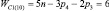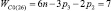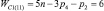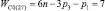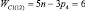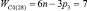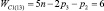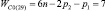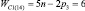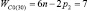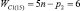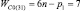В работе [1] одного из авторов настоящей статьи были обоснованы и показаны подходы к построению всеобщей (универсальной) классификации механизмов, базирующиеся на накопленных к настоящему времени знаниях о механических системах, используемых в практике машиностроения. Согласно этой классификации механизмы могут отличаться друг от друга по принадлежности их к ассуровым и неассуровым; по видам в зависимости от сложности базисного звена механизма; по их семействам в соответствии с теорией В.В. Добровольского о числе общих накладываемых на весь механизм связей; по классам и по порядкам.
В настоящей статье на основе [4] рассматривается задача о создании всего многообразия механизмов второго вида различных семейств.
Математическая модель строения механизмов второго вида
Одним из основополагающих принципов универсальной классификации является понятие видов механизмов. Это понятие определяется сложностью наиболее сложного – базисного звена, входящего в кинематическую цепь и называемого τ-угольником или τ-вершинником. Число геометрических элементов – кинематических пар базисного звена τ определяет вид механизмов. Двухпарные базисные звенья (τ = 2) образуют механизмы второго вида, трехпарные – третьего вида и т.д. Согласно [4] все кинематические цепи через параметр τ описываются системой двух уравнений, независимо определяющих сумму всех используемых в цепи кинематических пар (Σpk) и общего числа содержащихся в цепи подвижных звеньев (n)
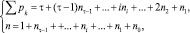 (1)
(1)
где k – класс кинематических пар, k = 1, 2, 3, 4, 5 (пара 5 класса – одноподвижная); ni – число звеньев, добавляющих в цепь по i кинематических пар; n0 – число звеньев, не добавляющих кинематических пар.
Помимо этого известно [5], что все механические системы описываются универсальной структурной формулой подвижности, обоснованной профессором В.В. Добровольским:
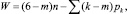 (2)
(2)
где W – подвижность кинематической цепи, а m – параметр Добровольского, как целое положительное число, определяющее количество общих наложенных на всю кинематическую цепь связей. Этот параметр может изменяться от m = 0 до m = 4. Академик И.И. Артоболевский в работе [1] обосновал целесообразность все кинематические цепи по m делить на семейства. Всего семейств механизмов пять: нулевое (m = 0), первое (m = 1), второе (m = 2), третье (m = 3) и четвертое (m = 4).
Совместное использование формулы подвижности Добровольского (2) и уравнений (1) позволило создать универсальную структурную систему
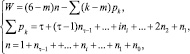 (3)
(3)
обеспечивающую возможность решать одну из основных задач теории механизмов, а именно задачу синтеза структур механизмов по задаваемым независимым параметрам τ, m, k и W.
На основании (3) обратимся к теоретическим основам создания всего многообразия механизмов второго вида, т.е. таких, наиболее сложным звеном в которых является двухпарное. Эта частная задача синтеза структур механизмов (W = 1) второго вида (τ = 2) сводится к исследованию их математической модели
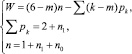 (4)
(4)
и формулируется так – найти полный состав всех возможных кинематических цепей, удовлетворяющих условиям системы (4).
Для решения поставленной задачи воспользуемся известным методом построения свободных замкнутых кинематических цепей, разработанным М. Грюблером применительно к плоским рычажным механизмам [2, 3, 7], то есть найдем все возможные замкнутые свободные цепи второго вида всех пяти семейств с одной внутренней подвижностью, из которых далее путем последовательной остановки звеньев по одному может быть найдено все многообразие механизмов второго вида. Под свободными цепями понимаются такие, которые не имеют связей с неподвижным звеном – стойкой.
Обоснование подходов к поиску свободных замкнутых кинематических цепей (СЗКЦ) второго вида
Универсальная формула В.В. Добровольского (2) для одноподвижных механизмов (W = 1) записывается в виде
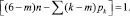 (5)
(5)
Освободим эту цепь от неподвижной стойки, т.е. включим её (стойку) в число подвижных звеньев, обратив эту цепь в свободную. При этом число звеньев цепи увеличится на одно, т.е. станет равным (n + 1). Цепь станет свободной в любом рассматриваемом пространстве m. Изменится в этом случае и подвижность цепи, она станет равной WCm
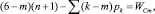 (6)
(6)
где Cm означает С – свободная замкнутая кинематическая цепь (СЗКЦ), а m – определяет семейство (0, 1, 2, 3, 4) цепи.
Раскроем в (6) скобки и получим
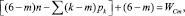 (7)
(7)
откуда с учетом (5) найдем, что
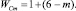 (8)
(8)
Таким образом, подвижность всех свободных замкнутых кинематических цепей (СЗКЦ) различных семейств (m = var) вполне определенно описывается формулой (8). Свободные цепи нулевого семейства (m = 0) согласно (8) обладают подвижностью WC0 = 7, первого семейства – WC1 = 6, второго семейства – WC2 = 5, третьего семейства – WC3 = 4 и четвертого семейства – WC4 = 3. В число этих подвижностей входит одна дополнительная внутренняя подвижность между звеньями каждой из цепей.
Система (4) для свободных замкнутых цепей с учетом (7) примет вид
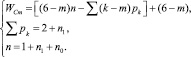 (9)
(9)
Основываясь на том, что все свободные замкнутые кинематические цепи второго вида содержат в своем составе по n двухпарных звеньев, можно утверждать, что удвоенное число кинематических пар в них 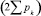 независимо от классов пар равно произведению двух пар каждого звена цепи на число звеньев n цепи (2n), т.е.
независимо от классов пар равно произведению двух пар каждого звена цепи на число звеньев n цепи (2n), т.е. 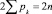 [6], откуда следует с очевидностью, что в таких цепях всегда
[6], откуда следует с очевидностью, что в таких цепях всегда
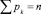 . (10)
. (10)
Это условие позволяет приравнять правые части второго и третьего уравнений системы (9) и доказать, что все такие цепи могут быть построены с использованием звеньев n0 = 1, т.е. включением в цепь одного звена, не добавляющего кинематических пар.
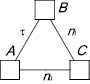
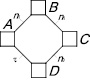
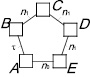
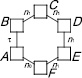
Обобщенная схема свободной замкнутой кинематической цепи второго вида показана на рис. 1. Эта цепь построена от базисного звена (τ = 2) путем последовательного присоединения звеньев n1, добавляющих в цепь по одной кинематической паре, и звена n0, замыкающего цепь.
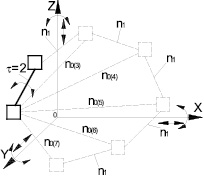
Рис. 1. Общий вид свободных замкнутых кинематических цепей второго вида
«Квадратами» на рис. 1 показаны связи – виртуальные кинематические пары между звеньями. Обозначение n0(i) означает, что это n0 относится к i-звенным механизмам. Согласно (9) и (10) всего может быть построено пять СЗКЦ второго вида с виртуальными парами, а именно трехзвенные (n = 3, 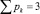 , n1 = 1 и n0 = 1), четырехзвенные (n = 4,
, n1 = 1 и n0 = 1), четырехзвенные (n = 4, 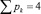 , n1 = 2 и n0 = 1), пятизвенные (n = 5,
, n1 = 2 и n0 = 1), пятизвенные (n = 5, 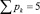 , n1 = 3 и n0 = 1), шестизвенные (n = 6,
, n1 = 3 и n0 = 1), шестизвенные (n = 6, 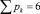 , n1 = 4 и n0 = 1) и семизвенные (n = 7,
, n1 = 4 и n0 = 1) и семизвенные (n = 7, 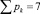 , n1 = 5 и n0 = 1). При создании полного многообразия СЗКЦ на месте виртуальных кинематических пар должны быть использованы реальные пары, удовлетворяющие условиям заданного семейства и требуемого относительного движения между звеньями рассматриваемых цепей.
, n1 = 5 и n0 = 1). При создании полного многообразия СЗКЦ на месте виртуальных кинематических пар должны быть использованы реальные пары, удовлетворяющие условиям заданного семейства и требуемого относительного движения между звеньями рассматриваемых цепей.
Прежде всего, обратимся к семействам цепей, имея в виду первое уравнение системы (9) и разделим их на подсемейства (табл. 1) в зависимости от ненулевых значений чисел пар pk.
Так как кинематические цепи четвертого семейства (m = 4) могут создаваться с использованием лишь кинематических пар р5, то это семейство содержит в своем составе единственное подсемейство. В третьем семействе (m = 3) возможны к использованию как кинематические пары р5, так и пары р4, а потому это семейство может быть разделено на подсемейства, а именно: с ненулевыми значениями пар р5 и р4, только с парами р5 и только с парами р4, т.е. на три подсемейства. По той же логике могут быть разделены цепи второго семейства (m = 2) – на семь подсемейств, первого семейства (m = 1) – на пятнадцать, а нулевого семейства (m = 0) – на тридцать одно подсемейство. Формулы подвижности всех этих подсемейств приведены в табл. 1.
Каждое подсемейство табл. 1 имеет общее обозначение Сm(i), что означает С – свободная кинематическая цепь, не имеющая соединения со стойкой; m – семейство механизмов по И.И. Артоболевскому; i – порядковый номер подсемейства внутри семейства.
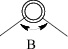
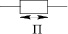
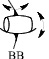
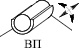
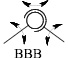
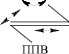
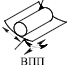
Что же касается реальных кинематических пар, то они различаются по классам, т.е. по числу относительных независимых движений звеньев на одноподвижные (р5), двухподвижные (р4), трехподвижные (р3), четырехподвижные (р2), пятиподвижные (р1) и по составам таких движений. Если обозначить относительные движения звеньев по осям декартовой системы координат как В – вращательное и П – поступательное, то всего таких составов движений четырнадцать. Кинематических пар р5 две – В и П, пар р4 три – ВВ, ПВ и ВП, пар р3 пять – ВВВ, ПВВ, ППВ, ВПВ и ВПП, пар р2 три – ВПВВ, ВППВ, ВПВП и пар р1 одна – ВПВПВ. Все одноконтактные кинематические пары приведены в табл. 2.
Таблица 1
Полный состав подсемейств свободных замкнутых кинематических цепей
|
m = 4 |
m = 0 |
|
|
|
|
|
|
|
|
|
|
m = 3 |
|
|
|
|
|
|
|
|
|
|
|
m = 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2
Полный состав одноконтактных кинематических пар механических систем
|
p5 |
|
|
p4 |
|
|
p3 |
|
|
p2 |
|
|
p1 |
|
В этих парах соприкосновения звеньев происходят в одной точке, по одной линии или по одной поверхности.
Свободные замкнутые кинематические цепи второго вида могут создаваться лишь в тех подсемействах цепей (табл. 1), где будет выполняться равенство
HСm = SСm, (11)
где под HСm – будем принимать общее количество подвижностей в цепи, выраженное из первой формулы системы (9)
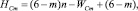 (12)
(12)
что с учетом (8) преобразуется в выражение
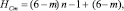 (13)
(13)
а под SСm – общую сумму связей цепей, в виде
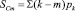 (14)
(14)
Равенство (11) с учетом (13) и (14) может быть преобразовано в выражение
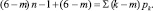 (15)
(15)
Из 57 подсемейств (табл. 1) свободные замкнутые кинематические цепи второго вида могут быть реализованы только в тех, где равенство (15) выполняется. Алгоритм поиска подсемейств СЗКЦ выполняется следующим образом: в формуле (13) задается значение n и находится ряд связанных с ним значений HCm (для всех семейств m). Общая сумма связей SCm (14) определяется кинематическими парами, которые могут принимать только целочисленные и положительные значения. Общее количество кинематических пар известно из формулы (10).
В табл. 3 представлены подсемейства свободных замкнутых кинематических цепей второго вида, а также необходимые комбинации кинематических пар, удовлетворяющие условию (15).
Задача сводится к тому, чтобы разбить полученное в (13) значение HCm на определенное количество целых частей. Коэффициенты при кинематических парах являются числами, на которые можно разбить HCm. Так в нулевом семействе формула (14) выглядит так 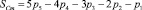 , в этом случае HCm может состоять из чисел 5, 4, 3, 2 и 1. В случае четвертого семейства SCm = p5, HCm может состоять только из единиц.
, в этом случае HCm может состоять из чисел 5, 4, 3, 2 и 1. В случае четвертого семейства SCm = p5, HCm может состоять только из единиц.
Таблица 3
Полный состав свободных замкнутых кинематических цепей второго вида
|
n m |
n = 3 |
n = 4 |
n = 5 |
n = 6 |
n = 7 |
|
m = 4 |
I С4 при р5 = 3 |
||||
|
m = 3 |
II С3(1) при р5 = 2 и р4 = 1 |
XII С3(2) при р5 = 4 |
|||
|
m = 2 |
III С2(2) при р5 = 1 и р4 = 2 IV С2(3) при р5 = 2 и р3 = 1 |
XIII С2(2) при р5 = 3 и р4 = 1 |
XIX С2(4) при р5 = 5 |
||
|
m = 1 |
V С1(2) при р5 = 1, р4 = 1 и р3 = 1 VI С1(7) при р5 = 2 и р2 = 1 VII С1(12) при р4 = 3 |
XIV С1(4) при р5 = 2 и р4 = 2 XV С1(6) при р5 = 3 и р3 = 1 |
XX С1(4) при р5 = 4 и р4 = 1 |
XXIII С1(8) при р5 = 6 |
|
|
m = 0 |
VIII С0(6) при р5 = 1, р4 = 1 и р2 = 1 IX С0(12) при р5 = 1 и р3 = 2 X С0(15) при р5 = 2 и р1 = 1 XI С0(20) при р4 = 2 и р3 = 1 |
XVI С0(4) при р5 = 2, р4 = 1 и р3 = 1 XVII С0(8) при р5 = 1 и р4 = 3 XVIII С0(14) при р5 = 3 и р2 = 1 |
XXI С0(8) при р5 = 3 и р4 = 2 XXII С0(12) при р5 = 4 и р3 = 1 |
XXIV С0(8) при р5 = 5 и р4 = 1 |
XXV С0(16) при р5 = 7 |
Из табл. 3 следует, что СЗКЦ второго вида могут быть образованы во всех пяти семействах при общем количестве звеньев от трех до семи. Трехзвенные цепи второго вида образуются во всех пяти семействах, четырехзвенные – во всех кроме четвертого, пятизвенные – во втором, первом и нулевом семействах, шестизвенные – в первом и нулевом, семизвенная цепь образуется только в нулевом семействе. Общее количество решений – двадцать пять.
Алгоритм поиска структур механизмов второго вида
Полученные в табл. 3 подсемейства и сочетания кинематических пар, а также соотношения, взятые из рис. 1, преобразованы в свободные замкнутые кинематические цепи второго вида. Все последовательности СЗКЦ схематично изображены ниже на рис. 2–6.
|
|
m |
Подсемейство |
A, B, C |
Номер цепи |
|
4 |
– |
р5, р5, р5 |
С(3)4 |
|
|
3 |
1 |
р5, р4, р5 |
С(3)3–1 |
|
|
2 |
2 |
р5, р4, р4 |
С(3)2–2 |
|
|
2 |
3 |
р5, р3, р5 |
С(3)2–3 |
|
|
1 |
2 |
р5, р4, р3 |
С(3)1–2 |
|
|
1 |
7 |
р5, р2, р5 |
С(3)1–7 |
|
|
1 |
12 |
р4, р4, р4 |
С(3)1–12 |
|
|
0 |
6 |
р5, р4, р2 |
С(3)0–6 |
|
|
0 |
12 |
р5, р3, р4 |
С(3)0–12 |
|
|
0 |
15 |
р5, р1, р5 |
С(3)0–15 |
|
|
0 |
20 |
р4, р4, р3 |
С(3)0–20 |
Рис. 2. Трехзвенные СЗКЦ второго вида
Каждой СЗКЦ задан порядковый номер, состоящий из четырех цифр. Литера С обозначает свободную кинематическую цепь, цифра в скобках определяет количество звеньев СЗКЦ, вторая цифра номера определяет семейство, третья цифра – подсемейство и четвертая цифра (если она есть) характеризует различия в последовательности расположения кинематических пар.
Семизвенные цепи второго вида структурно описываются подсемейством 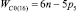 . На рис. 6 изображена семизвенная замкнутая кинематическая цепь. Одним из практических решений этой цепи является известный пространственный шарнирный семизвенный механизм.
. На рис. 6 изображена семизвенная замкнутая кинематическая цепь. Одним из практических решений этой цепи является известный пространственный шарнирный семизвенный механизм.
Таким образом, с учетом перестановок кинематических пар общее количество СЗКЦ второго вида увеличилось: трехзвенных – одиннадцать, четырехзвенных – девять, пятизвенных – пять, шестизвенных – две и одна семизвенная цепь. Всего СЗКЦ второго вида – двадцать восемь.
Практическое применение результатов исследования
Практическое применение результатов исследования, проведенного в настоящей статье, позволяет решать задачи структурного синтеза механизмов второго вида.
В качестве примера рассмотрена задача структурного синтеза механизмов со следующими параметрами: общее количество звеньев n = 4, кинематических пар <<dvornik81.wmf>>, семейство m = 0. Эти параметры соответствуют трем возможным комбинациям свободных замкнутых кинематических цепей второго вида, приведенных на рис. 3 – С(4)0–4–1, С(4)0–4–2 и С(4)0–8.
|
|
m |
Подсемейство |
A, B, C, D |
Номер цепи |
|
3 |
2 |
р5, р5, р5, р5 |
С(4)3–2 |
|
|
2 |
2 |
р4, р5, р5, р5 |
С(4)2–2 |
|
|
1 |
4 |
р4, р5, р5, р4 или р4, р5, р4, р5 |
С(4)1–4–1 или С(4)1–4–2 |
|
|
1 |
6 |
р3, р5, р5, р5 |
С(4)1–6 |
|
|
0 |
4 |
р4, р3, р5, р5 или р4, р5, р3, р5 |
С(4)0–4–1 или С(4)0–4–2 |
|
|
0 |
8 |
р4, р4, р4, р5 |
С(4)0–8 |
|
|
0 |
14 |
р2, р5, р5, р5 |
С(4)0–14 |
Рис. 3. Четырехзвенные СЗКЦ второго вида
|
|
m |
Подсемейство |
A, B, C, D, E |
Номер цепи |
|
2 |
4 |
р5, р5, р5, р5, р5 |
С(5)2–4 |
|
|
1 |
4 |
р5, р5, р4, р5, р5 |
С(5)1–4 |
|
|
0 |
8 |
р5, р4, р4, р5, р5 или р5, р4, р5, р4, р5 |
С(5)0–8–1 или С(5)0–8–2 |
|
|
0 |
12 |
р5, р5, р3, р5, р5 |
С(5)0–12 |
Рис. 4. Пятизвенные СЗКЦ второго вида
|
|
m |
Подсемейство |
A, B, C, D, E, F |
Номер цепи |
|
1 |
8 |
р5, р5, р5, р5, р5, р5 |
С(6)1–8 |
|
|
0 |
8 |
р5, р5, р4, р5, р5, р5 |
С(6)0–8 |
Рис. 5. Шестизвенные ЗСКЦ второго вида
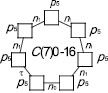
Рис. 6. Семизвенная СЗКЦ второго вида
Уточним состав кинематических пар а именно, механизм должен состоять из пар пятого р5, четвертого р4 и третьего р3 классов. Заданным условиям соответствуют две свободных цепи С(4)0–4–1 и С(4)0–4–2. Кинематические пары, которые будут использоваться в механизме, возьмем из табл. 2, к примеру пары р5 – В, р4 – ВП и р3 – ВВВ. Особенностью механизмов нулевого семейства является их способность воспроизводить все шесть движений классического декартова пространства. Для соблюдения этого условия необходимо, чтобы оси шарниров не были параллельны друг другу. В противном случае цепь получит дополнительную подвижность и будет функционировать в ущемленном пространстве (m ≠ 0).
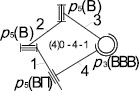
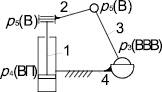
Построим свободную замкнутую кинематическую цепь С(4)0–4–1 (рис. 7, а), а в качестве стойки примем звено 4 (рис. 7, б).
В результате получен четырехзвенный механизм. Оригинальность решения подтверждена патентом РФ [6]. Уникальной особенностью представленного механизма является ведущее звено 1, которое выполнено в качестве гидроцилиндра. При работе механизма (рис. 7, б) звено 1 совершает два различных движения, при этом для функционирования механизма достаточно задать только одно из них. Этот механизм является неассуровым по своей структуре.
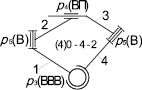
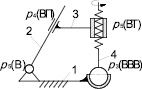
Если построить свободную замкнутую кинематическую цепь С(4)0–4–2 с теми же кинематическими парами, то получим цепь, изображенную на рис. 8, а. В качестве стойки примем звено 1, а вместо р5, соединяющей 3 и 4 звено, к примеру, можно использовать винтовую кинематическую пару р5(ВТ), тогда будет получен механизм (рис. 8, б).
Ведущим звеном является винт 4, при этом все остальные звенья механизма перемещаются вполне определенно.
Таким образом, на конкретном примере доказано, что результаты проведенного исследования можно использовать при проектировании механизмов второго вида, при этом нет необходимости проводить дополнительное исследование подвижности кинематической цепи. Любой механизм, созданный при помощи описанной в статье методики, будет обладать единичной подвижностью вне зависимости от ведущего и звена, принимаемого за неподвижное.
а б
Рис. 7. Преобразование СЗКЦ (4)0–4–1 (а) в механизм (б): а – свободная замкнутая цепь; б – полученный механизм
а б
Рис. 8. Преобразование СЗКЦ (4)0–4–2 (а) в механизм (б): а – свободная замкнутая цепь; б – полученный механизм
Заключение
Задачу структурного синтеза механизмов второго вида можно условно разбить на три этапа. На первом этапе синтез механизмов второго вида проходит по заданным параметрам, т.е. решается универсальная структурная система. Её решением являются сочетания кинематических пар, из которых состоят рассматриваемые механизмы. На втором этапе структурного синтеза составляются свободные замкнутые кинематические цепи, которые схематично изображают взаимное расположение полученных сочетаний кинематических пар. На завершающем этапе структурного синтеза механизмов условные классы кинематических пар заменяются технически реализуемыми удерживающими сочленениями звеньев, а также выбирается неподвижное звено.
Рецензенты:
Степанов А.В., д.т.н., профессор кафедры информатики и вычислительной техники, Новокузнецкий институт (филиал), Кемеровский государственный университет, г. Новокузнецк;
Живаго Э.Я., д.т.н., профессор кафедры технической механики и графики, ФГБОУ ВПО «Сибирский государственный индустриальный университет», г. Новокузнецк.