Крупногабаритные подшипники скольжения нашли широкое применение в качестве опорных узлов таких агрегатов, как мельницы самоизмельчения, мельницы полусамоизмельчения, сушильные барабаны, бутары и прочее крупногабаритное вращающееся оборудование, используемое в строительной и горнорудной промышленности.
В связи с интенсивной работой агрегатов и непрерывной значительной нагрузкой на подшипники, в процессе эксплуатации возникают характерные неисправности подшипников, которые, как правило, связаны с износом и различными дефектами поверхности скольжения, в качестве антифрикционного материала которой наибольшее распространение получили баббиты – легкоплавкие антифрикционные сплавы на основе олова или свинца.
Для повышения эффективности ремонтной обработки антифрикционного слоя крупногабаритных подшипников скольжения предлагается использовать фрезерование, а для его реализации – специальный переносной станок (рис. 1), конструкция которого защищена патентом [1]. Замена традиционно используемого ручного шабрения на фрезерование обеспечивает существенное повышение производительности обработки при возможности обеспечения стабильных параметров точности выдерживаемого размера и качества обрабатываемой поверхности [2, 3].
Переносной станок содержит корпус 1, выполненный в виде двух плоских рам 2. Каждая плоская рама 2 в нижней части имеет два опорных элемента 3, выполненных в виде башмаков. Опорные элементы 3 предназначены для установки переносного станка на корпусе подшипника 4. В верхней части плоские рамы 2 соединены приводным валом 5, который опирается на подшипниковые узлы 6. Приводной вал 5 является конечным звеном кривошипно-коленного механизма 7 привода маятниковой круговой подачи. Кроме того, в привод входят редуктор 8 и электродвигатель 9. На приводном валу 5 жестко закреплена качающаяся рама 10. В нижней части рамы 10 размещен рабочий узел 11. Рабочий узел 11 имеет направляющие 12, на которых установлена подвижная каретка 13. Подвижность каретки 13 обеспечивается за счет кинематической связи ее с приводом продольного перемещения 14. Подвижная каретка 13 оснащена обрабатывающим лезвийным инструментом 15, фрезой. Обрабатывающий инструмент 15 получает рабочее движение от привода главного движения 16.


Рис. 1. Общий вид станка
В процессе проведения ремонтной обработки важной технологической задачей является обеспечение качества опорной поверхности скольжения, к которой предъявляют весьма жесткие требования. Качество поверхности скольжения обуславливает коэффициент и условия трения-скольжения, удержание смазки, износостойкость и, как следствие, обеспечение прямолинейности оси эксплуатируемого агрегата посредством минимального изменения величины зазора в подшипнике в процессе работы, а следовательно, надежность работы подшипника скольжения и эксплуатируемого агрегата в целом.
Баббит является легкоплавким пластичным материалом, поэтому его механическая обработка связана с такими явлениями, как оплавление и наростообразование. Оплавление возникает в случаях, когда температура в зоне резания превышает температуру плавления баббита. Исходя из физико-механических свойств уже при 240 °С баббиты размягчаются, интенсифицируется наростообразование и процесс резания существенно усложняется.
Для обеспечения требуемого качества обрабатываемой поверхности скольжения (точность по 8 квалитету и шероховатость Ra 1,6–3,2) процесс механической обработки баббита необходимо проводить в определенном заданном интервале технологических параметров [2]. Скорость резания и величина подачи режущего инструмента при фрезеровании баббита определяют температуру в зоне резания, формируют микрорельеф поверхности. Кинематические параметры специального оборудования, используемого при ремонтной обработке, должные обеспечивать заданные технологические параметры, в свою очередь обеспечивающие требуемое качество обрабатываемой поверхности [5].
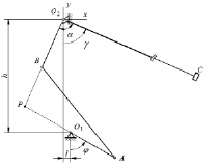
Рис. 2. Расчетная схема
Расчетная схема станка для определения кинематических параметров механизма [4], определяющих технологические режимы резания, представлена на рис. 2.
Входными параметрами для расчетов являются:
ω – угловая скорость вращения кривошипа O1A;
l1, l2, l3, l4 – длины кривошипа O1A, связующего звена AB, плеч коромысла O2B и O2C, соответственно;
α – угол при вершине коромысла;
l, h – смещение оси коромысла O2 относительно опоры O1 по горизонтали и вертикали соответственно.
Положение фрезы (точка C на рис. 2) будем определять углом γ, отсчитываемым от вертикали. При этом, когда фреза находится на правой половине обрабатываемой поверхности, угол γ будем считать положительным, когда на левой – отрицательным.
Перед тем как определять положения кривошипа O1A в зависимости от угла γ, необходимо определить пределы изменения этого угла.
Начало системы координат расположим в точке O2, направления осей показаны на рис. 2. Тогда координаты шарнира A в зависимости от угла поворота кривошипа φ определяются формулами
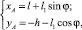 (1)
(1)
а координаты шарнира B могут быть определены из условий, что он находится на расстоянии l2 от шарнира A и на расстоянии l3 от оси коромысла O2:
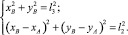 (2)
(2)
Полученная система уравнений имеет следующее решение:
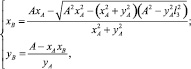 (3)
(3)
где 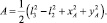 (4)
(4)
Предельные положения фрезы достигаются тогда, когда координата по оси y шарнира B – yB достигает максимума и минимума. Поскольку координата yB является непрерывной функцией угла φ, в точках экстремума должно выполняться условие
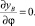 (5)
(5)
Дифференцируя первое равенство в (1), получим
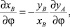 (6)
(6)
используя которое, а также формулы, вытекающие из (1):
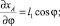
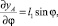 (7)
(7)
из продифференцированного второго равенства (2), найдем
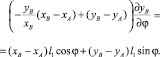 (8)
(8)
Таким образом, условие (5) выполняется, если
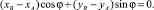 (9)
(9)
Уравнение (9) на интервале изменения угла φ от 0 до 2π имеет два решения, для каждого набора входных параметров решается численно, поскольку в нем и xA, yA, и xB yB являются функциями угла φ.
Зависимость получена при следующих значениях входных параметров:
l = 0,0049 м; h = 0,271 м; l1 = 0,12 м;
l2 = 0,274 м; l3 = 0,124 м. (10)
Полученные в результате решения уравнения (9) два значения угла φ обозначим как φi (для минимального значения угла γ) и φa (для максимального значения угла γ).
Соответствующие им значения угла γ определяются следующим образом. Уравнение прямой, на которой лежит отрезок O2B, имеет вид
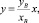 (11)
(11)
а уравнение прямой, на которой лежит отрезок O2C –
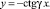 (12)
(12)
Поскольку угол между O2B и O2C – α, то
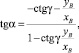 (13)
(13)
откуда следует, что
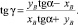 (14)
(14)
Таким образом, если вычислить xB и yB (формулы (3)) при значениях φ, равных φi и φa, по формуле (14) находятся граничные (предельные) значения угла γ – γi и γa.
Так, для значений входных факторов (10) и угла α = 90°,
φa = 12,54°; φi = 183,85°;
γa = 76,69°; γi = –79,98°. (15)
При α = 90° формула (14) может быть записана в виде
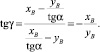 (16)
(16)
Вычислив пределы изменения угла γ – γi и γa, далее необходимо, с целью вычисления скорости подачи, вычислить, для любого значения угла γ в интервале γi ≤ γ ≤ γa соответствующее ему значение угла φ.
Задавшись значением угла γ, преобразованием формулы (16), находим
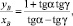 (17)
(17)
добавив к полученному уравнению первое уравнение (2), из системы двух уравнений определяем координаты точки B:
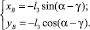 (18)
(18)
Координаты точки A определяются из системы уравнений
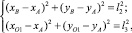 (19)
(19)
решение которой дается формулами
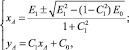 (20)
(20)
где
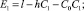
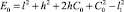 (21)
(21)
и, в свою очередь,
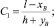
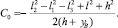 (22)
(22)
По вычисленным значениям xA и yA, являющимся функциями угла γ, определяется искомое значение угла φ по формулам, обратным формулам (1):
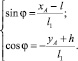 (23)
(23)
В выражении (20) знак «+» принимается при изменении угла γ от γa до γi (холостой ход) и знак «–» при изменении угла γ от γi до γa (фрезерование).
Дальнейшие расчеты – расчет скорости перемещения (величина подачи) фрезы для вычисленного угла φ, производится следующим образом:
– определяются координаты точки P (мгновенного центра скоростей звена AB):
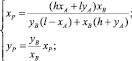 (24)
(24)
– рассчитываются расстояния от точек A и B до точки P:
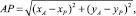
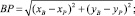 (25)
(25)
– вычисляется скорость подачи фрезы:
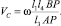 (26)
(26)
Для приведенных выше значений входных параметров и двух значений угловой скорости вращения кривошипа O1A ω = 0,021 c–1 и ω = 0,031 c–1 (n = 0,2 об/мин и n = 0,3 об/мин) на рис. 3 и 4 представлены зависимости скорости подачи фрезы VC в зависимости от угла поворота плеча O2C коромысла γ. На рис. 3 – скорость «холостого» хода, на рис. 4 – скорость подачи фрезы в процессе обработки.
Для заданного размера обрабатываемого подшипника с предельными углами –γp, γp, разработанная методика позволяет, кроме расчета скорости подачи фрезы, рассчитать «выход» фрезы за пределы обрабатываемой поверхности (для обеспечения поперечного перемещения фрезы вне обрабатываемой поверхности подшипника) и, кроме того, время нахождения фрезы вне обрабатываемой поверхности (для расчета скорости поперечного перемещения фрезы).
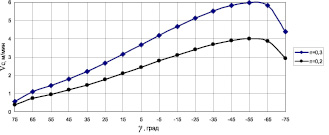
Рис. 3. График изменения скорости холостого хода
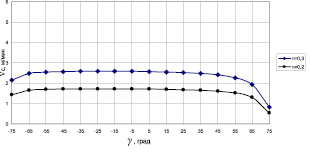
Рис. 4. График изменения подачи рабочего хода
Представленная методика кинематического анализа механизма специального станка для ремонтной обработки опорной поверхности крупногабаритных подшипников скольжения позволяет конструктивно предусмотреть необходимые технологические параметры механической обработки, обеспечивающие заданное качество обрабатываемой поверхности.
Рецензенты:
Пастухов А.Г., д.т.н., профессор, зав. кафедрой технической механики и конструирования машин, ФГБОУ ВО «Белгородский государственный аграрный университет им. В.Я. Горина», Министерства сельского хозяйства Российской Федерации; п. Майский;
Пелипенко Н.А., д.т.н., профессор кафедры прикладной геологии и горного дела факультета горного дела и природопользования, ФГАОУ ВПО «Белгородский государственный национальный исследовательский университет», г. Белгород.



