Методы акустической диагностики широко используются в современных системах интроскопии и позволяют получать информацию о пространственном распределении внутренних параметров объектов исследования, а также о протекании изучаемых процессов [9, 5]. В последнее время в ультразвуковых диагностических системах все большую роль играют методы реконструктивной томографии [6]. Это связано с прогрессом в области IT технологий, увеличением скорости обработки данных и объемов хранимой информации.
До недавнего времени большую конкуренцию томографическим методам оказывали традиционные методы ультразвуковой диагностики, основанные на методах эхо-локации, при обработке данных в режиме яркостного сканирования (B-scanning) [13]. Эти методы получили широкое распространение в медицинской диагностике (УЗИ) и неразрушающем контроле (НРК), благодаря простоте алгоритмов обработки данных и методов отображения диагностической информации [13, 2]. Для получения данных эхо-локации внутренние области объекта должны иметь большое различие акустических импедансов с четкими границами раздела. Именно такое строение исследуемого объекта позволяет получить уверенную регистрацию отраженного ультразвукового сигнала, которая необходима для контрастного восстановления его внутренней структуры.
Однако на практике часто встречаются объекты, имеющие плавную пространственную вариацию внутренних акустических параметров, что не обеспечивает возникновения отраженного сигнала, достаточного для регистрации ультразвуковой диагностической системой. Те же проблемы могут возникать в доплеровских ультразвуковых системах, традиционно основанных на обработке сигналов, отраженных от мелких частиц, движущихся в потоке [1]. Для такого типа объектов информацию о внутренних параметрах можно получить только по характеристикам проходящих УЗ-сигналов.
Более того, используя данные о времени задержки при прямом и обратном прохождении акустического сигнала, можно одновременно получить информацию о нескольких параметрах внутренней структуры исследуемого объекта, например скорости ультразвука в среде и скорости движения среды распространения. Аналогичная информация может быть получена при регистрации фазового сдвига УЗ-волны в прямом и обратном направлениях, в связи с чем объекты с плавным изменением акустических импедансов можно рассматривать в качестве фазовых объектов.
Отметим, что по полученным распределениям скоростей звука в среде распространения УЗ-волны можно построить и распределения других параметров, например, концентраций примесей [3] или локальные флуктуации температуры в однородных средах [12].
Целью данной работы является разработка алгоритма томографической реконструкции статических и динамических фазовых объектов, скоростей потоков однородных жидкостей и проведение экспериментальных исследований, подтверждающих работоспособность данного алгоритма.
Ультразвуковая томография фазовых объектов
Алгоритм томографической реконструкции. Фазовый набег акустической волны или временная задержка УЗ-сигнала являются интегралом от функции групповой скорости волны по длине траектории акустического луча.
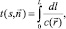 (1)
(1)
где 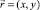 – радиус вектор;
– радиус вектор; 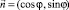 – единичный вектор в направлении УЗ пучка; s – расстояние от начала координат до луча; L – длина акустического луча; с(x,y) – скорость звука в среде распространения.
– единичный вектор в направлении УЗ пучка; s – расстояние от начала координат до луча; L – длина акустического луча; с(x,y) – скорость звука в среде распространения.
Уравнение (1) представляет собой набор одномерных проекций временных задержек УЗ сигнала, прошедшего через исследуемый объект под углом наклона φ.
Для восстановления двух параметров среды удобно использовать сумму 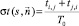 или разность
или разность 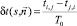 времен задержек акустических сигналов, идущих в прямом и обратном направлениях и нормированных на время распространения сигнала между приемником и излучателем в неподвижной однородной среде T0 = L/c0.
времен задержек акустических сигналов, идущих в прямом и обратном направлениях и нормированных на время распространения сигнала между приемником и излучателем в неподвижной однородной среде T0 = L/c0.
Решение интегрального (1) уравнения возможно с помощью преобразования Радона, используемого в алгоритмах реконструктивной томографии, позволяющего получить двумерные распределения параметров сечений исследуемых объектов [7].
На практике реализация преобразования Радона осуществляется методом обратных проекций (Back Projection), в котором одномерные проекции растягиваются по ортогональной координате s и суммируются по углу наклона зондирующего УЗ пучка:
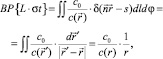 (2)
(2)
где BP{} – оператор обратного проецирования; c0 – скорость звука в однородной среде, где 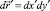 – двумерный элемент площади.
– двумерный элемент площади.
Уравнение, получающееся в результате двумерной свертки, легко решается в Фурье-пространстве с применением соответствующего фильтра пространственных частот. В целом метод получил название метода фильтрации обратных проекций (Filtered Back Projection) [11, 15]. Для восстановления пространственного распределения скорости звука в среде для объекта с центральной симметрией имеем
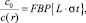 (3)
(3)
где FBP{} – оператор фильтрации обратных проекций.
Для компонент скорости потоков в среде распространения ультразвукового сигнала жидкостей необходимо учитывать угол сноса УЗ луча. Значение этого угла может быть найдено из принципа Ферма, согласно которому акустический сигнал распространяется по траектории с минимальной задержкой. Дополнительное уравнение для угла сноса позволяет разделить компоненты скорости движения среды и для потока с центральной симметрией получить (вихря жидкости):
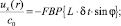
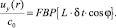 (4)
(4)
Экспериментальная установка. Для проведения ультразвуковой реконструктивной томографии фазовых объектов была разработана система, представленная на рис. 1. Фазовый объект размещается в плоской кювете прямоугольной формы 90×70 мм и толщиной 25 мм. Стенки кюветы выполнены из прозрачного пластика. На боковых гранях установлены 4 акустические антенны М9060 фирмы «АКС».
Каждая акустическая антенна имеет 16 расположенных в ряд пьезопреобразователей. Общее число каналов, по которым сигнал излучается и принимается, составляет 64; излучение и прием осуществляется многоканальной системой MultiX (производства компании М2М). Работа аппаратной части системы управляется и контролируется подсистемой, в состав которой входит программное обеспечение MultiX М2М и специальное управляющее программное обеспечение, созданное на базе платформы LabView.
Использование четырёх линейных решёток пьезопреобразователей позволяет проводить анализ любого фазового объекта, находящегося в кювете в области пересечения акустических лучей. MultiX осуществляет электронное переключение каналов, окружающих область исследования. Каждый из 64 каналов поочерёдно излучает УЗ-импульс с центральной частотой 5 МГц, и после прохождения в среде этот импульс регистрируется всеми остальными элементами [4].
Ультразвуковая томография статических фазовых объектов. На первом этапе, для оценки адекватности математической модели и методики реконструкции изображения были проведены исследования со стационарными фазовыми объектами различных размеров: точечным и объектом средней величины.
В качестве точечного объекта использовалась трубочка диаметром d = 5 мм из тонкого пластика, что исключало искажение проходящего ультразвукового луча.
Трубочка заполнена жидкостью FC-70 [10], скорость звука в данном веществе составляет C = 680 м/с, акустический импеданс равен ZFC = 1,34∙106 Па∙с/м3. Концы трубочки запаяны термоклеем, а места спайки закрыты пластилином, что исключает искажения ультразвуковой волны (рис. 2 а). Вся кювета вокруг фазового объекта заполнена водой, акустический импеданс которой принимался равным ZВ = 1,5∙106 Па∙с/м3.
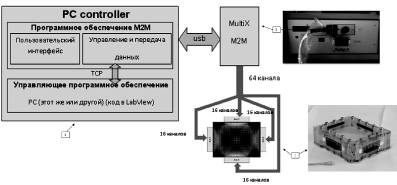
Рис. 1. Измерительная система сбора данных для проведения ультразвуковой реконструктивной томографии фазовых объектов: 1 – кювета; 2 – 64-канальная система MultiX М2М; 3 – управляющий блок

Рис. 2. Эксперименты со статическими фазовыми объектами: а – кювета с точечным объектом – трубочкой d = 5 мм; б – результат моделирования; в – восстановленное изображение; г – кювета с шариком d = 15 мм; д – восстановленное изображение
Численное моделирование осуществлялось методом построения прямых проекций лучей в геометрии кюветы [14]. Восстановление томографических изображений, как для модели, так и для экспериментальных данных, выполнялось методом обратных проекций.
На рис. 2 б представлен результат численного моделирования томографического восстановления изображения малого фазового объекта. На рис. 2 в представлен – экспериментальный результат томографии тонкой трубки, полученный при помощи созданной ультразвуковой системы. Сравнительный анализ отмасштабированных изображений показал, что расхождение не превышает 0,7…1,5 % от размера точечного объекта.
Полученные результаты позволяют утверждать, что данная информационно-измерительная система и разработанный математический аппарат для обработки сигналов позволяют восстановить изображение объекта, размеры которого существенно меньше расстояния между излучателями.
В качестве фазового объекта средней величины был выбран шарик диаметром d = 15 мм, наполненный изо-пропанолом (Propanol 2), оболочка которого была выполнена из тонкого латекса, что позволяло ультразвуковым лучам проходить через эту оболочку без искажений. Акустический импеданс изо-пропанола отличается от импеданса воды незначительно, но больше, чем у FC-70 – Za = 0,93∙106 Па∙с/м3. Скорость звука в изо-пропаноле – СРr = 1160 м/с (в воде Vзв = 1483 м/с).
На рис. 2 д представлено восстановленное изображение шарика. Анализ реальных размеров объекта и восстановленного изображения подтверждает, что они практически идентичны (расхождения составляют не более 4 %). Это даёт основание полагать, что принятая методика может использоваться и для восстановления статических фазовых объектов средней величины, размеры которых сопоставимы с расстоянием между излучателями.
Ультразвуковая томография динамических фазовых объектов. Возможность восстановления изображения подвижного объекта исследовалась также с использованием шарика с диаметром 15 мм, заполненного изо-пропанолом. Место спайки латекса закрывалось пластилином.
Движение шарика в кювете со скоростью, в пределах 0,02 м/с обеспечивалось плавным наклоном кюветы. Последовательность восстановленных изображений, полученных с интервалом 0,5 с, представлена на рис. 3 б. Анализ изображений подтверждает, что использованный подход и полученные результаты численного моделирования позволяют восстанавливать томографическое изображение малоподвижных фазовых объектов простой формы, т.е. движущихся со скоростью, много меньшей скорости звука в среде.

а б
Рис. 3. Эксперимент с динамическим фазовым объектом d = 15 мм: а – кювета с объектом; б – восстановленные изображения подвижного шарика с интервалом 0,5 с
Ультразвуковая томография бинарных жидкостей. Для томографической реконструкции использовались две несмешиваемые (бинарные) жидкости: вода и силиконовое масло (вязкость 1,5 сSt), имеющие различные физические и акустические свойства. Плотности и вязкости этих жидкостей приблизительно равны, а акустические импедансы значительно различаются (таблица).
С этими жидкостями были проведены физический и модельный эксперименты. Результаты представлены на рис. 4 а и б соответственно. На рис. 4 в показан результат восстановления изображения бинарных жидкостей, имеющих границу раздела.
Физические параметры воды и силиконового масла
|
Parameters Liquids |
Скорость звука, м/с |
Плотность, г/см3 |
Акустический импеданс, ∙106 Па∙с/м3 |
Вязкость, сСт |
|
Вода |
1483 |
0,998 |
1,5 |
1,0 |
|
Силиконовое масло |
920 |
0,853 |
0,78 |
1,5 |

а б в
Рис. 4. Определение границы раздела двух жидкостей (воды и силиконового масла): а – общий вид установки; б – модельный расчет для условий эксперимента; в – восстановленное изображение на основе экспериментальных данных
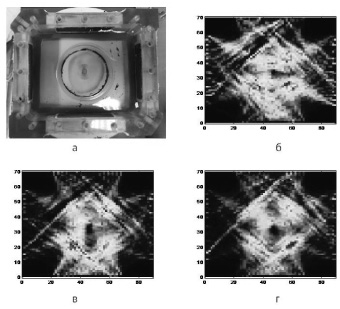
Рис. 5. Томографическая реконструкция вихревого потока: а – общий вид установки; б, в и г – восстановленные изображения распределения модуля скорости вихревого потока с интервалом в 0,5 с
Ультразвуковая томография вихревого потока однородной жидкости. На таких объектах также был проведен эксперимент с использованием метода ультразвуковой томографии. Было показано, что и в этом случае методы ультразвуковой томографии позволяют контролировать распределение скорости в потоках однородной жидкости. Для исследования возможности восстановления поля скоростей движущейся однородной жидкости кювета оснащалась магнитным импеллером, размещающимся вне области перекрытия ультразвуковых лучей. Вращение импеллера обеспечивалось генератором магнитного поля BioblockScientific AM3002. Скорость вращения импеллера составляла 1250 об/мин. Данные для томографического восстановления регистрировались с интервалом 0,5 с. На рис. 5 б, в и г чётко выражено различие распределения скоростей в потоке.
Выводы
Результаты выполненных экспериментов показали, что разработанная методика томографической реконструкции, с использованием стационарных излучателей ультразвука на плоских поверхностях, позволяет получить полное обзорное (в пределах 360°) изображение фазовых объектов [14].
Используемый алгоритм томографической реконструкции позволяет восстанавливать:
– изображения стационарных фазовых объектов с размерами более 7 % от расстояния между излучателями с точностью в пределах 4 % от размера объекта;
– изображение динамических фазовых объектов;
– изображение раздела несмешиваемых жидкостей с близкими физическими характеристиками;
– распределение скоростей вихревого потока однородной жидкости.
Следует отметить, что полученные изображения имеют ряд искажений, характерных для томографической реконструкции на первичном этапе обработки, связанных с геометрией эксперимента (в нашем случае с прямоугольным расположением приемно-передающих антенн). Необходимая коррекция обычно достигается применением адаптивной фильтрации [8], позволяющей уменьшить артефакты томографического изображения.
Поиск фильтра, соответствующего геометрии нашего эксперимента, является предметом дальнейших исследований.
Работа выполнялась в международной лаборатории LIA LEMAC/LICS в рамках Европейского проекта IRSES «PAS», при поддержке грантов РФФИ 13-02-93105-НЦНИЛ_а и 13-02-93108-НЦНИЛ_а.
Рецензенты:
Романов М.П., д.т.н., профессор, директор института кибернетики, Московский государственный университет информационных технологий, радиотехники и электроники, г. Москва;
Карп В.П., д.т.н., профессор кафедры информационных систем, Московский государственный университет информационных технологий, радиотехники и электроники, г. Москва.



