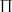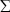Для конвертации книг и документов в электронный вид обычно используют только их текстовую часть, что позволяет хранить информацию в компактной форме и добавлять в электронные библиотеки. В то же время практически не обрабатывается часть документа, содержащая математические и химические формулы, что препятствует получению полноценного документа в электронном виде. Сложность задачи формализации описания математических формул состоит в необходимости выделения формулы среди нематематического текста, анализа ее структуры, распознавания математических символов и букв.
В настоящее время зарубежные и отечественные ученые ведут исследования в области распознавания формул, на их основе созданы системы и сервисы, решающие задачи распознавания формул, в зависимости от их вида, полностью или частично [3–5, 11, 13]. Однако, несмотря на имеющиеся успехи, следует отметить и имеющиеся недостатки. Так, в приложении InftyReader [3] не решена задача распознавания «многоэтажных формул» с индексами и степенями; в системе Freehand Formula Entry System (FFES) [13] (on-line распознавание рукописных формул) нет возможности распознавания сканированного изображения; в приложении EXTRAFOR [11] (выделение формул из текста) достигается только частичная обработка математического документа. В отечественных работах [4, 5] затронут лишь начальный этап исследований в области описания формул с помощью регулярных выражений и проведено моделирование формул с помощью графов, но нет практических результатов.
В настоящей статье представлены методы анализа математических формул произвольной сложности. Цель описанных методов заключается в выявлении и анализе межсимвольных связей, распознавании выделенных специальных математических символов и букв. Для достижения поставленной цели разработаны и реализованы следующие методы:
– метод скелетизации (позволяет производить дальнейшую обработку символа вне зависимости от толщины символа, шрифта, наклона);
– метод поиска линий и выявление отдельных символов (используется для выделения на изображении таких математических знаков, как «дробь» и разновидности знака «равно», и некоторых других математических символов (знаки интеграла, скобки, знаки арифметических и логических операций) для разбиения формулы на более простые (подформулы).
В статье выполнены экспериментальные исследования и дана оценка качества полученных результатов.
Структурный анализ математических формул и символов
Формулой будем называть выражение, имеющее следующий вид:
<левая часть> <оператор> <правая часть>, (1)
где <оператор> – это арифметическая или логическая операция или знак отношений; <левая часть> и <правая часть> – выражения (подформулы). В свою очередь подформулы, как и формула, могут иметь вид (1).
Формула состоит из символов, к которым относятся цифры, буквы латинского и греческого алфавитов, знаки арифметических и логических операций, стрелки, скобки, специальные знаки, использующиеся в математических формулах (операторы с переменным диапазоном: 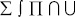 , символы, использующиеся в теории множеств:
, символы, использующиеся в теории множеств: 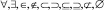 ).
).
1. Структурный анализ формулы
По своему расположению в тексте формулы делятся на два типа: однострочные, встроенные в нематематический текст (например, «…уравнение прямой имеет вид y = kx + b, где...»), и многострочные, находящиеся изолированно между частями нематематического текста, например:

В дальнейшем ограничимся рассмотрением сканированных изображений с одной формулой, предварительно выделенной из электронного документа. Первоначальным этапом анализа формулы является ее разбиение на отдельные символы. Эта задача решается при помощи программной системы ПС ИНС [7], в которой реализована схема разделения исходного изображения на изображения с отдельными символами. Система имеет развитый графический интерфейс, в котором каждый блок представляет отдельный программно реализованный модуль, который можно соединять с другими модулями посредством входных и выходных каналов. На рис. 1 представлена схема, реализующая алгоритм сегментации изображения, в результате которого будет получен набор изображений с отдельными символами.
Процесс получения на выходе серии изображений с отдельным символом формулы состоит из следующих шагов:
1) чтение (ReadImages) исходного изображения из памяти;
2) удаление фона (HistDelete) на входном цветном изображении путем анализа гистограммы. Полученное цветное изображение, в котором фон представлен alpha-каналом, подается на сегментацию;
3) сегментация (FindObjects, GetObjects) основана на маркировке связных компонент на цветном изображении. Этот метод эффективно работает на символах, состоящих из одной компоненты (например, 1, 2, А, В), а для символов из нескольких составляющих (j, i, =, %) требуется дополнительная обработка для объединения, прежде чем символы будут поданы на распознавание;
4) передача (ImageWriter) полученных сегментов формулы на следующий этап обработки, использующий на входе серию изображений.
Рассмотрим последующие шаги обработки изображения, которые были реализованы в системе ПС ИНС непосредственно автором настоящей статьи.

Рис. 1. Схема сегментации отдельных элементов формулы
2. Морфология изображений
2.1. Скелетизация
Для описания символов, представленных матрицей точек, выполняется процедура скелетизации. Скелет представляет собой плоский граф, отражающий особенности формы объекта [12]. Вершины скелета – это центры окружностей, касающихся границы фигуры в трех или более точках, а ребра – линии, состоящие из точек-центров вписанных окружностей, касающихся в двух или более точках. Для нахождения скелетов предварительно бинаризованного после сегментации изображения использован алгоритм Зонга-Суня [14]. При сканировании символа применена 8-связная структура соседства пикселей. «Перекрашиваются» в белый цвет те черные граничные точки, которые не нарушают связности оставшейся фигуры. Благодаря 8-связной области происходит последовательное закрашивание пикселей краев «север-запад» и «юг-восток». Процесс повторяется до тех пор, пока не останется пикселей, которые можно перекрасить.
Алгоритм скелетизации упрощает дальнейшую работу с изображением и устойчив к шуму. К недостаткам такого преобразования символа относятся вероятность нарушения связности и относительно большие временные затраты.
Следующий шаг состоит в поиске линий на скелетном изображении для извлечения информации о содержащихся в формуле символов дроби, отрицаний, знаков « = », «–». Если данная информация подтверждается, то выполняется исследование окружающих эти знаки символов.
2.2. Выделение линий
Для выделения линий на изображении используется преобразование Хафа [8]. Прямые описываются с помощью уравнения r = x cos θ + y sin θ при условии, что θ ∈ [0, π] и r ∈ R, где r – величина вектора от начала координат до ближайшей точки на прямой; θ – угол между этим вектором и осью координат.
Схема на рис. 2 демонстрирует в комплексе: реализацию сегментации входного изображения (рис. 3) на символы, построение бинарного изображения, приведение к скелетному изображению и выделение прямых. На выходе схемы получаем скелет входного изображения с выделенными линиями (рис. 4).

Рис. 2. Схема выделения линий на изображении
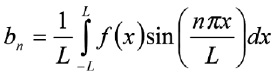
Рис. 3. Пример входного изображения
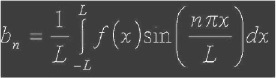
Рис. 4. Результат выделения линий на скелетизированном изображении (отмечены серым)
Распознавание символов на основе метода базовых локальных признаков
1. Структурный анализ формулы. Выделение подформул
Следующим шагом структурного анализа формулы является разбиение ее на подформулы. Разбиение формулы происходит до тех пор, пока не останется делимого на символы выражения. Каждый символ, соединяющий две подформулы, имеет свой приоритет, согласно которому определяется последовательность поиска символа в формуле (приоритет «1» – для  , приоритет «2» – для стрелок, приоритет «3» – для
, приоритет «2» – для стрелок, приоритет «3» – для 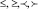 , приоритет «4» – для знаков арифметических и логических операций). Дополнительными символами соединения подформул являются: операторы с переменным диапазоном (
, приоритет «4» – для знаков арифметических и логических операций). Дополнительными символами соединения подформул являются: операторы с переменным диапазоном (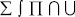 ), знак корня, горизонтальной черты и скобки.
), знак корня, горизонтальной черты и скобки.
При помощи метода базовых локальных признаков [8] формируется множество признаков распознаваемых объектов, характерных для определенного символа. В качестве множества признаков будут выступать угловые точки, найденные на символе. Распознавание объекта происходит путем сопоставления признаков модели и признаков изображения. В статье будет освещено распознавание символов с приоритетом «1» и операторов с переменным диапазоном, корня и знака горизонтальной черты.
2. Обнаружение параллельных прямых
Пусть на изображении имеется набор прямых, найденных с помощью метода Хафа [8]. Прямая Lk представлена координатами начальной точки (xk1, yk1) и конечной точкой (xk2, yk2). Для обнаружения объектов с приоритетом «1» из набора выбираются те прямые Lk, Lj, которые соответствуют следующим признакам:
– расстояние между точками (xk1, yk1) и (xk2, yk2) меньше или равно min(Lk, Lj), где Lk, Lj – длины k-й и j-й прямых;
– 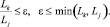
Дополнительно определяются понятия «главное равно» и «второстепенное равно». «Главное равно» соединяет две подформулы, «второстепенное равно» входит в состав подформулы. Входными данными для обнаружения параллельных прямых является предварительно промаркированное, скелетизированное бинарное изображение, на котором горизонтальным прямым присвоены метки. На рис. 5 представлен результат детектирования «главного равно», отмеченного цифрой 1, «второстепенного равно» – цифрой 2.
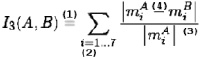
Рис. 5. Результат выделения знака «главное равно» (1), «второстепенное равно» (2), горизонтальных линий (3, 4)
3. Угловые точки как вершины графа
Поиск угловых точек как вершин графа является способом, инвариантным к аффинным преобразованиям, основан на направлении градиентов соседних пикселей. Детектор Харриса проигрывает в скорости работы по сравнению с другими алгоритмами [12], но дает точные результаты.
На вход алгоритма Харриса подается полутоновое изображение. Проход по изображению осуществляется с использованием дифференциальной маски. Определяется изменение яркости соседних пикселей в различных направлениях относительно текущего пикселя. Точка является угловой, если изменение градиента наибольшее, а сдвиг окна (относительно текущего пикселя) мал.
Каждый символ можно представить в виде графа G = (X, V), где X = (point1, point2, ..., pointn) – множество вершин графа; V = (v1, v2, ..., vn) – множество ребер графа. На рис. 6 представлен результат работы метода Харриса: помечены угловые точки.
В качестве примера в табл. 1 представлена матрица смежности для символа, изображенного на рис. 6. Значение «1» на пересечении i-го столбца и j-й строки означает наличие ребра между вершинами pi и pj, «0» – отсутствие ребра между соответствующими вершинами. Программным средством выбрана библиотека OpenCV [2], которая содержит реализацию метода поиска углов по Харрису [10]. На основе метода выделяются угловые точки.
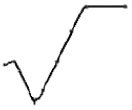
Рис. 6. Узловые точки графа для знака корня
Таблица 1
Матрица смежности вершин графа для знака корня
|
p0 |
p1 |
p2 |
p3 |
p4 |
p5 |
p6 |
p7 |
p8 |
p9 |
p10 |
|
|
p0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
p1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
p2 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
p3 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
p4 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
p5 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
p6 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
|
p7 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
|
p8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
|
p9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
|
p10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
4. Изменение размера изображения
Все изображения с выделенными символами должны быть приведены к одному размеру 32×32. Число 32 выбрано не случайно: во-первых, все изображения, подаваемые на вход сверточной нейронной сети (далее СНС) (о которой будет рассказано ниже), должны быть одного размера, во-вторых, на первом и втором слоях СНС размер карт признаков является целым числом [6]. Входными изображениями являются изображения, полученные после сегментации изображения.
Если размер изображения меньше 32×32, то оно наращивается до 32×32. Далее изображения поступают на блок распознавания.
Распознавание математических символов и букв греческого алфавита с использованием сверточной нейронной сети
1. Архитектура СНС для распознавания греческих букв
СНС – нейронная сеть, имеющая многослойную архитектуру. Слои предназначены для возможности быстрого обучения и уменьшения общего значения функции ошибки [9].
На вход сети и каждого последующего слоя поступают изображения, представленные в виде двумерных массивов. Модель СНС представляет собой последовательность сверточных и вычислительных слоев.
Выбранная в настоящей работе модель сети состоит из пяти слоев: входного, трех скрытых слоев свертки и классификационного выходного. Локальное рецептивное поле сверточных нейронов [9] имеет смещение на два пикселя и размер 5×5. Подробная архитектура сети представлена на рис. 7.
Входными данными нейронной сети являются сегментированные изображения греческих букв из математической формулы. Таким образом, входной слой содержит 1024 нейрона. В эксперименте размер обучающей выборки составил 362 изображения, размер тестирующей выборки – 196 символов.
Второй слой СНС (первый слой свертки) состоит из шести карт признаков размером 14×14. В данном слое находится 14×14×6 = 1176 нейронов. Каждый элемент признаков соединен с рецептивным полем размера 5×5 из входного слоя. Из этого следует, что каждый элемент карты имеет 26 обучаемых весов. Таким образом, в первом сверточном слое находится 1176×26 = 30576 синаптических связей и 156 обучаемых весов. Перейдем к описанию третьего сверточного слоя.
Третий слой, второй слой свертки, состоит из 50 карт признаков размером 5×5 и содержит 5×5×50 = 1250 нейронов. Каждый элемент карты имеет связь с шестью рецептивными полями размером 5×5 из предыдущего слоя. Таким образом, во втором сверточном слое находится 7550 весовых коэффициентов и 188750 синаптических связей. Данные сверточные слои используются для извлечения признаков из изображения. Каждый нейрон соединен со всеми нейронами из предыдущего слоя.
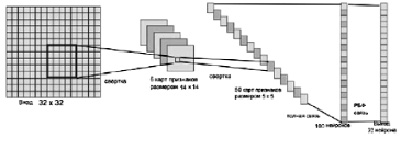
Рис. 7. Архитектура СНС для распознавания букв греческого алфавита
Четвертый слой, открытый, состоит из 100 нейронов. В этом слое содержится 125100 связей и столько же параметров для обучения.
Пятый слой, выходной, состоит из 22 нейронов, так как распознается 22 символа из алфавита. В последнем слое содержится 2222 связей и столько же весов.
Обучение построенной СНС производится с помощью метода обратного распространения ошибки [14]. В данном случае учитывается архитектура сети, а именно то, что веса одной карты признаков используются совместно.
2. Результаты распознавания
Выбранных значений параметров настройки сети оказалось достаточно, чтобы получить довольно высокий процент распознавания. В табл. 2 представлены результаты распознавания тестовой выборки. Табл. 3 демонстрирует точность распознавания обучающей и тестовой выборки.
3. Архитектура СНС для распознавания математических символов
Для распознавания операторов с переменным диапазоном и скобок использовалась СНС с 11 выходными классами. Результаты распознавания символов представлены в табл. 4. Обучающая выборка составила 330 изображений, тестовая – 110. Средняя точность распознавания составила 97,9 %.
Таблица 2
Результаты распознавания букв греческого алфавита
|
Символ |
Процент распознавания |
Символ |
Процент распознавания |
|
|
α |
100 % |
π |
100 % |
|
|
β |
75 % |
ρ |
100 % |
|
|
γ |
100 % |
σ |
100 % |
|
|
δ |
100 % |
ζ |
100 % |
|
|
ε |
100 % |
τ |
100 % |
|
|
ζ |
100 % |
ν |
100 % |
|
|
η |
100 % |
φ |
100 % |
|
|
λ |
100 % |
χ |
88,2353 % |
|
|
μ |
100 % |
ψ |
100 % |
|
|
ν |
100 % |
ω |
100 % |
|
|
ξ |
100 % |
ϕ |
100 % |
Таблица 3
Результат обучения сети
|
Точность распознавания обучающей выборки (362 изображения), % |
Точность распознавания тестовой выборки (196 изображений), % |
Количество эпох обучения |
|
100 |
98,07 |
90 |
Таблица 4
Результат распознавания операторов с переменным диапазоном и скобок
|
Класс |
Процент распознавания |
Класс |
Процент распознавания |
|
|
|
100 |
( |
100 |
|
|
|
100 |
) |
100 |
|
|
|
100 |
{ |
85,7 |
|
|
|
100 |
} |
88,9 |
|
|
|
100 |
Выводы
В статье представлены методы разделения формулы на подформулы с целью изучения структуры формулы и ее упрощенного представления; определены символы, которые выступают в качестве разделителей двух подформул и описаны способы выявления на изображении: знака «=», операторов с переменным диапазоном, линии дроби, скобок. С помощью метода базовых локальных признаков построена модель символа, представлены результаты распознавания букв греческого алфавита, операторов с переменным диапазоном и скобок. Инструментом для распознавания выбрана сверточная нейронная сеть. При этом средняя точность распознавания букв греческого алфавита составила 98,07 %, операторов и скобок – 97,9 %. Цель дальнейших исследований заключается в восстановлении межсимвольных связей и представлении формулы в удобном для пользователя виде.
Рецензенты:
Хачумов В.М., д.т.н., профессор, заведующий лабораторией 0-4 ИСА РАН, г. Москва;
Знаменский С.В., д.ф.-м.н., заведующий лабораторией информатизации образования Институт программных систем им. А.К. Айламазяна РАН, Ярославская обл., Переславский р-н, Веськово.