Важной задачей при проектировании высокооборотных электромеханических преобразователей энергии (ЭМПЭ) с высококоэрцитивными постоянными магнитами (ВПМ) является определение такой формы ВПМ, при которой масса ЭМПЭ будет минимальной, индукция, создаваемая ВПМ в воздушном зазоре, будет максимальной, при этом кривая магнитной индукции будет синусоидальной, а потери энергии в ЭМПЭ при этом будут минимальными [1].
Задачам исследования влияния формы ВПМ ротора ЭМПЭ посвящены работы [2–5], в которых рассматриваются либо роторы коллекторного типа, либо решаются задачи сравнения энергетических характеристик ротора коллекторного типа и ротора с призматическими или цилиндрическими магнитами. При этом решению задачи оптимизации формы ВПМ ротора с призматическими и цилиндрическими ВПМ, намагниченными в диаметральном направлении, практически не уделяется внимания. Хотя последние находят широкое применение в высокооборотных ЭМПЭ [6–8] для децентрализованной энергетики, авиакосмической промышленности и судостроения.
В связи с этим задачей данной работы являются исследования влияния формы ВПМ ротора с призматическими и цилиндрическими магнитами, намагниченными в диаметральном направлении, на характеристики ЭМПЭ.
Решение поставленной задачи осуществляется численными методами с использованием программного пакета Ansoft Maxwell. При этом рассматриваются четыре формы ВПМ ротора (рис. 1 а, г) для высокооборотного ЭМПЭ (частота вращения более 24 000 об/мин).
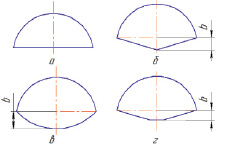
Рис. 1. Исследуемые формы ВПМ ротора
а
б
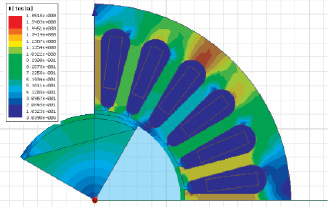
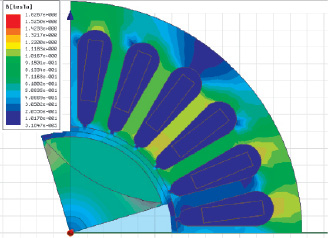
Рис. 2. Спектр распределения магнитной индукции для ВПМ: а – для ВПМ формы по рис. 1а; б – для ВПМ формы по рис. 1в
В результате решения поставленной задачи было получено распределение магнитного поля в воздушном зазоре ЭМПЭ при холостом ходе для каждой рассматриваемой геометрической формы (рис. 2 а, б).
В результате решения поставленной задачи было получено распределение магнитного поля в магнитной цепи ЭМПЭ при холостом ходе для каждой рассматриваемой геометрической формы (рис. 2).
А также были получены зависимости распределения магнитной индукции от величины b (рис. 1), которые были с помощью функций Ansoft Maxwell разложены в ряд Фурье с целью определения их гармонического состава. На рис. 3, 4, 5 представлены зависимости 1, 3 и 5 гармоник для каждой исследуемой формы ВПМ ротора.
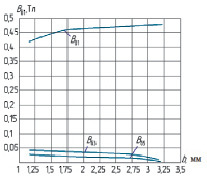
Рис. 3. Зависимость 1, 3 и 5 гармоник для ВПМ формы по рис. 1 г
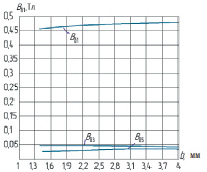
Рис. 4. Зависимость 1, 3 и 5 гармоник для ВПМ формы по рис. 1 б
Из зависимостей, представленных на рис. 3, видно, что с увеличением величины b для исследуемых численных параметров для ВПМ формы по рис. 1 г увеличивается первая гармоническая составляющая (при увеличении величины b с 1,25 до 2,25 первая гармоническая составляющая увеличивается на 8 %), при этом третья и пятая гармонические составляющие снижаются на 3–4 %. Другими словами, при неизменном воздушном зазоре, при применении ВПМ в формы по рис. 1 г можно ожидать увеличение мощности на 17–18 %, а также увеличение КПД ЭМПЭ с ВПМ за счет снижения третьей и пятой гармонических составляющих.
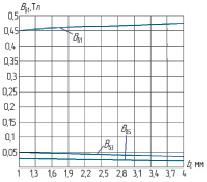
Рис. 5. Зависимость 1, 3 и 5 гармоник для ВПМ формы по рис. 1 в
Важно отметить, что с увеличением расстояния b происходит увеличение массы ВПМ, а следовательно, для высокоскоростных ЭМПЭ и увеличение центробежных сил, действующих на бандажную оболочку ротора, что приведет к увеличению толщины последней, а следовательно, и снижению магнитной индукции в воздушном зазоре. Поэтому для высокоскоростных ЭМПЭ изменение формы ВПМ может оказаться малоэффективным для повышения мощности. В то же время полученные результаты могут являться перспективными для низкоскоростных ЭМПЭ с ВПМ, применяемых, к примеру, в ветро- и гидроэнергетике.
Из зависимостей, представленных на рис. 4, видно, что с увеличением величины b для исследуемых численных параметров для ВПМ формы по рис. 1 б увеличивается первая гармоническая составляющая (при увеличении величины b с 1,6 до 3,2 первая гармоническая составляющая увеличивается на 3–3,5 %) при этом третья гармоническая составляющая снижается на 2–3 %. При этом пятая гармоническая составляющая незначительно увеличивается. Другими словами, при неизменном воздушном зазоре, при применении ВПМ в формы по рис. 1 б можно ожидать увеличение мощности на 7–8 %, а также увеличение КПД ЭМПЭ с ВПМ за счет снижения третьей гармонической составляющей.
Таким образом, форма ВПМ по рис. 1 б менее эффективна по сравнению с формой ВПМ по рис. 1 г по энергетическим характеристикам.
Из зависимостей, представленных на рис. 5 видно, что с увеличением величины b для исследуемых численных параметров для ВПМ формы по рис. 1 в увеличивается первая гармоническая составляющая (при увеличении величины b с 1,25 до 2,25 первая гармоническая составляющая увеличивается на 4 %), при этом третья гармоническая составляющая снижается на 2–3 %. При этом 5 гармоническая составляющая незначительно снижается на 0,5–1 %. Другими словами, при неизменном воздушном зазоре, при применении ВПМ в формы по рис. 1 г можно ожидать увеличение мощности на 8–9 %, а также увеличение КПД ЭМПЭ с ВПМ за счет снижения третьей гармонической составляющей.
Таким образом, из рассмотренных форм ВПМ можно сделать вывод об эффективности формы ВПМ по рис. 1 г. Причем наибольшую эффективность данная форма будет иметь при применении в низкоскоростных ЭМПЭ. Так как при применении данной формы в высокоскоростных ЭМПЭ с ВПМ при увеличении величины b вызовет увеличение толщины бандажной оболочки ротора.
Представленные результаты могут быть использованы на практике при проектировании ЭМПЭ с ВПМ.
Рецензенты:
Демин А.Ю., д.т.н., профессор кафедры электроники и биомедицинских технологий, ФГБОУ ВПО «Уфимский государственный авиационный технический университет», г. Уфа;
Фетисов В.С., д.т.н., профессор кафедры информационно-измерительной техники, ФГБОУ ВПО «Уфимский государственный авиационный технический университет», г. Уфа.



